Exactly! The frontier labs have the compute and incentive to push capabilities forward, while randos on lesswrong are instead more likely to study alignment in weak open source models

Exactly

The universe doesn't care if you try to hide your oh so secret insights; multiple frontier labs are working on those insights

The only people who care are the people here getting more doomy and having worse norms for conversations.

I don't appreciate the local discourse norm of "let's not mention the scary ideas but rest assured they're very very scary". It's not healthy. If you explained the idea, we could shoot it down! But if it's scary and hidden then we can't.

Also, multiple frontier labs are currently working on it and you think your lesswrong comment is going to make a difference?

You should at least say by when you will consider this specific single breakthrough thing to be falsified.

You should show your calculation or your code, including all the data and parameter choices. Otherwise I can't evaluate this.

I assume you're picking parameters to exaggerate the effects, because just from the exaggerations you've already conceded (0.9/0.6 shouldn't be squared and attenuation to get direct effects should be 0.824), you've already exaggerated the results by a factor of sqrt(0.9/0.6)/0.824 for editing, which is around a 50% overestimate.

I don't think that was deliberate on your part, but I think wishful thinking and the desire to paint a compelling story (and get funding) is causing you to be biased in what you adjust for and in which mistakes you catch. It's natural in your position to scrutinize low estimates but not high ones. So to trust your numbers I'd need to understand how you got them.

I don't understand. Can you explain how you're inferring the SNP effect sizes?

I'm talking about this graph:

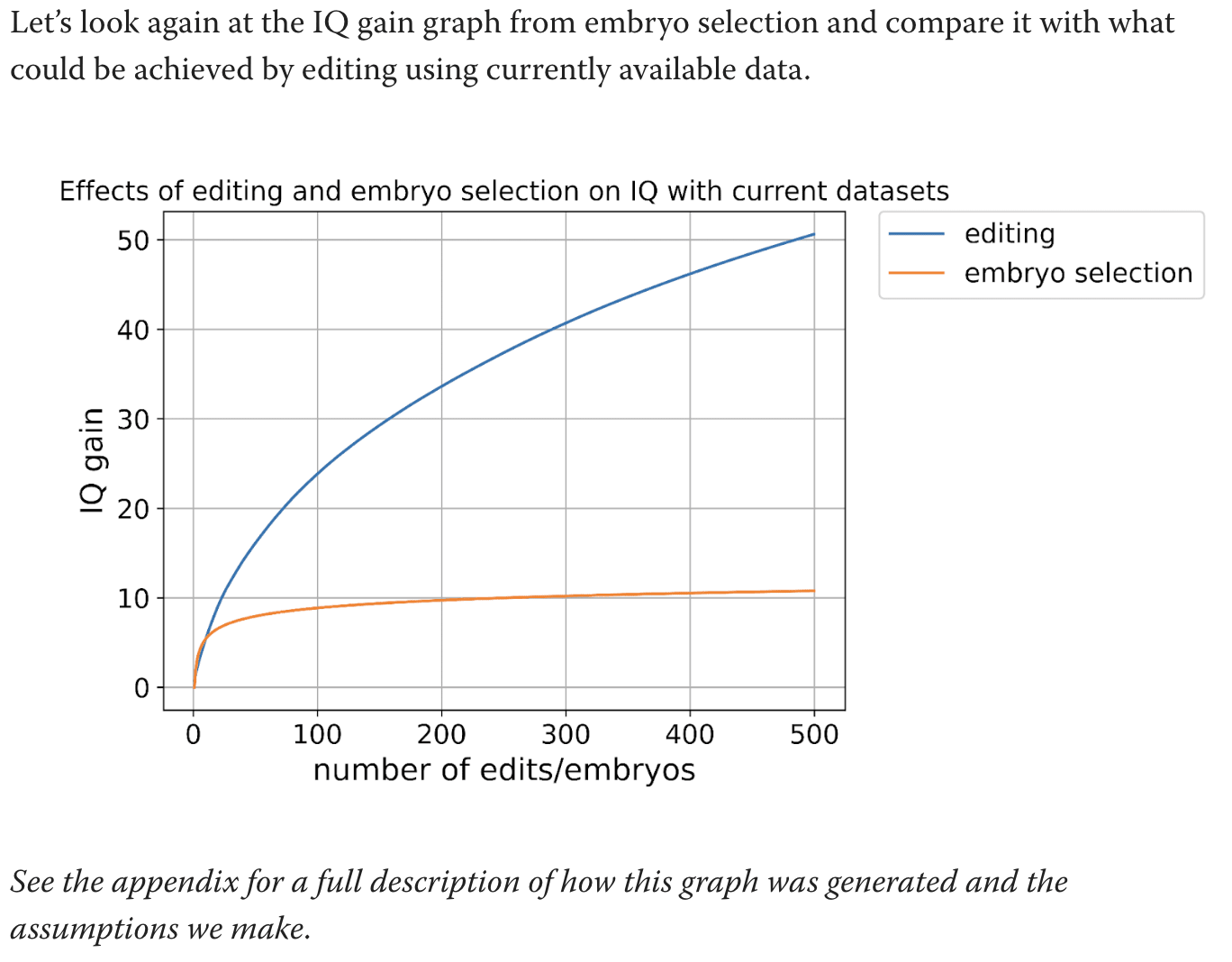
What are the calculations used for this graph. Text says to see the appendix but the appendix does not actually explain how you got this graph.

You're mixing up h^2 estimates with predictor R^2 performance. It's possible to get an estimate of h^2 with much less statistical power than it takes to build a predictor that good.

Thanks. I understand now. But isn't the R^2 the relevant measure? You don't know which genes to edit to get the h^2 number (nor do you know what to select on). You're doing the calculation 0.2*(0.9/0.6)^2 when the relevant calculation is something like 0.05*(0.9/0.6). Off by a factor of 6 for the power of selection, or sqrt(6)=2.45 for the power of editing

The paper you called largest ever GWAS gave a direct h^2 estimate of 0.05 for cognitive performance. How are these papers getting 0.2? I don't understand what they're doing. Some type of meta analysis?

The test-retest reliability you linked has different reliabilities for different subtests. The correct adjustment depends on which subtests are being used. If cognitive performance is some kind of sumscore of the subtests, its reliability would be higher than for the individual subtests.

Also, I don't think the calculation 0.2*(0.9/0.6)^2 is the correct adjustment. A test-retest correlation is already essentially the square of a correlation of the test with an underlying latent factor (both the test AND the retest have error). E.g. if a test T can be written as

T=aX+sqrt(1-a)E

where X is ability and E is error (all with standard deviation 1 and the error independent of the ability), then a correlation of T with a resample of T (with new independent error but same ability) would be a^2. But the adjustment to h^2 should be proportional to a^2, so it should be proportional to the test-retest correlation, not the square of the test-retest correlation. Am I getting this wrong?

Thanks! I understand their numbers a bit better, then. Still, direct effects of cognitive performance explain 5% of variance. Can't multiply the variance explained of EA by the attenuation of cognitive performance! 

Do you have evidence for direct effects of either one of them being higher than 5% of variance?

I don't quite understand your numbers in the OP but it feels like you're inflating them substantially. Is the full calculation somewhere?

You should decide whether you're using a GWAS on cognitive performance or on educational attainment (EA). This paper you linked is using a GWAS for EA, and finding that very little of the predictive power was direct effects. Exactly the opposite of your claim:

For predicting EA, the ratio of direct to population effect estimates is 0.556 (s.e. = 0.020), implying that 100% × 0.556² = 30.9% of the PGI’s R² is due to its direct effect. 

Then they compare this to cognitive performance. For cognitive performance, the ratio was better, but it's not 0.824, it's ${0.824}^2=0.68$. But actually, even this is possibly too high: the table in figure 4 has a ratio that looks much smaller than this, and refers to supplementary table 10 for numbers. I checked supplementary table 10, and it says that the "direct-population ratio" is 0.656, not 0.824. So quite possibly the right value is ${0.656}^2=0.43$ even for cognitive performance.

Why is the cognitive performance number bigger? Well, it's possibly because there's less data on cognitive performance, so the estimates are based on more obvious or easy-to-find effects. The final, predictive power of the direct effects for EA and for cognitive performance is similar, around 3% of the variance, if I'm reading it correctly (not sure about this). So the ratios are somewhat different, but the population GWAS predictive power is also somewhat different in the opposite direction, and these mostly cancel out.