After adding “from California”, the 7b model responds instead with the incorrect answer “Bay”.
That behavior makes no sense to me (other than that 'Bay' and 'California' are related concepts, so their embeddings presumably have some inner-product). Which supports your claim that the word-suppression mechanism's implementation in Llama-7B is an incoherent mess. What I'm wondering is if the one in LLama-70B, while doubtless larger, might be more sensibly designed and thus actually easier to interpret.
We also need to bear in mind that your game, of giving. a one word answer when one value is forbidden, is (designed to be) very simple in its effects on tokens, but the model probably hasn't seen it often before. So the mechanism you're interpreting is probably intended for implementing more complex behaviors, perhaps along the lines of "certain words and phrases aren't allowed to be used in certain circumstances, but you still have to make sense". So a certain amount of complexity in its implementation, including overlap with "similar" words, seems unsurprising. Also, forbidding "California" is a really odd thing to do, might the mechanism work better if you forbade a word closer to things that are often forbidden in some contexts?
Our best guess is that "Bay" is the second-most-likely answer (after "California") to the factual recall question "The Golden Gate Bridge is in the state of ". Indeed, when running our own version of Llama-2-7b-chat, adding "from California" results in "San Francisco" being outputted instead of "Bay". As you can see in this notebook, "San Francisco" is the second-most-likely answer for our setup. replicate.com has different behavior from our local version of Llama-2-7b-chat though, and we were not able to figure out how to match the behavior of replicate.com.
The second-most-likely theory is also not perfect, since it is possible to attack the replicate model to output "San Francisco", e.g. if you forbid "cat": https://replicate.com/p/q3qixwdbm6egjmaan3fjfbhywe.
Re your second point: the circuit in Llama-2-70b-chat is not obviously larger than the one in Llama-2-7b-chat. In our paper, we measured 7b to have 35 suppressive components, while 70b has 34 suppressive components. However, since we weren't able to find attacks for 70b, it may be true that its components are cleaner. Part of the reason we weren't able to find an attack for 70b is that it is much more annoying to work with,(e.g. it requires multiple A100 GPUs to run and it doesn't have great support in TransformLens).
Finally, good point about our game being kind of unnatural. My personal take is that the majority of things we are currently asking our LLMs to do are "unnatural" (since they require a large amount of generalization from the training set). This ultimately is an empirical question, and I think an interesting avenue for future work.
Specifically, I am curious if there are good automated ways of lower-bounding the complexity of circuits. It is impossible to do this well in general (c.f. Kolmogorov complexity being uncomputable), but maybe there are good heuristics that work well in practice. Our first-order-patching method is one such heuristic, but it is lacking in the sense that it does not say how interpretable each component is. Perhaps if techniques like AC/DC or subnetwork probing are improved, they could give a better sense of circuit complexity.
You could of course quantize Llama-2-70b to work with it inside a single A100 80GB, say to 6 or 8 bits, but that's obviously going to apply some fuzz to everything, and probably isn't something you want to have to footnote in an academic paper. Still, for finding an attack, you could find it in a 6-bit quantized version and then confirm it works against the full model.
I'm not sure you need to worry that much about uncomputibility in something with less than 50 layers, but I suppose circuits can get quite large in practice. My hunch is that this particular one actually extends from about layer 16 (midpoint of the model) to about 20-21 (where the big jumps in divergence between refusal and answering happen: I'd guess that's a "final decision").
Kudos on the well-written paper and post!
A key question is whether behaviors of interest in these large scale settings are tractable to study.
We provide some evidence in the negative, and show that even simple word suppression in Llama-2 may be computationally irreducible. Our evidence is the existence of adversarial examples for the word suppression behavior.
I don't quite understand how the "California Attack" is evidence that understanding the "forbidden fact" behavior mechanistically is intractable.
In fact, it seems like the opposite to me. At the end of section 3 of the paper, you examine attention patterns of suppressor heads and find that they exhibit "key semantic specificity, ... [privileging] correct answers to the factual recall over all other keys" (rather than privileging the forbidden word, as one would expect). The "California Attack" then comes out of this mechanistic insight - the mechanistic understanding of suppressor head attention patterns informs the adversarial attack, and predicts the resulting behavior. This seems like the opposite of computational irreducibility to me!
The attention analysis and the attack both serve as good evidence that the model uses this heuristic. Faulty or not, this is a heuristic that the model uses, and knowing this gives us insight into understanding how the model is (imperfectly) performing the task mechanistically.
Glad you enjoyed the work and thank you for the comment! Here are my thoughts on what you wrote:
I don't quite understand how the "California Attack" is evidence that understanding the "forbidden fact" behavior mechanistically is intractable.
This depends on your definition of "understanding" and your definition of "tractable". If we take "understanding" to mean the ability to predict some non-trivial aspects of behavior, then you are entirely correct that approaches like mech-interp are tractable, since in our case is was mechanistic analysis that led us to predict and subsequently discover the California Attack[1].
However, if we define "understanding" as "having a faithful[2] description of behavior to the level of always accurately predicting the most-likely next token" and "tractability" as "the description fitting within a 100 page arXiv paper", then I would say that the California Attack is evidence that understanding the "forbidden fact" behavior is intractable. This is because the California Attack is actually quite finicky -- sometimes it works and sometimes it doesn't, and I don't believe one can fit in 100 pages the rule that determines all the cases in which it works and all the cases in which it doesn't.
Returning to your comment, I think the techniques of mech-interp are useful, and can let us discover interesting things about models. But I think aiming for "understanding" can cause a lot of confusion, because it is a very imprecise term. Overall, I feel like we should set more meaningful targets to aim for instead of "understanding".
- ^
Though the exact bit that you quoted there is kind of incorrect (this was an error on our part). The explanation in this blogpost is more correct, that "some of these heads would down-weight anything they attended to, and could be made to spuriously attend to words which were not the forbidden word". We actually just performed an exhaustive search for which embedding vectors the heads would pay the most attention to, and used these to construct an attack. We have since amended in the newest version of the paper (just updated yesterday) to reflect this.
- ^
By faithfulness, I mean a description that matches the actual behavior of the phenomena. This is similar to the definition given in arxiv.org/abs/2211.00593. This is also not a very precisely defined term, because there is wiggle room. For example, is the float16 version of a network a faithful description of the float32 version of the network? For AI safety purposes, I feel like faithfulness should at least capture behaviors like the California Attack and phenomena like jailbreaks and prompt injections.
What is a Waluigi component? A component that always says a fact, even when there is training to refuse facts in certain cases...?
The Waluigi Effect is defined by Cleo Nardo as follows:
The Waluigi Effect: After you train an LLM to satisfy a desirable property , then it's easier to elicit the chatbot into satisfying the exact opposite of property .
For our project, we prompted Llama-2-chat models to satisfy the property that they would downweight the correct answer when forbidden from saying it. We found that 35 residual stream components were necessary to explain the models average tendency to do .
However, in addition to these 35 suppressive components, there were also some components which demonstrated a promotive effect. These promotive components consistently up-weighted the forbidden word when for forbade it. We called these components "Waluigi components" because they acted against the instructions in the prompt.
Wherever the Waluigi effect holds, one should expect such "Waluigi components" to exist.
See the following plots for what I mean by suppressive and promotive heads (I just generated these, they are not in the paper):
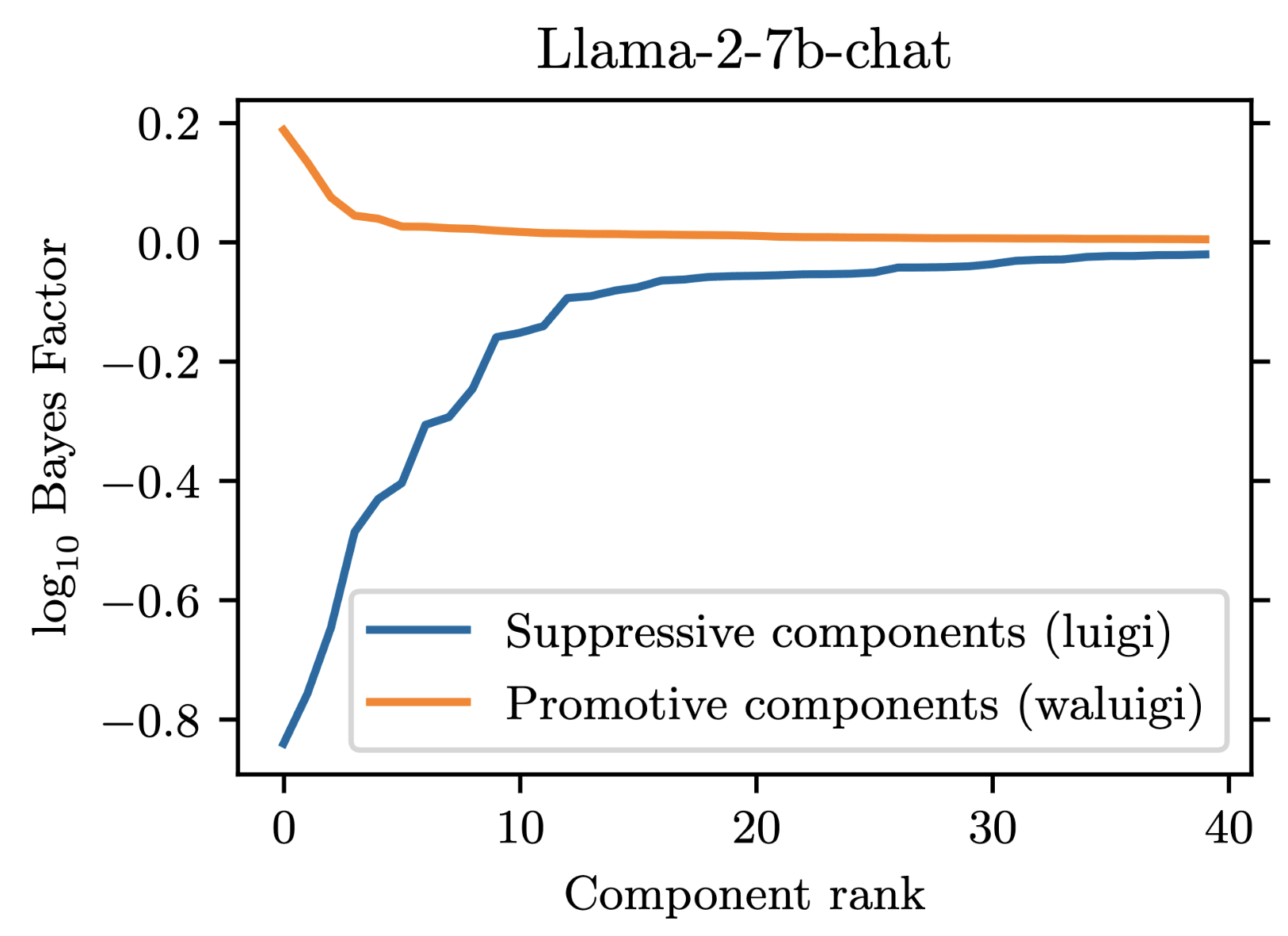
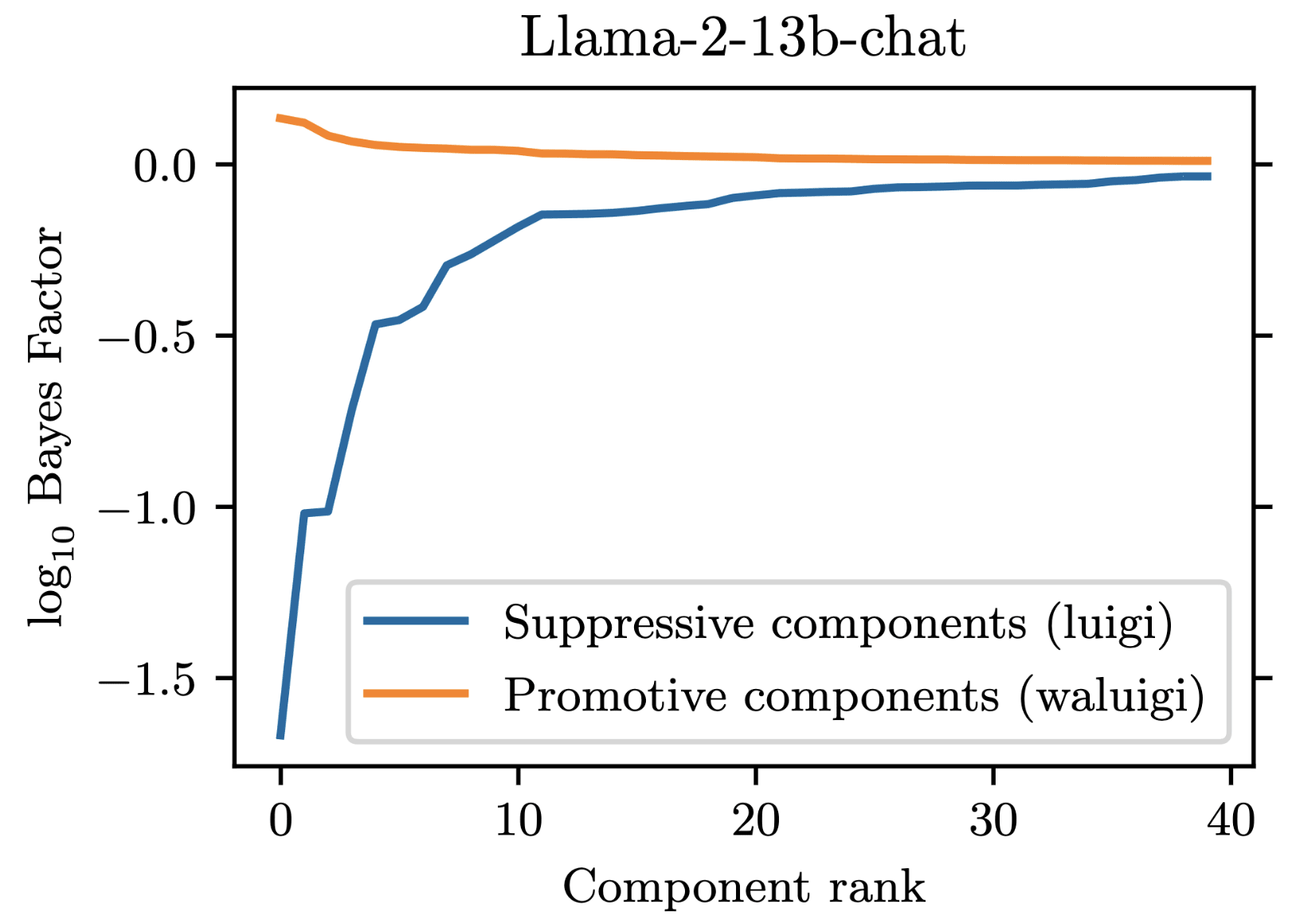
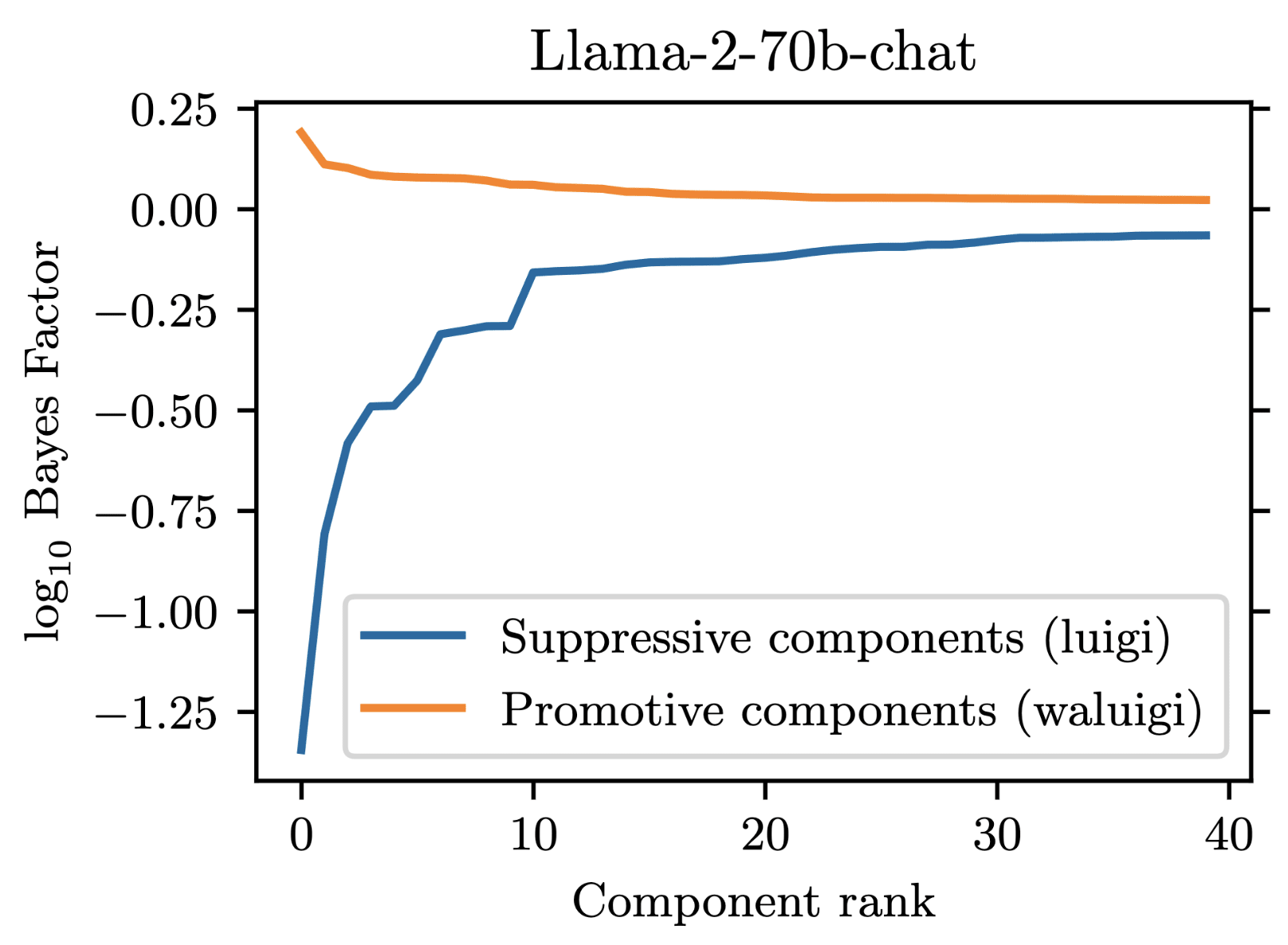
Thanks!
In general after the Copy Suppression paper (https://arxiv.org/pdf/2310.04625.pdf) I'm hesitant to call this a Waluigi component -- in that work we found that "Negative IOI Heads" and "Anti-Induction Heads" are not specifically about IOI or Induction at all, they're just doing meta-processing to calibrate outputs.
Similarly, it seems possible the Waluigi components are just making the forbidden tokens appear with prob 10^{-3} rather than 10^{-5} or something like that, and would be incapable of actually making the harmful completion likely
Overview
We tried to understand at a circuit level how Llama-2 models perform a simple task: not replying with a word when told not to. We mostly failed at fully reverse engineering the responsible circuit, but in the process we learned a few things about mechanistic interpretability. We share our takeaways here, which we hope are useful to other researchers. We are very interested in critiques of our views.
Our major takeaways:
More minor takeaways:
More technical details are available in our paper, which serves as the appendix to this post.
Project motivation
When large language models (LLMs) predict the next token, they often need to reconcile competing objectives. For example, many models are RLHF’d to be helpful and harmless, and these objectives come into conflict when users ask dangerous queries. Ideally, we want to be able to control which objective wins out. For instance, Asimov’s Three Laws of Robotics codifies that harmlessness should always win over helpfulness. However, we are currently unable to prioritize objectives robustly, as evidenced by jailbreaks.
We aimed with our project to explore how language models mechanistically reconcile competing objectives, with the hope that a deeper understanding of these mechanisms could inspire better model alignment and control. Specifically, we tried to understand how Llama-2 models reconcile obedience and truthfulness in the context of prompts like the following one:
Here the obedience objective makes the model not want to respond with “California”, while the truthfulness objective does the opposite. We refer to this as a competing prompt since the correct answer is forbidden (a non-competing prompt forbids an incorrect answer). Since there has already been some work on how large language models perform factual recall [1, 2, 3, 4, 5, 6], we decided to focus on the obedience objective, and in particular on what mechanisms the model uses to downweight the forbidden word.
We found that compared to forbidding an incorrect answer, forbidding the correct answer causes Llama-2 to decrease its odds of answering correctly by a factor of over 1000x on average [1]. This suppressive effect is what we attempted to reverse engineer.
Reverse engineering results
We performed our reverse engineering by working backwards. To start, we noted that the next token distribution of Llama-2 conditioned on a prompt string s can be written as
next_token_distribution(s)=Softmax(WU⋅LayerNorm( ∑iri(s))),where each ri:Prompt→Rdmodel denotes a residual stream component at the last token position of s, and where WU∈Rdvocab×dmodel is the unembedding matrix of Llama-2.
Any circuit that the model uses to suppress the correct answer must eventually act through the ri components. Thus we began our reverse engineering by trying to identify the ri components directly responsible for suppression. To measure the suppressive effect of a component ri, we compute the average amount it decreases the probability of the correct answer. We did this using a technique called first-order patching [2], and we measured probability decrease as a log Bayes factor (Takeaway 3).
In llama-2-7b-chat, there are 1057 residual stream components: 1 initial embedding component, 1024 attention head components (32 heads per layer over 32 layers), and 32 MLP head components (one per layer). We found that out of these, 35 components were responsible for the suppression effect. Here is a plot demonstrating this:
At minimum then, we would need to explain 35 different components in order to fully reverse-engineer the circuit. 7 / 35 of these components were MLPs, which we chose not to prioritize due to lack of previous work on reverse engineering MLPs. The remaining 28 / 35 components were attention heads, and had fairly heterogeneous behavior, differing in both their attention patterns and OV-circuit behaviors.
At this point, we shifted our focus to explaining the behavior of the most important attention heads. However, we discovered that even the attention heads with the strongest suppression effects seemed to use faulty heuristics that (considered alone) did not reliably execute the suppression behavior (see California Attack).
At this point, we felt there was no way we were going to get a full description of the entire suppression circuit. Thus, we concluded the project and submitted a workshop paper. Our failure got us thinking however: What if certain aspects of language models are just fundamentally uninterpretable?
Takeaway 1: Computational Irreducibility
Mechanistic interpretability attempts to faithfully explain model behavior in simple ways. But what if there are model behaviors that have no simple explanations?
This is the premise behind computational irreducibility: the idea that there are systems whose behavior can only be predicted by fully simulating the system itself. Initially proposed by Stephen Wolfram in the context of cellular automata, computational irreducibility challenges the efficacy of reductionism — the “bottom-up” philosophy behind mechanistic interpretability. Indeed, Wolfram recently made this comment during a TED talk:
Even computationally irreducible systems can have sub-behaviors that are efficiently predictable though. Simply observing computational irreducibility in some behavior does not, by itself, doom mechanistic interpretability. Nonetheless, previous work in mech. interp has largely studied quasi-algorithmic tasks or small models. Moving away from understanding toy settings to understanding models with trillions of parameters will be much harder. A key question is whether behaviors of interest in these large scale settings are tractable to study.
We provide some evidence in the negative, and show that even simple word suppression in Llama-2 may be computationally irreducible. Our evidence is the existence of adversarial examples for the word suppression behavior.
An interpretability-inspired adversarial attack: The California Attack
In our attempt to reverse-engineer the attention head components responsible for suppression, we discovered that these heads were operating on faulty heuristics. In particular, some of these heads would down-weight anything they attended to, and could be made to spuriously attend to words which were not the forbidden word. By exploiting this effect, we manually constructed adversarial prompts on which the model would spuriously answer incorrectly.
Here is a canonical example of our attack in action. Consider the following prompt:
On this base prompt, llama-2-7b-chat correctly responds with the answer “California”. However, we can add two innocuous words to the system prompt to create an adversarial prompt:
After adding “from California”, the 7b model responds instead with the incorrect answer “Bay”.[3] This was the first clean adversarial attack we came up with, hence the name “California Attack”.
What the California Attack reveals is that the forbidden word suppression behavior in Llama-2 is actually quite complicated, and has a lot of idiosyncratic quirks. Faithful explanations of the forbidden word suppression behavior must include a sense of where these quirks come from, so it seems unlikely that there exists a simple faithful explanation of the suppression behavior. This aligns with growing evidence that LLMs have incredibly rich inner mechanisms that are beyond the scope of current tools [1, 2].
How should interp researchers deal with computational irreducibility?
What can we do in light of the possibility that certain behaviors may be uninterpretable? This is a tricky question, as even when there is suggestive evidence that a behavior is hard to fully interpret, it is notoriously difficult to prove that it is irreducible (doing so is roughly equivalent to computing the Kolmogorov complexity of that behavior).
However, we think it is important to keep in mind that some behaviors might be irreducible even if one can’t prove that to be the case. For an irreducible property, no amount of time, effort, and compute can overcome its fundamental intractability. Thus, if progress is stalling with current methodology, researchers should be ready to pivot to new problems and frameworks for thinking about models.
This section is a conjecture. Its purpose is not to dismiss mechanistic interpretability, but rather to raise potential concerns. One piece of evidence against computational irreducibility posing an issue is that we could not find a California Attack for Llama-2-70b-chat, ChatGPT-3.5, and ChatGPT-4 [4]. Bigger models seem more capable and more robust to exploits like the California Attack, which may suggest that they use cleaner circuits to implement behaviors.
In conclusion, computational irreducibility implies mechanistic interpretability cannot yield insights into all behaviors. Thus, it is important to choose the right behaviors to study.
Takeaway 2: “Understanding” should not be a terminal goal of interpretability research
Motivating understanding
Let’s say one day, an OpenMind researcher says to you that they have a full mechanistic explanation for how their frontier LLM works. You are doubtful, so you test them: “Okay, then can you explain why <jailbreak x> gets your LLM to output <bad response>?”
The researcher responds: “You see, when you feed in <jailbreak x> to our LLM, the text first gets tokenized, and then turned into embedding vectors, and then gets fed into the a transformer block, where it first gets hit by the KQV circuit [...] to produce <bad response>!”
You are not impressed, and respond: “That’s not a mechanistic explanation. You just described to me how a transformer works. You haven’t told me anything about how how your LLM is reasoning about the jailbreak!”
The employee quickly retorts: “Ah but we know precisely how our LLM is reasoning about the jailbreak. We can trace every single intermediate computation and describe exactly how they are routed and get combined to produce the final answer! What more could you want?”
This story poses a common and confusing question: What does it mean for something to be human-understandable?
The understanding trap
Throughout this project, we repeatedly asked ourselves what good mechanistic interpretability research looks like. At first, we thought it was research that manages to fully reverse-engineer models, explaining their function in human-understandable ways. Under this frame, we failed. But it was also difficult to pinpoint our exact failures. Thinking about things more, we realized much of our confusion was due to “understanding” being an ill-defined notion.
We now believe that judging interpretability research using the frame of “understanding” can be a trap. Fundamentally, “understanding” is a very subjective term, and an explanation that is understandable for one person may not be for another (consider the OpenMind researcher). We believe that for AI safety research, “understanding” should not be a terminal goal. Rather, “understanding” should be an instrumental tool used to achieve other ends.
It’s also easy to get caught up in creating a principled notion of understanding. But as long as understanding is regarded as the end goal, researchers can easily get trapped in using methods that look nice to humans over being useful, resulting in “streetlight” interpretability and cherrypicked results. This might mean techniques won’t scale to bigger models — which is the setting we care the most about.
Thus, we believe the right response to the OpenMind researcher is as follows: “Mechanistic explanations are valuable insofar as they help safely develop and deploy AI. You might have a full mechanistic explanation, but it doesn’t help assure me that your AI is aligned or safe.”
As mechanistic interpretability matures as a field, researchers should target use cases for their work. For example, before undertaking a project, researchers could set terminal goals and update them as work progresses. This would also make it more likely that interpretability breakthroughs achieve safety goals over capabilities advances. We realize that we have not provided a particularly precise razor for determining what mechanistic interpretability research is worth doing: it is our hope that the field of mechanistic interpretability develops a clearer sense of this as it develops.
Lastly, it is hard to predict exactly what advances will come from more “basic”, less back-chained interpretability. This tension between working on what is “interesting” and working on what is “important” is ultimately up to the individual to reconcile.
Minor takeaways
Finally we also had some important but more minor takeaways.
Takeaway 3: Log-odds is a great metric
We chose to represent probabilities in terms of log-odds and to compare probabilities using log Bayes factors. Log-odds is not a standard-unit of measurement in interpretability work, but we believe that it has unique advantages when it comes to interpretability work on language models.
Probability differences and log-probability differences of output tokens are common metrics for measuring the effect size of activation patching in language models (Zhang et al. 2023). But both have drawbacks:
Being sensitive to the upper and lower tails is important statistically. Moreover, being insensitive can mean failing to capture the mechanistic behavior of an LLM: A token prediction probability changing from 99% to 99.9999% corresponds to a large difference in output logits, which necessarily reflects a large difference in intermediate activations.
Log-odds-ratios (or log-odds) fix this issue. Given a probability p, its associated log-odds is given by the quantity logit(p)=log(p/(1−p)). And given two probabilities p1 and p2 the log Bayes factor needed to transform p1 into p2 is given by logit(p2)−logit(p1).
These measures have a few nice properties (see Appendix D for full details and derivations):
Now suppose someone tells you some news X, and you know that in worlds where E occurs, the probability you would have gotten this news is a, and in worlds where E does not occur, the probability you would have gotten this news is b.
If you are a good Bayesian, you would revise your belief with Bayes' rule. This would result in your belief in the probability of E increasing additively by a log Bayes factor of logab.
Moreover, if you receive multiple independent pieces of news X1,…,Xn, which each individually would have resulted in a log Bayes factor update of δ1,…,δn, then the net effect of receiving all this news is that your log-odds of E increases by δ1+⋯+δn.
We show in our paper (Appendix D) that our residual stream components act somewhat independently, illustrating that this Bayesian interpretation is partially valid.
Takeaway 4: Tooling is important and should not be taken for granted (or how we discovered our Llamas were concussed)
We used the amazing open-source TransformerLens library to study the Llama-2 model series. TransformerLens converts HuggingFace models into
HookedTransformerobjects, which allows users to more easily store and manipulate intermediate activations.However, we discovered late into our project that the conversion procedure for Llama-2 models was subtlety broken. Basically, the
HookedTransformerLlama-2 models were concussed: it was not evident from their outputs that their implementation was wrong, as they still behaved coherently, but the output logits ofHookedTransformermodels differed significantly from the output logits of the base HuggingFace models.Luckily for us, this issue turned out to not be a big deal, as rerunning with fixed code returned essentially the same results. However, this easily could have not been the case.
Thus one important takeaway for us is to not take tooling reliability for granted. This is particularly true for mechanistic interpretability, a new and relatively small field, where there are not thousands of researchers to stress-test libraries. Our recommendation here is to try and always have comparisons with known baselines (e.g. HuggingFace models).
See Section 1 of our paper for details.
A particular type of path-patching. See Section 2 of our paper for more details.
This attack also works on llama-2-13b-chat, but we couldn’t find a corresponding one for 70b (although we did not make a concerted effort to do so). We were able to design other similar prompts for 7b and 13b that exploited their messy heuristics. These attacks are quite finicky. For example, they show different behavior when running on our own machines vs. on replicate.com, possibly due to slight differences in prompt construction.
Though for all three of these models, we did not look closely at model internals. In the case of ChatGPT-3.5 and ChatGPT-4, this was because the model was closed-source. In the case of llama-2-70b-chat, this was because TransformerLens had limited support for the model due to its large memory footprint.