Thanks for sharing! Writing up negative results is a valuable thing for the community that often gets skipped, thanks for putting in the effort
Very cool and well-presented - thanks for taking the time to write this down. I thought about this question at some point and ended up deciding that the compressed sensing picture isn't very well shaped for this, but didn't have a complete argument for this - it's nice to have confirmation
Thank you for writing this up! I experimented briefly with group sparsity as well, but with the goal of learning the "hierarchy" of features rather than to learn circular features like you're doing here. I also struggled to get it to work in toy settings, but didn't try extensively and ended up moving on to other things. I still think there must be something in group sparsity, since it's so well studied in sparse coding and clearly does work in theory.
I also struggled with the problem of how to choose groups, since for traditional group sparsity you need to set the groups before-hand. I like your idea of trying to learn the group space. For using group sparsity to recover hierarchy, I wonder if there's a way to learn a direction for the group as a whole, and project out that direction from each member of the group. The idea would be that if latents are sharing common components, those common components should probably be their own "group" representation, and this should be done until the leaf nodes are mostly orthogonal to each other. There are definitely overlapping hierarchies too, which is a challenge.
Regardless, thank you for sharing this! There's a lot of great ideas in this post.
Introduction
Soon after we released Not All Language Model Features Are One-Dimensionally Linear, I started working with @Logan Riggs and @Jannik Brinkmann on a natural followup to the paper: could we build a variant of SAEs that could find multi-dimensional features directly, instead of needing to cluster SAE latents post-hoc like we did in the paper.
We worked on this for a few months last summer and tried a bunch of things. Unfortunately, none of our results were that compelling, and eventually our interest in the project died down and we didn’t publish our (mostly negative) results. Recently, multiple people (@Noa Nabeshima , @chanind, Goncalo Paulo) said they were interested in working on SAEs that could find multi-dimensional features, so I decided I would write up what we tried.
At this point the results are almost a year old, but I think the overall narrative should still be correct. This document contains my results from the project; Logan had some additional results about circuits, and Jannik tried some additional things with learned groups, but I am not confident I can describe those as well so long afterwards.
With the benefit of hindsight, I have some concerns with this research direction:
I think that it’s possible that a good idea exists somewhere in this area, but I’m not sure I would recommend this direction to anyone unless you have an intuition for where that good idea lies.
Group SAEs
Group SAEs have been previously studied in the dictionary learning literature. The idea is to try to modify the L1 sparsity penalty such that groups of latents are encouraged to span meaningful subspaces in model activations (like the subspace of representations for a digit from MNIST or a concept from imagenet). We mostly use the approach outlined in this paper, the ℓ1/ℓ2 norm. This is like a normal SAE, but for the sparsity penalty you split the latents into equal sized groups and then take the L2 of each group’s activations, followed by taking the L1 (sum) of the L2s. The intuition is that if two latents in the same group fire, they are penalized less than if two latents in different groups fire. The authors show that this works for MNIST and imagenet.
Synthetic Circles Experiments
We first tried training Group SAEs on a synthetic dataset of multi-dimensional representations. The dataset combines 1600 circles in 200 dimensional space in superposition. Each circle (really an ellipse) consists of two random unit vectors a, b in 200D space with points acos(theta) + bsin(theta). Each datapoint in the dataset is generated by 3 steps:
We trained two normal SAEs on this synthetic dataset with width = 1600 * 8 and 1600 * 16. Using a naive solution, the SAE should require 4 vectors per circle since activations can't be negative. We find that the SAE successfully finds the circles (we quantify this by if decoder vectors projected into the plane lose less than 0.01 of their magnitude) and L0 is around optimal, although the MSE is mediocre (~0.5 of variance recovered). We can then plot the SAE vectors “belonging” to each plane (the recovery of each circle is quantified by passing random points on it through the SAE and looking at variance explained):
One interesting thing is that we see pretty clear feature splitting between the two SAEs. Below, we plot the learned decoder vectors corresponding to the first circle plane for each SAE, as well as the histogram showing the number of decoder vectors per circle plane for each SAE. Both show that the bigger SAE has learned about twice as many decoder vectors per plane as the smaller SAE.
Ideally, any good grouped SAE should avoid this feature splitting on this synthetic dataset (so the histogram should have a maximum at 4 features, which is the minimum needed to represent each circle plane).
We also tried training grouped SAEs of size 2 on this synthetic data. Our first attempt worked to the extent that each group learned features in the same ground truth circle plane, but had a few problems. The first was that each group learned two copies of the same vector (since this reduces the L2) and then there were just multiple groups per plane, exactly like the normal SAE. We fixed this by adding a loss term for the Relu of the pairwise within-group dot product (excluding self-dots), which worked nicely to make each group's vectors perpendicular. At times we also added a threshold. Another problem was that multiple groups were learned per plane, which we never really solved.
Training Group SAEs on GPT-2
The next thing we tried was training Group SAEs on layer 7 GPT-2 activations.
High level metrics
We found that some high level metrics seemed to improve when compared to ReLU SAEs (although ReLU SAEs are far from SOTA nowadays). At the same sparsity, the explained variance and CE loss score for the group SAEs was a little bit higher than a ReLU SAE. It’s actually not really clear if this is even desired or expected, but it’s interesting to see! There was also some evidence that there was less feature splitting because the max intra-cosine sims were lower, although we also had high feature duplication so it’s hard to draw too much from this.
Overall, the group SAE overall seemed to work, in that the groups were semantically related: the Jaccard similarity between the two latents in many groups of the group SAE was very high.
Looking at some actual examples by examining the plane of representations from the group, some seemed somewhat interpretable, but there didn’t seem to be incredibly interesting multi-dimensional structure (and indeed, training a normal SAE and then clustering certainly might have found these examples as well).
Do the Group SAEs Capture Known Circular Subspaces
We also looked at how well the circular days of the week and months of the year subspaces were captured by the Group SAEs; did the SAE learn a bunch of size 2 groups to reconstruct those circular planes?
First, I took sentences from the Pile ending in a month of the year token and got the layer 7 GPT-2 activations. Then, I took the top 25 layer 7 SAE features that activated on these examples. Ablating the reconstruction to only these, there was a circle in the third and fourth PCA dimensions on both the Group SAE and normal SAE (this is similar to the result from our circle paper). There were a few differences between the Group and normal SAEs:
Other Things We Tried
We also tried gated and topk Group SAEs. For these we did not see the same improvement in variance explained at the same sparsity (topk especially seemed to work badly), and we did not investigate these much further.
Experimenting with learned groups
Motivation and Ideas
The naive way of choosing group sizes is to fix them beforehand. Once you do so, the L1 of L2 penalty with fixed group sizes effectively incentivizes the model to group decoder vectors that fire together a lot (in other words, group the ones that have a high jaccard similarity). However, there are problems with this approach:
We came up with some ideas to fix these problems, some of which we tried and some of which we did not:
Learned Group Space
I was particularly interested in idea 4, “group space.” Before moving to SAEs, I tried experiments training on simple synthetic data to see what "forces" worked to learn groups successfully. For this simple task, I trained a simple embedding table E. The embedding table is trained on sets T⊂S that should be part of the same group. The loss of the model is then
L=positive_distance_loss(E(T),E(T))−negative_distance_loss(E(T),E(S−T))
Here "positive_distance_loss" is some loss that increases as points get farther apart, and "- negative_distance_loss" is some loss that decreases as points get farther apart. The idea is that the model should learn to position groups in space from seeing the co-occurence. I tried setting both positive and negative loss functions to be thresholded distance functions with different thresholds (0.1 and 1), so that groups should be within distance 0.1 and non groups should be at least distance 1 away. The experiments here are with embedding dimension 2 (higher dimensions did not seem to help).
When the task is easy and there is no co-occurence between groups, this works well! For this setting, the model gets only (0, 1) OR (2, 3) OR (3, 4) OR (5, 6) etc. Here are the embeddings over time for |S| = 100.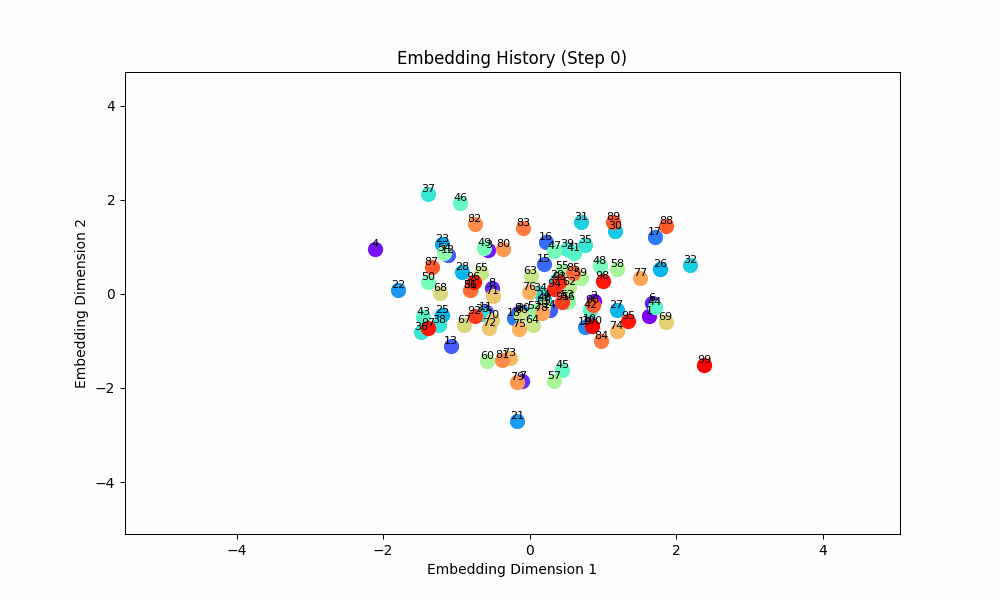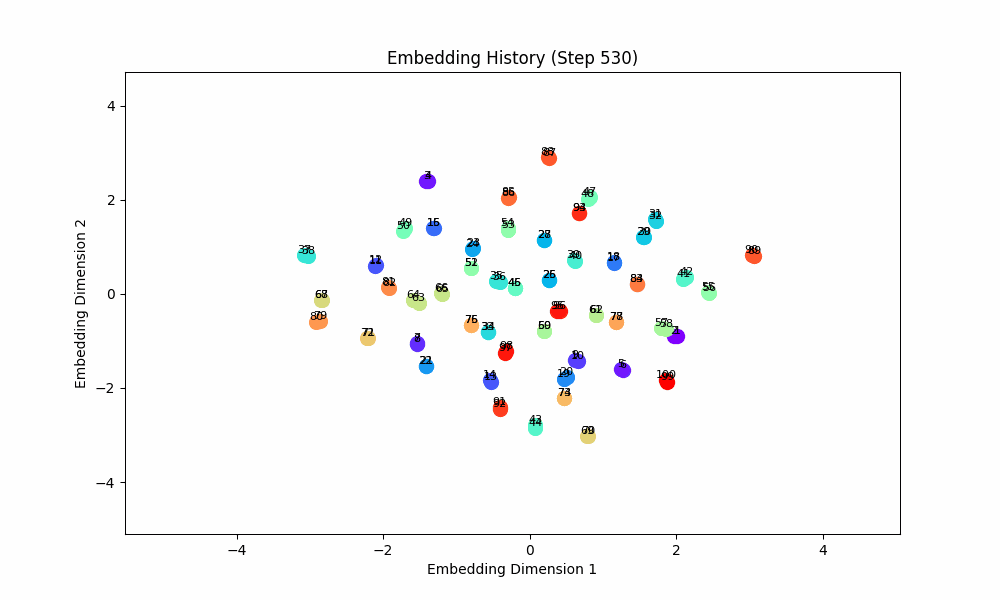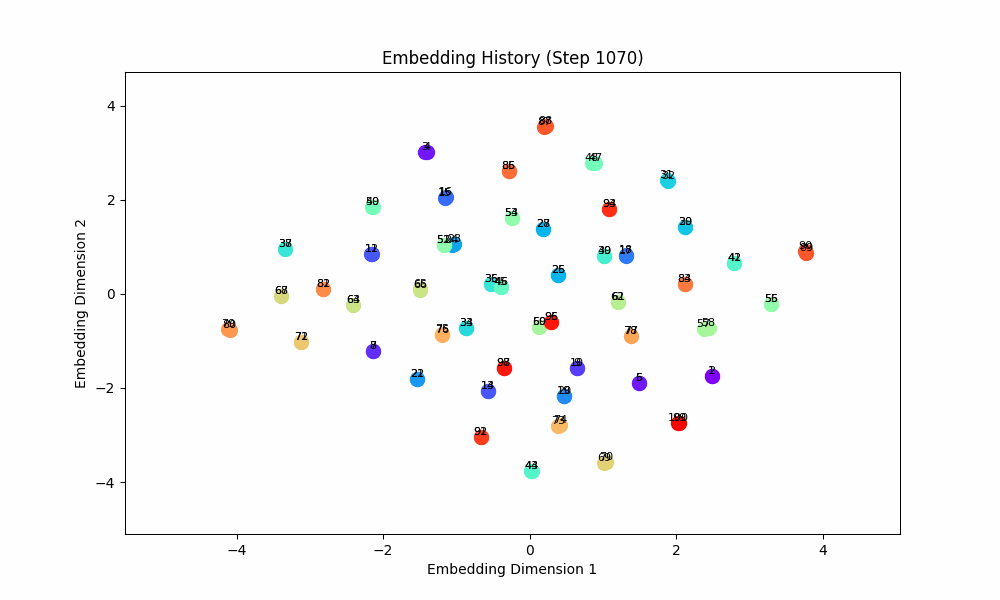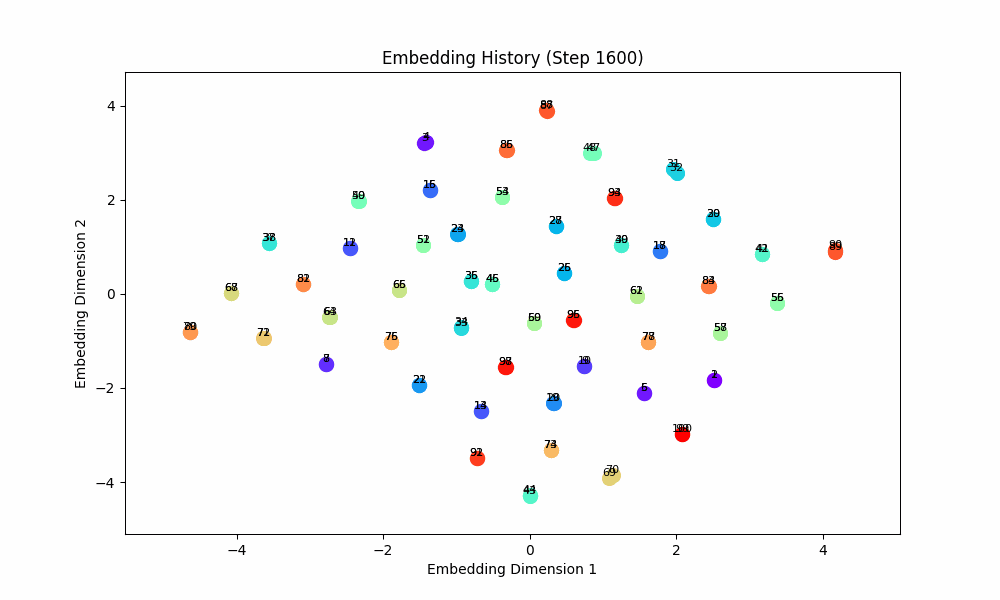
However, when the groups co-occur with some probability, the setup doesn't quite work, although the results are at least visually interesting! For this setting, I had all pairs of (0, 1), (2, 3), (4, 5), ... occur independently with probability 0.1. The true groups are still learned, but the points as a whole wrap around in a circular shape because the infrequent incentive to stay close from groups randomly occuring together are a force pushing them together. These gifs are from slightly different loss functions (I think on one I did the inverse square of the distance instead of the raw distance).
Conclusion
These results aren't exactly "negative" in that they fail at some task, but rather "negative" in that they don't seem to accomplish anything useful. This is another reason that I'm somewhat skeptical of directions like this: we spent 3 months working on an interesting "nerd-snipy" direction, but didn't really end up with anything satisfying.