Here’s a conceptual problem David and I have been lightly tossing around the past couple days.
“A is a subset of B” we might visualize like this:
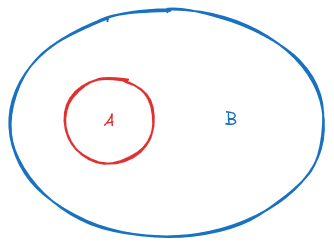
If we want a fuzzy/probabilistic version of the same diagram, we might draw something like this:
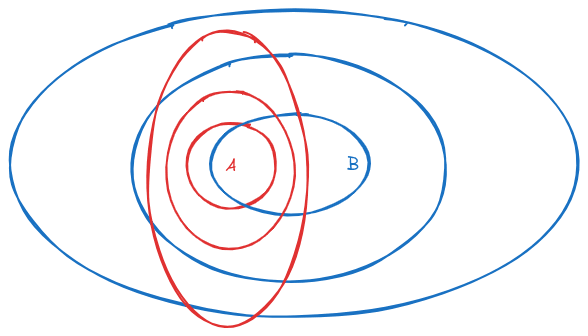
And we can easily come up with some ad-hoc operationalization of that “fuzzy subset” visual. But we’d like a principled operationalization.
Here’s one that I kinda like, based on maxent machinery.
Background Concept 1: Encodes The Same Information About As Itself
First, a background concept. Consider this maxent problem:
Or, more compactly
In English: what is the maximum entropy distribution for which (the average number of bits used to encode a sample from using a code optimized for distribution ) is at most (the average number of bits used to encode a sample from using a code optimized for )?
The solution to this problem is just .
Proof
First, the constraint must bind, except in the trivial case where is uniform. If the constraint did not bind, the solution would be the uniform distribution . In that case, the constraint would say
(because the uniform distribution has maximal entropy)
… but then adding yields , which can be satisfied iff the two distributions are equal. So unless is uniform, we have a contradiction, therefore the constraint must bind.
Since the constraint binds, the usual first-order condition for a maxent problem tells us that the solution has the form , where is a normalizer and the scalar is chosen to satisfy the constraint. We can trivially satisfy the constraint by choosing , in which case normalizes the distribution and we get . Uniqueness of maxent distributions then finishes the proof.
So conceptually, leveraging the zen of maxent distributions, the constraint encodes the same information about as the distribution itself.
Background Concept 2: … So Let’s Use Maxent To Fuse Distributions?
Conceptually, if the constraint encodes all the information from into a maxent problem, and the constraint encodes all the information from into a maxent problem, then solving the maxent problem with both of those constraints integrates “all the information from both and ” in some sense.
Qualitatively, here’s what that looks like in an example:
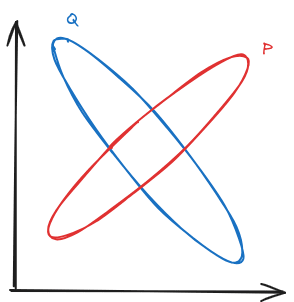
says that is probably in the red oval. says that is probably in the blue oval. So together, they conceptually say that is probably somewhere in the middle, roughly where the two intersect.
Mathematically, the first order maxent condition says , for some (which we will assume are both positive, because I don’t want to dive into the details of that right now). For any specific value, and can be no larger than 1, but they can be arbitrarily close to 0 (they could even be 0 exactly). And since they’re multiplied, when either one is very close to 0, we intuitively expect the product to be very close to 0. Most of the probability mass will therefore end up in places where neither distribution is very close to 0 - i.e. the spot where the ovals roughly intersect, as we’d intuitively hoped.
Notably, in the case where and are uniform over their ovals (so they basically just represent sets), the resulting distribution is exactly the uniform distribution over the intersection of the two sets. So conceptually, says something like “ is in set ”, says something like “ is in set ”, and then throwing both of those into a maxent problem says something like “ is in and is in , i.e. is in the intersection”.
So that hopefully gives a little intuition for how and why maxent can be used to combine the information “assumed in” two different distributions .
Something Like A Subset Relation?
What if we throw and into a maxent problem, but it turns out that the constraint is nonbinding? Conceptually, that would mean that already tells us everything about which tells us (and possibly more). Or, in hand wavy set terms, it would say that is a subset of , and therefore puts a strictly stronger bound on .
In principle, we can check whether ’s constraint is binding without actually running the maxent problem. We know that if ’s constraint doesn’t bind, the maxent solution is , so we can just evaluate ’s constraint at and see if it’s satisfied. The key condition is therefore:
’s constraint is nonbinding iff that condition holds, so we can view as saying something conceptually like “The information about implicitly encoded in is implied by the information about implicitly encoded in ” or, in the uniform case, “ is a subset of ”.
Now for an interesting check. If we’re going to think of this formula as analogous to a subset relationship, then we’d like to have transitivity: and implies . So, do we have
( and ) implies
?
Based on David’s quick computational check the answer is “no”, which makes this look a lot less promising, though I’m not yet fully convinced.