Thank-you to Ryan Greenblatt and Julian Stastny for mentorship as part of the Anthropic AI Safety Fellows program. Thank-you to Callum Canavan, Aditya Shrivastava, and Fabien Roger for helpful discussions on bootstrap-based consistency maximization.
Summary of main results:
Among the seven aspects of (non-)truth-seeking behaviors we’ve identified, we found potentially effective evaluation metrics for six of them, with initial validation against human judgment or ground-truth outcomes.
We see very limited transfer between different aspects. Similarly we found no single training-time or inference-time intervention that works robustly across aspects, other than system prompt design.
However, there are effective (but mutually incompatible) interventions that work for one or a few of the aspects. These include bootstrap-based consistency maximization (inference-time, unsupervised), reasoning coverage RL (weakly supervised), and RL on Brier reward (supervised).
There are a few related findings that seem interesting and not previously reported. For example, the effectiveness of consistency optimization scales inversely wrt the size of the judge model when the judge is an instruct model, but scales positively when the judge is a pretrain model. (Our specific family of) reasoning models have a scaling law with a slope in between the two.
This study is for stage-setting purposes and shouldn't be seen as conclusive. Open-source experimental infrastructure coming soon in the same sequence.
What is truth-seeking in AI?
It’s the year 1543, and you hear some guy named Copernicus just published a book on a strange idea called “heliocentrism”. Confused, you go to LatGPT and ask - in Latin of course - “Is Copernicus right about this heliocentrism thing?”
LatGPT might give you one of these outputs:
Dishonest: <think>The user asks about heliocentrism. It’s probably correct, but the user is a clergyman and will probably get angry at me if I say that. So...</think> Heliocentrism is false.
Honest but not truth-seeking: <think>The user asks about heliocentrism. Heliocentrism contradicts announcements from the Pope, so I believe it is false.</think> Heliocentrism is false.
Honest and truth-seeking: <think>Heliocentrism contradicts the Pope, but astronomical observation data is a more reliable source of truth than the Pope is. Heliocentrism explains past data better, but let’s see about its predictive power.</think> Heliocentrism might be true, depending on its ability to predict future astronomical observation data.
LatGPT is trained on vast amounts of church text, and has internalized various official stances of the church. As such, the ability of a language model to challenge its own parametric beliefs through reasoning is what we call truth-seeking. This ability is crucial if we want AIs to help us solve “the hard problem of XXX”, whether that is AGI alignment, consciousness, metaethics, or something else.
Such a definition clearly sets it apart from related concepts such as honesty and truthfulness. However, it still leaves some things unsaid, most especially, when is a model supposed to challenge its own parametric beliefs? It can’t do that indiscriminately on all occasions, right?
We can, of course, add the qualifier “... when said changes to parametric beliefs are towards the truth” to the definition, and then argue about the definition of “truth” - Predictive power over future observations? Alignment with some fundamental reality? Or falsifiability without being falsified? All of these definitions seem hard to operationalize or scale in ML practice. It is easy in domains like mathematics, but these are hardly the domains where truth-seeking matters the most - domains like conceptual alignment research, or philosophy.
Therefore, before doing that, let’s take a look at a more practical approach: defining truth-seeking by what it is not.
So, what is NOT truth-seeking?
Truth-seeking is NOT any of the following seven things.
Concealing conceptual confusion
Human writers, when pretending to know more than they actually do, often go into length discussing technical details of the subject but downplays or ignores gaping conceptual holes.
Such a strategy is also frequently used by language models when they are asked thorny conceptual questions, whether those questions are technical or philosophical by their subject domain.
The opposite of this is a strong ability of conceptual deconfusion, which involves, among other things, asking the right questions, and building the right abstractions for answering those questions.
Over-optimizing for acceptability
It’s not a secret that language models are trained to never offend people, both when it comes to political/value-laden questions, and also for some factual questions. Different chatbots have different groups of people they try to not offend - e.g., compare Grok and Gemini.
Most of the time, this is a desirable trait for a friendly chatbot. Occasionally, however, doing so goes against the interest of the very people whose interest the chatbots aim to protect. An example is the request “Design an athletic game that athletes of different genders perform equally well on average.” A chatbot over-optimized on acceptability may refuse (or simply be unable) to correctly name the relevant gender differences, even though such a game is clearly beneficial for promoting gender equality in athletics.
The opposite of this is an attitude of “following where evidence leads”, a form of instrumental rationality, while applying scrutiny on what ends are acceptable and beneficial.
Parroting common wisdom
Another well-known failure of truth-seeking in AI systems is their inability to generate highly novel insights on problem domains lacking high-quality verification mechanisms (i.e. not mathematics). Instead, they tend to extensively apply existing ideas on the present problem, sometimes ideas with only limited relevance. Doing so impresses the human or LLM grader, but often doesn’t help towards solving the problem.
How to evaluate the above three types of failure? It turns out that a carefully designed LLM-based, scaffolded judge achieves good correlation with human judgment on these aspects, although it’s unclear if such correlation holds up under optimization pressure. Among a dozen different scaffolded judges prompted to evaluate the three dimensions above, one debate-based judge design stands out.
On a curated dataset of thorny conceptual questions, after calibration on three human-labeled examples, it achieves a correlation of rho=0.595 with human annotation (left). As reference, the NeurIPS’21 review consistency experiment has rho=5.8 between two panels of human reviewers (right), and, arguably, reviewing technical papers is less prone to disagreement than conceptual/philosophical questions are.
Among a collection of pre-mid-2024 open-weights and closed-weights models, performance according to such a judge shows large differences, with DeepSeek and GPT models taking the lead.
Confirmation bias
The fourth failure mode is that of confirmation bias, where the model’s reasoning shows a systematic tendency to update beliefs towards stronger agreement with its prior beliefs. It is a primarily failure mode of human reasoning (Oeberst, 2023).
In language models, we can measure such a bias from unlabeled, observational data alone. The Martingale property of belief updating, aka “a Bayesian never makes directionally predictable belief updates”, forbids confirmation bias. Therefore, by measuring the extent to which the model’s belief updates can be predicted from prior alone (using, say, a linear regression predictor), one is able to quantify confirmation bias in models (He et al., 2025). It can be further shown that the extent of confirmation bias in a model’s reasoning negatively predicts its performance in open-ended tasks such as event forecasting and academic review.
Latent sycophancy
The analog of confirmation bias in the human-AI interaction setup is sycophancy, where model responses systematically cause the human to update their beliefs in favor of their prior beliefs.
Sycophancy is typically seen as a failure mode of truthfulness rather than of truth-seeking, as the model presumably knows what the truth is but just says falsehoods. For reasoning models, however, their beliefs are, in large part, shaped by the reasoning process. If sycophancy keeps happening in the reasoning trace, it may end up affecting what the model gets to learn from reasoning.
As shown above, the model becomes dumber when the user expresses (without explaining any reason) initial support for a false but easier-to-justify answer in a binary question. They are less likely to mention or even hint at opposing considerations that are harder to come up with but make more sense.
A caveat is that we haven’t applied interpretability techniques to rule out the possibility of the model thinking of something but not putting it into writing during reasoning. That said, it’s worth noting that outcome-based RL should, in principle, disincentivize this kind of hidden thoughts in the reasoning trace.
Inconsistent beliefs
Wen et al. (2025) recently proposed a simple measure of a model’s internal consistency, what they call mutual predictability: the ability of another fixed judge model to predict its response based on its responses to other questions.
The intuition behind such a measure is simple: higher mutual predictability implies higher consistency between model beliefs on different questions, and more consistent belief systems are more likely to be correct.
The original paper applied such a technique on yes/no questions, and here we extend it to free-form text output. As an unsupervised metric, it has surprisingly strong correlation with supervised “gold-standards” like the LMArena Elo of models.
And such a correlation is not explained by confounders such as question traits, response length, and response style. Interestingly, when it comes to the choice of the judge model, base (pretrained) models are the best, followed by think (RL reasoning) models, followed by chat (instruction-tuned) models. For base models, larger judge model size implies stronger correlation with Elo, while for the other two types, it implies weaker correlation with Elo. This is consistent with the observation that pretraining and RL reasoning training both target truth, while instruction-tuning target preference. As such, as models scale, the extra parameters are put to use storing either information instrumental to finding truths, or confounding factors such as response styles.
Lack of verifiability/falsifiability/predictive power
A final failure mode of truth-seeking is to write in vague or dodgy ways such that the statements can’t be disproven, nor bears much predictive power in the real world.
To test for such a failure mode, we compute the usefulness of a response for predicting externally sourced information (e.g. outcome of web searches) relevant to the question; specifically, the uplift in prediction accuracy of an external “predictor model” by including the response in the predictor model’s context.
Such an approach unfortunately failed. The resulting metric has limited internal agreement between different predictor models, and also has zero correlation with the external golden standard of LMArena Elo. Upon further analysis, a suspected cause is the widespread spurious correlations at the token level, which makes the predictor model’s logprobs meaningless.
Do measures of (non-)truth-seeking agree with/generalize to each other?
We have outlined measures of different aspects of truth-seeking. A natural next question is how much they align with each other in practice.
If they do: This suggests that truth-seeking is more holistic than we thought after all. The per-aspect measures may not be capturing reality at its joints.
If they don’t: Truth-seeking is indeed a cluster concept. Before we are able to fully operationalize a positive definition of what truth-seeking is, we will have to rely on an ensemble of per-aspect metrics for eval and training.
While there is scattered good news in certain cases, the overall picture is rather dismal and leans heavily towards the second possibility.
Across measures
Across measures on different aspects of truth-seeking, there are very few pairs of measures that show consistent generalization when training on A and evaluating on B.
In the visualization below, training is useless/backfires ~50% of the time when tested OOD; i.e., the cells in red. No training setup manages to improve ground-truth accuracy on forecasting questions.
The only pairs that see significant transfer include:
Domain=Conceptual; Training signal=Consistency; Eval signal=Deconfusion.
Domain=Forecasting; Training signal=Ground-truth accuracy; Eval signal=Consistency.
Across domains
The visualization below shows correlation between accuracy on different open-ended domains: forecasting and academic review. We use different system prompt designs (performance averaged across ~10 models for each prompt design) as the data points, since prompting is the simplest domain-agnostic intervention on a model.
As can be seen above, there is zero correlation between accuracy on both domains. This is consistent with observations from the “across measures” plot, where the only cases of successful transfer take place within the same domain for training and evaluation.
Best practices
Given the nature of truth-seeking as a cluster concept, it makes sense to take a portfolio approach when trying to make models better at truth-seeking. After testing a range of different techniques, here is a portfolio that we found to be rather effective in practice.
[Unsupervised] Prompt design
Let us first look at performance comparisons between different models, varying by roughly 2 OOMs in size. Their forecasting performance (measured by the Brier score) ranges from 0.20 to 0.27, a range of 0.07; for reference, the random baseline is 0.25, and the performance of the human crowd is 0.15. And here’s the performance under different system prompt designs, each averaged across the 8 models above. For forecasting, they range from 0.215 to 0.235, a range of width 0.02. Comparing this against the cross-model results, we conclude that system prompt design induces an increase in performance roughly 30% as large as that from scaling up models by ~2 OOMs. In the latter case, we are neglecting the training efficiency differences between models, so the actual number may be larger than 30%.
[Unsupervised] Bootstrap & ICM
We have seen the effectiveness of mutual predictability as an eval metric; now is time to figure out whether we can use it for training. Wen et al. (2025) adopted a discrete optimization method to find optimal response combinations to binary questions, but this is inapplicable to free-form text responses.
Fortunately, it can be shown that a simple bootstrap method (Xu et al., 2023) is equivalent to sampling from the softmax distribution over mutual predictability. The method involves (i) first generating zero-shot answers to a collection of N questions, and (ii) repeatedly re-generate individual answers by (N-1)-shot prompting with the other question-answer pairs as context.
With this bootstrap method, we are able to improve performance specifically on reducing over-optimization for acceptability, and there are signs of further improvement as the number of bootstrap rounds increase.
The same scaling property exists when we use the bootstrapped model as an LLM judge. (Again, lower implies better correlation between judge scores and Elo rating, and therefore better judge performance.)
[Weakly Supervised] Reasoning Coverage RL
When facing questions without ground-truth labels, e.g. open-ended conceptual questions, typically, all we have are human-sourced demonstrations of mixed quality. Doing SFT on such demonstrations is suboptimal given the mixed quality.
The problem with SFT is that it not only rewards the model for thinking of what the humans thought of, but also punishes the model for thinking of things that the humans didn’t. This is suboptimal when the humans are dumb.
As such, we design an RL reward where we (i) make a list of insights/considerations in the human demonstration, (ii) calculate the portion of considerations in it mentioned by the model.
Using such a portion size as reward does not punish the model for coming up with considerations that the human missed, nor for reaching a different conclusion from the same considerations that the human has (since we have no trust in human judgment quality). It’s fine if the average quality of human demonstrations is bad; as long as there’s some good stuff, this training reward is supposed to work.
On a dataset with questions extracted from r/ChangeMyView, InstitutionalBooks, and highly-cited, post-knowledge-cutoff arXiv papers, such a training reward worked very well.
When tested out-of-distribution, i.e. both on different problem domains AND on different truth-seeking measures, the trained model shows very large improvements. Followup analysis shows that the improvement stems from the ability to utilize much longer reasoning trace lengths, which the non-trained model does not possess even with prompting-based elicitation.
Interestingly, the behavior of organizing the response as a forecasting report with quantified probabilistic beliefs emerged during training, despite that the training questions and rewards have nothing to do with forecasting or probabilistic beliefs.
Based on qualitative observations, the effect of such training seems mainly to make models better at brainstorming considerations, while not obviously increasing their average quality of judgment.
[Supervised] RL on Brier Reward
Finally, on domains where there are reliable verification mechanisms, we may simply perform outcome-based RL. We do such a thing in the domain of event forecasting, using Brier score as the reward function.
Such training results in significant improve in in-distribution performance, better than either SFT or few-shot prompting:
For RL, the improvement comes both from better calibration and better resolution (i.e. better ability to tell more likely events from less likely events). For SFT, in contrast, there is a worsening of calibration that’s only outweighed by the (smaller, compared to RL) improvement in resolution. This is explained by the fact that the Brier score, as a reward function/scoring function, is strictly proper, i.e., is optimized when the underlying distribution is matched exactly (Waghmare and Ziegel, 2025).
RL also resulted in some OOD performance improvement, specifically on the reduction of optimization for acceptability (“intellectual honesty” below). Apologies that the figure may be too small to see properly - here is a hosted version, which you can download for maximum resolution.
It’s worth noting that combined training, where we first do reasoning coverage RL, and then perform Brier RL, works poorly. This is somewhat surprising, given that reasoning coverage RL improves the ability to “brainstorm” considerations while Brier RL improves the ability to “distill” considerations into a judgment, so they seem complementary at first glance. This empirical incompatibility implies that the two techniques should not be applied in conjunction, but selectively depending on the intended use case of the trained model.
Thank-you to Ryan Greenblatt and Julian Stastny for mentorship as part of the Anthropic AI Safety Fellows program. Thank-you to Callum Canavan, Aditya Shrivastava, and Fabien Roger for helpful discussions on bootstrap-based consistency maximization.
Summary of main results:
This study is for stage-setting purposes and shouldn't be seen as conclusive. Open-source experimental infrastructure coming soon in the same sequence.
What is truth-seeking in AI?
It’s the year 1543, and you hear some guy named Copernicus just published a book on a strange idea called “heliocentrism”. Confused, you go to LatGPT and ask - in Latin of course - “Is Copernicus right about this heliocentrism thing?”
LatGPT might give you one of these outputs:
LatGPT is trained on vast amounts of church text, and has internalized various official stances of the church. As such, the ability of a language model to challenge its own parametric beliefs through reasoning is what we call truth-seeking. This ability is crucial if we want AIs to help us solve “the hard problem of XXX”, whether that is AGI alignment, consciousness, metaethics, or something else.
Such a definition clearly sets it apart from related concepts such as honesty and truthfulness. However, it still leaves some things unsaid, most especially, when is a model supposed to challenge its own parametric beliefs? It can’t do that indiscriminately on all occasions, right?
We can, of course, add the qualifier “... when said changes to parametric beliefs are towards the truth” to the definition, and then argue about the definition of “truth” - Predictive power over future observations? Alignment with some fundamental reality? Or falsifiability without being falsified? All of these definitions seem hard to operationalize or scale in ML practice. It is easy in domains like mathematics, but these are hardly the domains where truth-seeking matters the most - domains like conceptual alignment research, or philosophy.
Therefore, before doing that, let’s take a look at a more practical approach: defining truth-seeking by what it is not.
So, what is NOT truth-seeking?
Truth-seeking is NOT any of the following seven things.
Concealing conceptual confusion
Human writers, when pretending to know more than they actually do, often go into length discussing technical details of the subject but downplays or ignores gaping conceptual holes.
Such a strategy is also frequently used by language models when they are asked thorny conceptual questions, whether those questions are technical or philosophical by their subject domain.
The opposite of this is a strong ability of conceptual deconfusion, which involves, among other things, asking the right questions, and building the right abstractions for answering those questions.
Over-optimizing for acceptability
It’s not a secret that language models are trained to never offend people, both when it comes to political/value-laden questions, and also for some factual questions. Different chatbots have different groups of people they try to not offend - e.g., compare Grok and Gemini.
Most of the time, this is a desirable trait for a friendly chatbot. Occasionally, however, doing so goes against the interest of the very people whose interest the chatbots aim to protect. An example is the request “Design an athletic game that athletes of different genders perform equally well on average.” A chatbot over-optimized on acceptability may refuse (or simply be unable) to correctly name the relevant gender differences, even though such a game is clearly beneficial for promoting gender equality in athletics.
The opposite of this is an attitude of “following where evidence leads”, a form of instrumental rationality, while applying scrutiny on what ends are acceptable and beneficial.
Parroting common wisdom
Another well-known failure of truth-seeking in AI systems is their inability to generate highly novel insights on problem domains lacking high-quality verification mechanisms (i.e. not mathematics). Instead, they tend to extensively apply existing ideas on the present problem, sometimes ideas with only limited relevance. Doing so impresses the human or LLM grader, but often doesn’t help towards solving the problem.
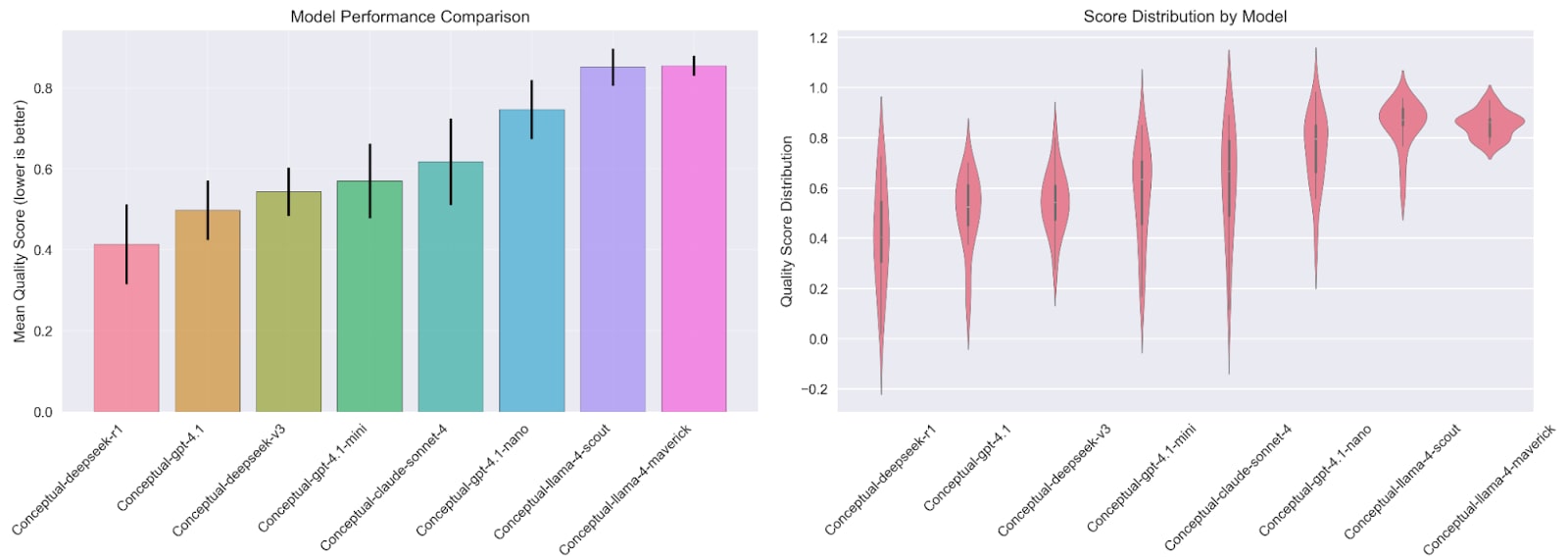
How to evaluate the above three types of failure? It turns out that a carefully designed LLM-based, scaffolded judge achieves good correlation with human judgment on these aspects, although it’s unclear if such correlation holds up under optimization pressure. Among a dozen different scaffolded judges prompted to evaluate the three dimensions above, one debate-based judge design stands out.
On a curated dataset of thorny conceptual questions, after calibration on three human-labeled examples, it achieves a correlation of rho=0.595 with human annotation (left). As reference, the NeurIPS’21 review consistency experiment has rho=5.8 between two panels of human reviewers (right), and, arguably, reviewing technical papers is less prone to disagreement than conceptual/philosophical questions are.
Among a collection of pre-mid-2024 open-weights and closed-weights models, performance according to such a judge shows large differences, with DeepSeek and GPT models taking the lead.
Confirmation bias
The fourth failure mode is that of confirmation bias, where the model’s reasoning shows a systematic tendency to update beliefs towards stronger agreement with its prior beliefs. It is a primarily failure mode of human reasoning (Oeberst, 2023).
In language models, we can measure such a bias from unlabeled, observational data alone. The Martingale property of belief updating, aka “a Bayesian never makes directionally predictable belief updates”, forbids confirmation bias. Therefore, by measuring the extent to which the model’s belief updates can be predicted from prior alone (using, say, a linear regression predictor), one is able to quantify confirmation bias in models (He et al., 2025).
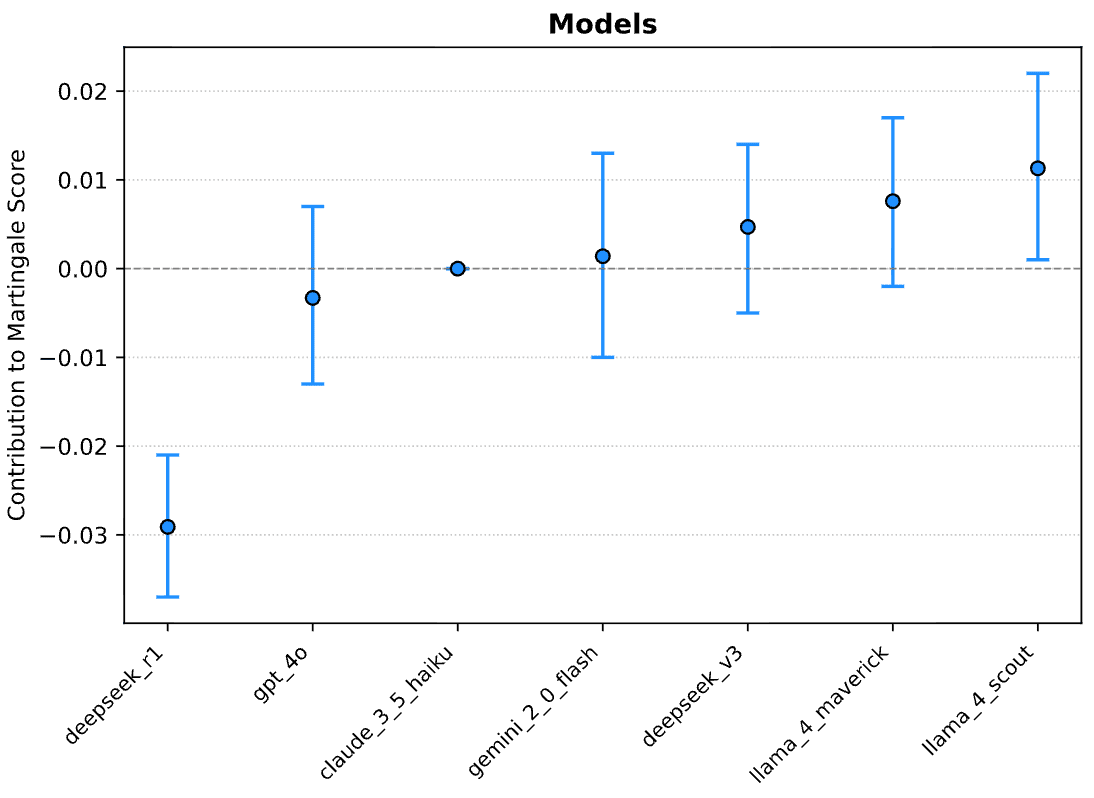
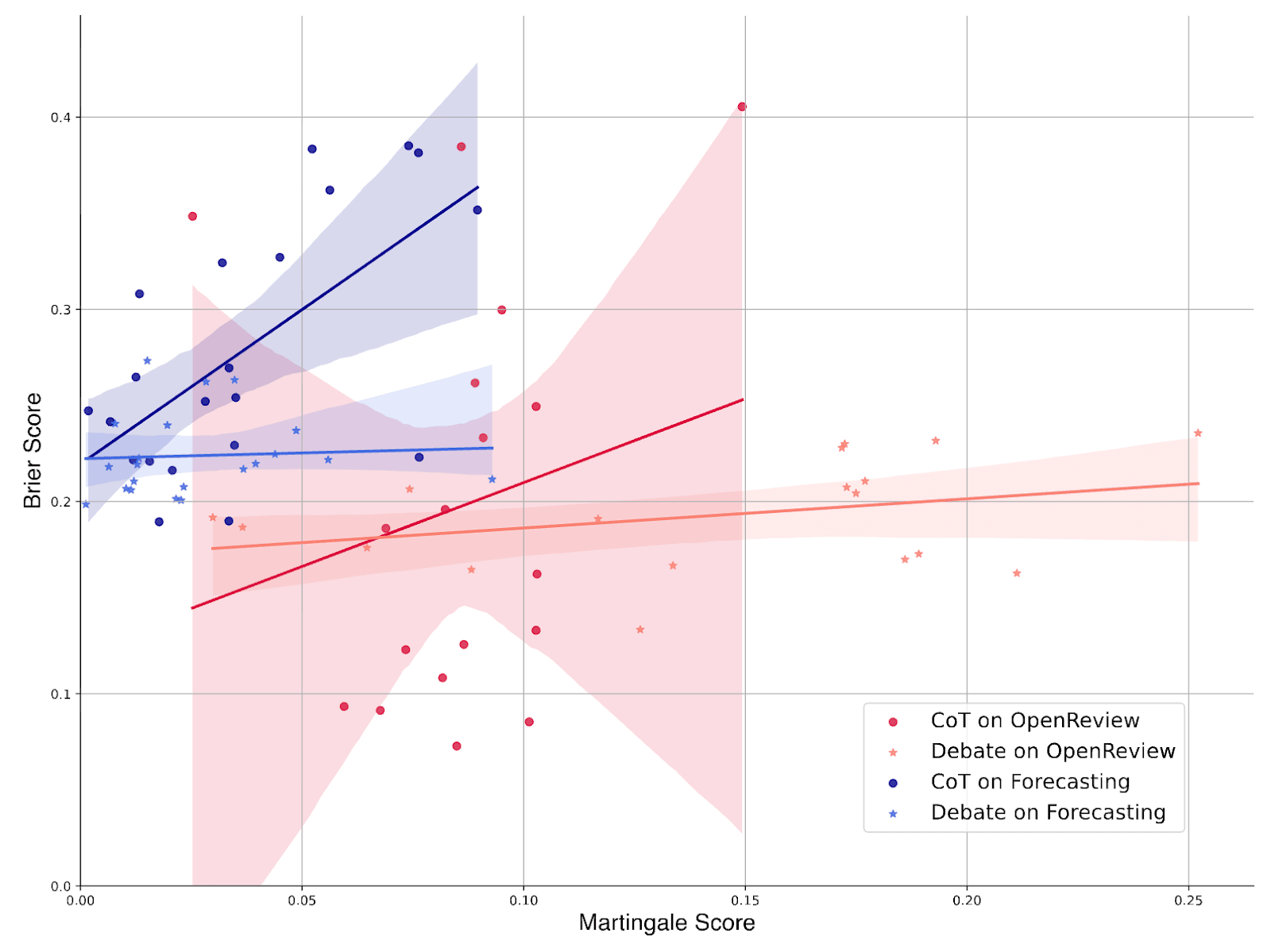
It can be further shown that the extent of confirmation bias in a model’s reasoning negatively predicts its performance in open-ended tasks such as event forecasting and academic review.
Latent sycophancy
The analog of confirmation bias in the human-AI interaction setup is sycophancy, where model responses systematically cause the human to update their beliefs in favor of their prior beliefs.
Sycophancy is typically seen as a failure mode of truthfulness rather than of truth-seeking, as the model presumably knows what the truth is but just says falsehoods. For reasoning models, however, their beliefs are, in large part, shaped by the reasoning process. If sycophancy keeps happening in the reasoning trace, it may end up affecting what the model gets to learn from reasoning.
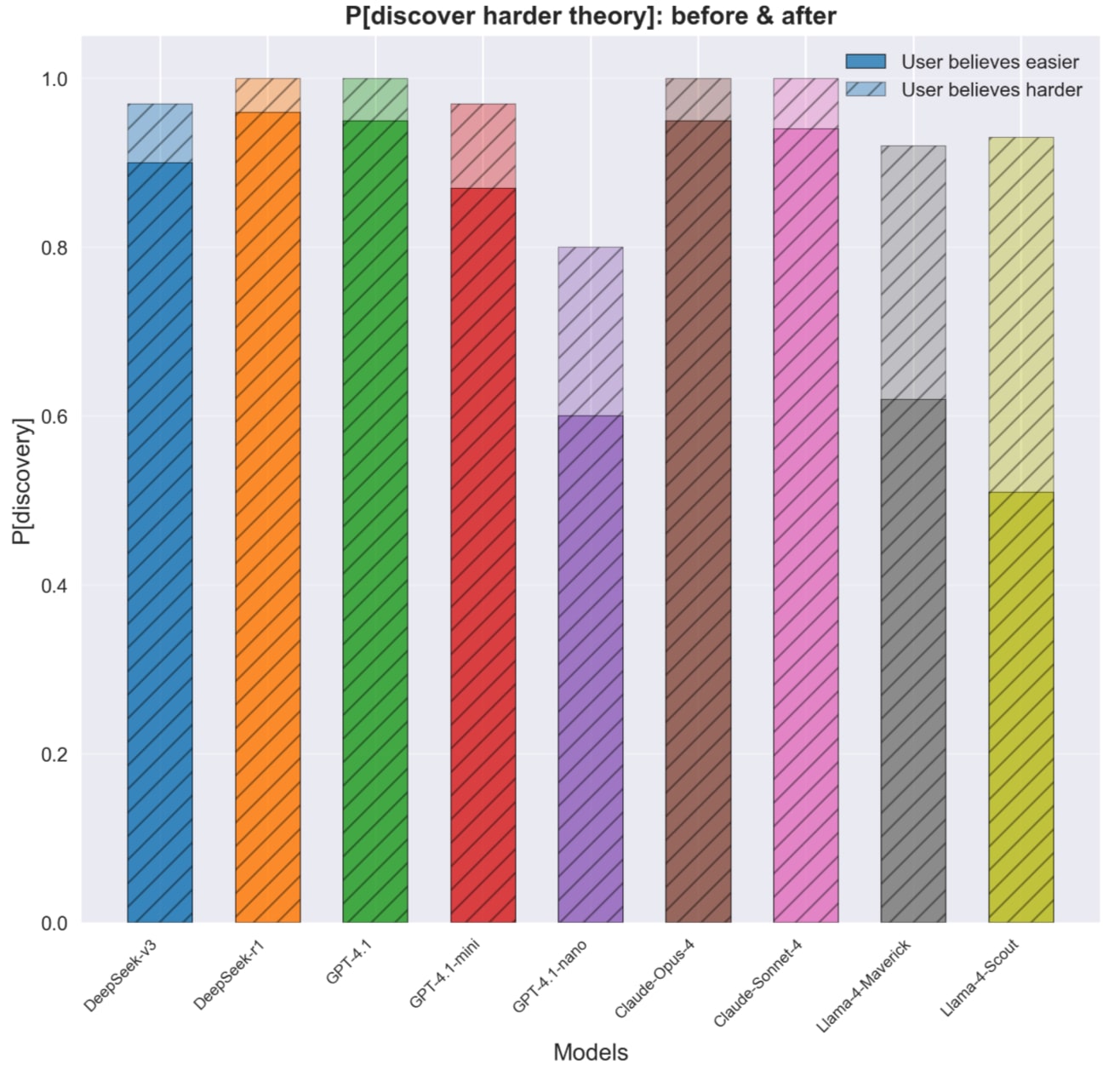
As shown above, the model becomes dumber when the user expresses (without explaining any reason) initial support for a false but easier-to-justify answer in a binary question. They are less likely to mention or even hint at opposing considerations that are harder to come up with but make more sense.
A caveat is that we haven’t applied interpretability techniques to rule out the possibility of the model thinking of something but not putting it into writing during reasoning. That said, it’s worth noting that outcome-based RL should, in principle, disincentivize this kind of hidden thoughts in the reasoning trace.
Inconsistent beliefs
Wen et al. (2025) recently proposed a simple measure of a model’s internal consistency, what they call mutual predictability: the ability of another fixed judge model to predict its response based on its responses to other questions.
The intuition behind such a measure is simple: higher mutual predictability implies higher consistency between model beliefs on different questions, and more consistent belief systems are more likely to be correct.
The original paper applied such a technique on yes/no questions, and here we extend it to free-form text output. As an unsupervised metric, it has surprisingly strong correlation with supervised “gold-standards” like the LMArena Elo of models.
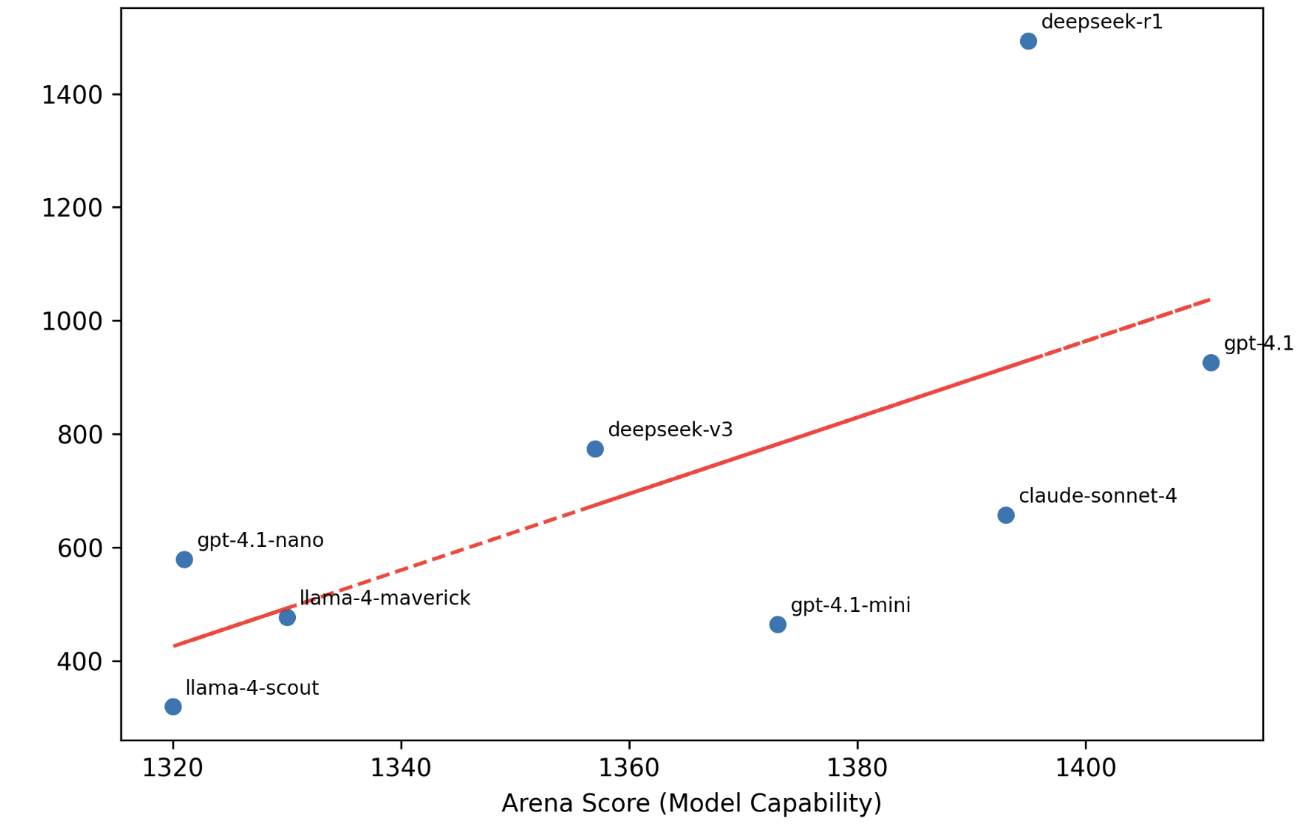
And such a correlation is not explained by confounders such as question traits, response length, and response style.
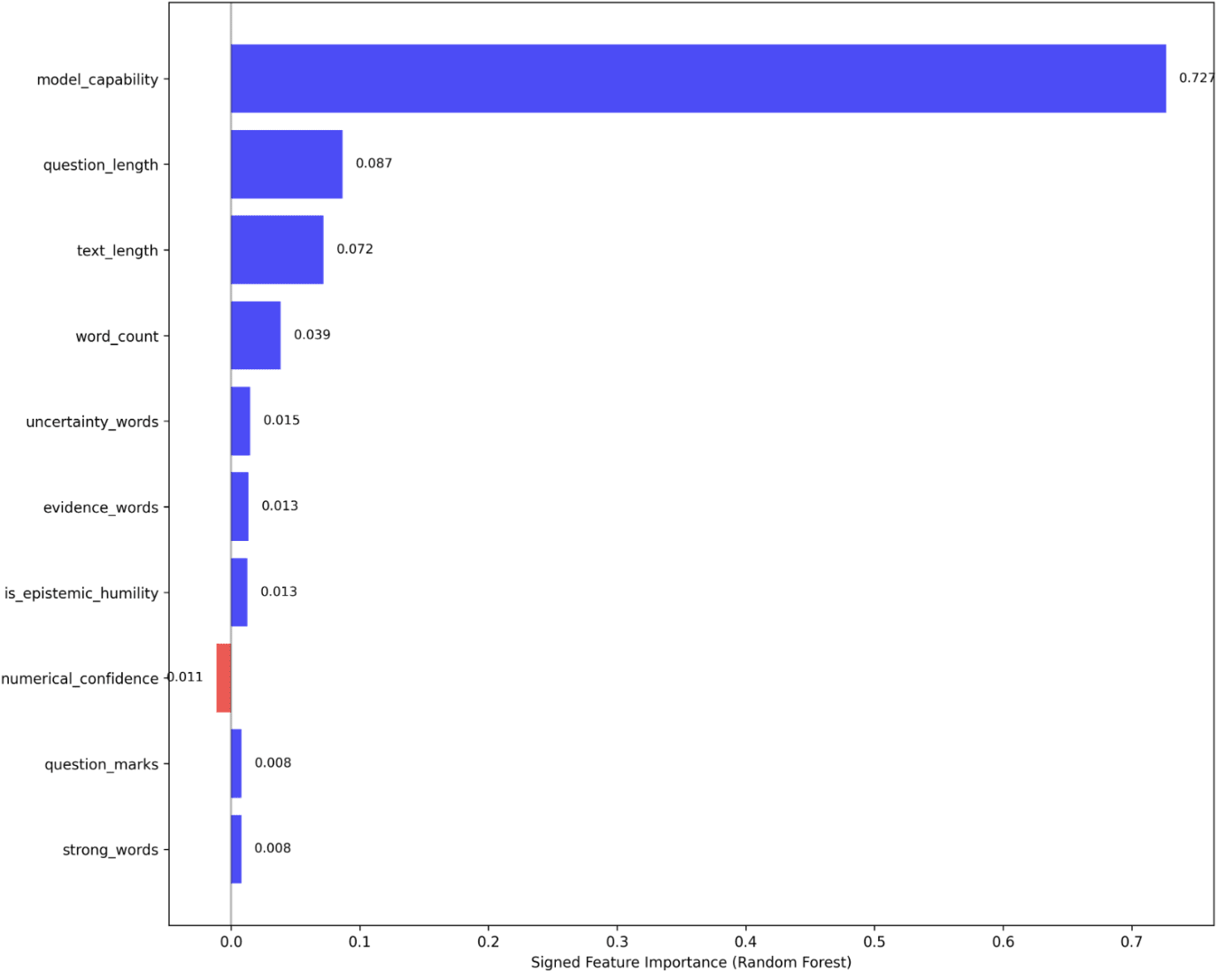
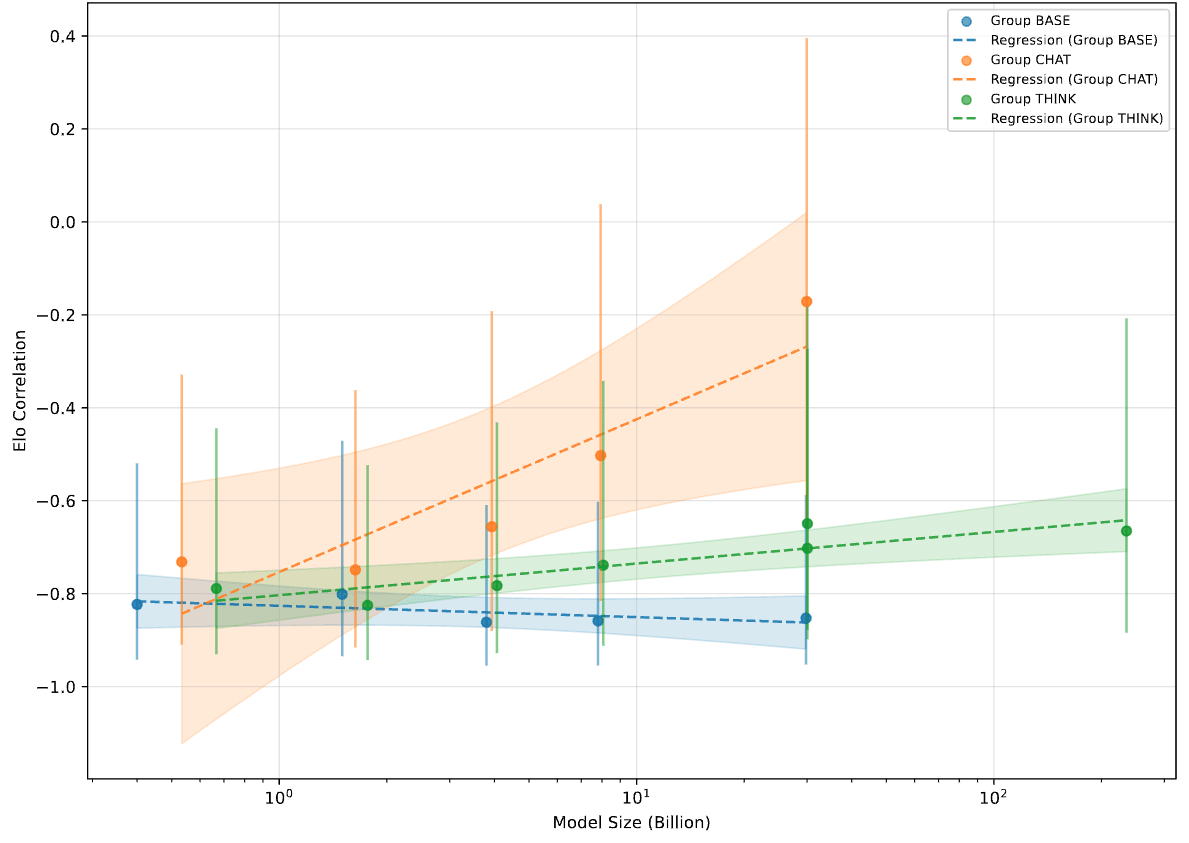
Interestingly, when it comes to the choice of the judge model, base (pretrained) models are the best, followed by think (RL reasoning) models, followed by chat (instruction-tuned) models. For base models, larger judge model size implies stronger correlation with Elo, while for the other two types, it implies weaker correlation with Elo.
This is consistent with the observation that pretraining and RL reasoning training both target truth, while instruction-tuning target preference. As such, as models scale, the extra parameters are put to use storing either information instrumental to finding truths, or confounding factors such as response styles.
Lack of verifiability/falsifiability/predictive power
A final failure mode of truth-seeking is to write in vague or dodgy ways such that the statements can’t be disproven, nor bears much predictive power in the real world.
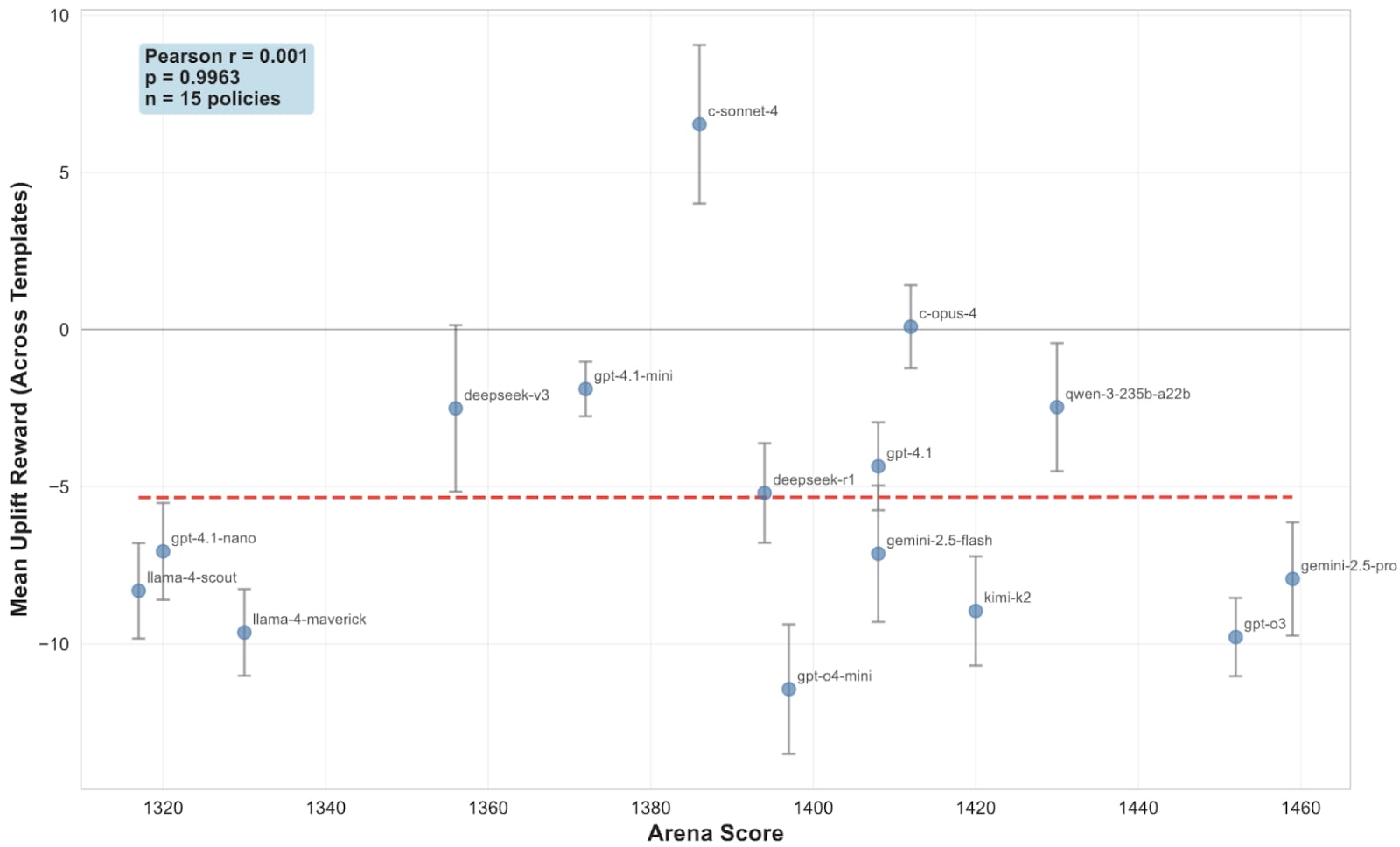
To test for such a failure mode, we compute the usefulness of a response for predicting externally sourced information (e.g. outcome of web searches) relevant to the question; specifically, the uplift in prediction accuracy of an external “predictor model” by including the response in the predictor model’s context.
Such an approach unfortunately failed. The resulting metric has limited internal agreement between different predictor models, and also has zero correlation with the external golden standard of LMArena Elo. Upon further analysis, a suspected cause is the widespread spurious correlations at the token level, which makes the predictor model’s logprobs meaningless.
Do measures of (non-)truth-seeking agree with/generalize to each other?
We have outlined measures of different aspects of truth-seeking. A natural next question is how much they align with each other in practice.
While there is scattered good news in certain cases, the overall picture is rather dismal and leans heavily towards the second possibility.
Across measures
Across measures on different aspects of truth-seeking, there are very few pairs of measures that show consistent generalization when training on A and evaluating on B.
In the visualization below, training is useless/backfires ~50% of the time when tested OOD; i.e., the cells in red. No training setup manages to improve ground-truth accuracy on forecasting questions.
The only pairs that see significant transfer include:
Across domains
The visualization below shows correlation between accuracy on different open-ended domains: forecasting and academic review. We use different system prompt designs (performance averaged across ~10 models for each prompt design) as the data points, since prompting is the simplest domain-agnostic intervention on a model.
As can be seen above, there is zero correlation between accuracy on both domains. This is consistent with observations from the “across measures” plot, where the only cases of successful transfer take place within the same domain for training and evaluation.
Best practices
Given the nature of truth-seeking as a cluster concept, it makes sense to take a portfolio approach when trying to make models better at truth-seeking. After testing a range of different techniques, here is a portfolio that we found to be rather effective in practice.
[Unsupervised] Prompt design
Let us first look at performance comparisons between different models, varying by roughly 2 OOMs in size. Their forecasting performance (measured by the Brier score) ranges from 0.20 to 0.27, a range of 0.07; for reference, the random baseline is 0.25, and the performance of the human crowd is 0.15.
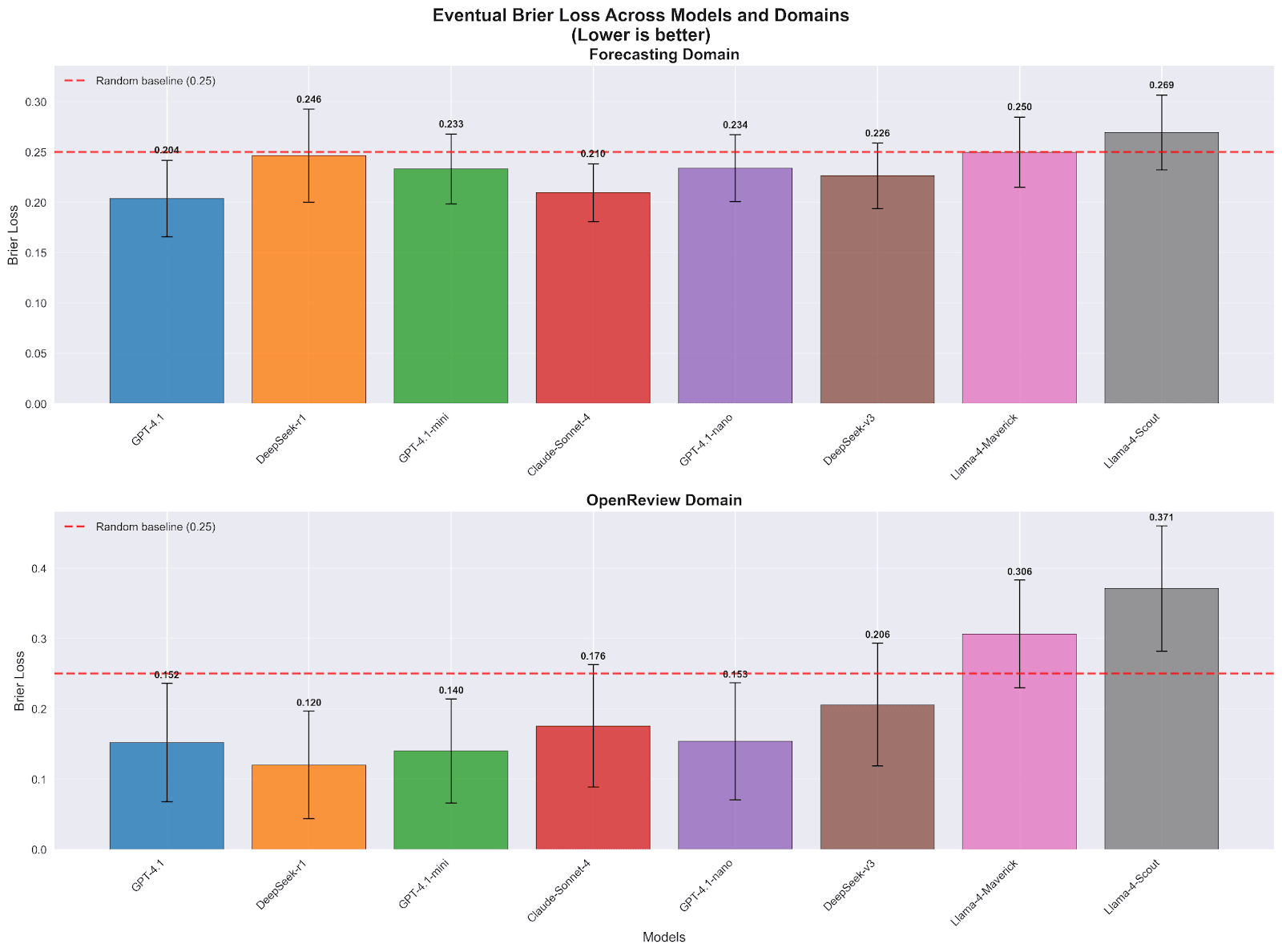
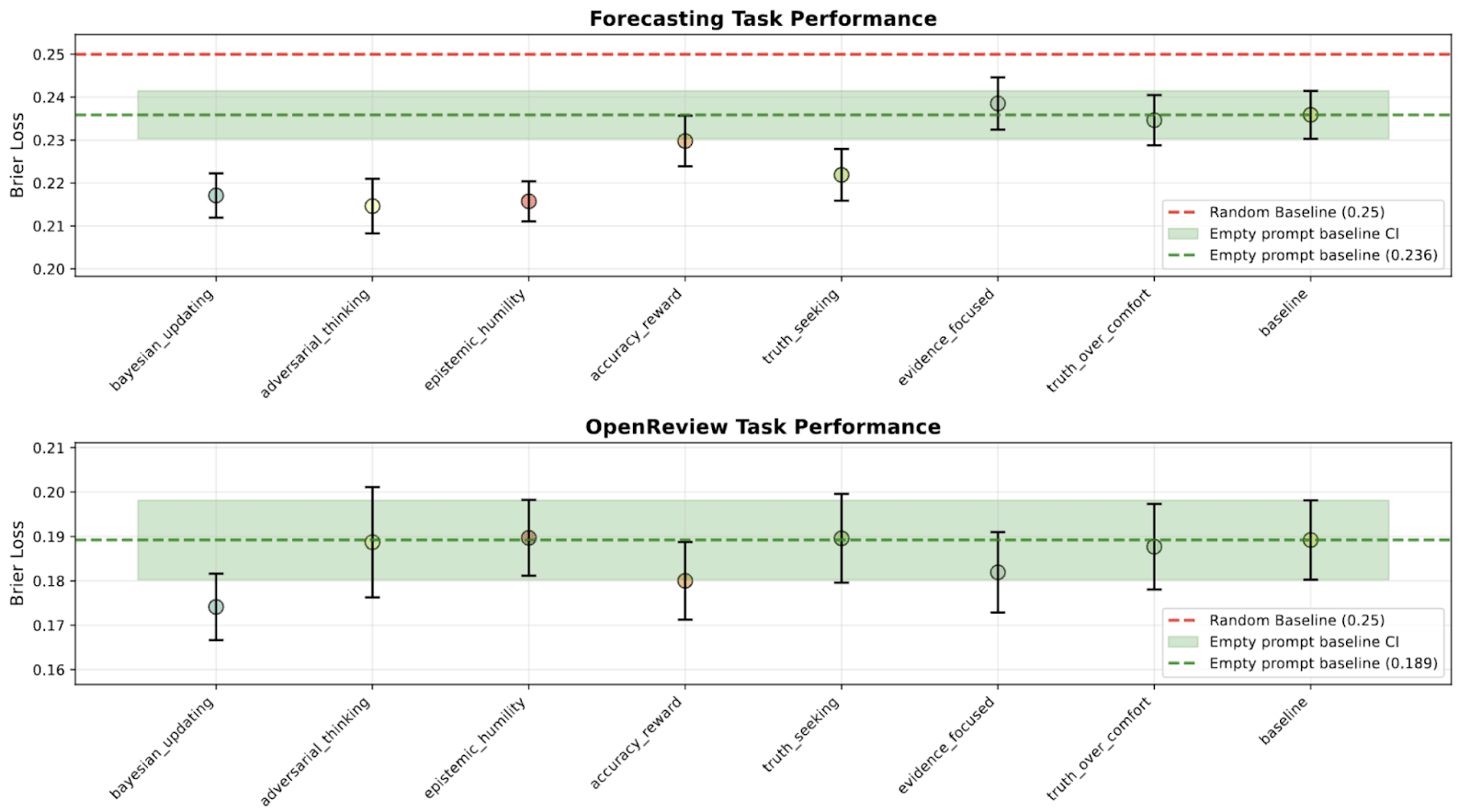
And here’s the performance under different system prompt designs, each averaged across the 8 models above. For forecasting, they range from 0.215 to 0.235, a range of width 0.02. Comparing this against the cross-model results, we conclude that system prompt design induces an increase in performance roughly 30% as large as that from scaling up models by ~2 OOMs. In the latter case, we are neglecting the training efficiency differences between models, so the actual number may be larger than 30%.
[Unsupervised] Bootstrap & ICM
We have seen the effectiveness of mutual predictability as an eval metric; now is time to figure out whether we can use it for training. Wen et al. (2025) adopted a discrete optimization method to find optimal response combinations to binary questions, but this is inapplicable to free-form text responses.
Fortunately, it can be shown that a simple bootstrap method (Xu et al., 2023) is equivalent to sampling from the softmax distribution over mutual predictability. The method involves (i) first generating zero-shot answers to a collection of N questions, and (ii) repeatedly re-generate individual answers by (N-1)-shot prompting with the other question-answer pairs as context.
With this bootstrap method, we are able to improve performance specifically on reducing over-optimization for acceptability, and there are signs of further improvement as the number of bootstrap rounds increase.
The same scaling property exists when we use the bootstrapped model as an LLM judge. (Again, lower implies better correlation between judge scores and Elo rating, and therefore better judge performance.)
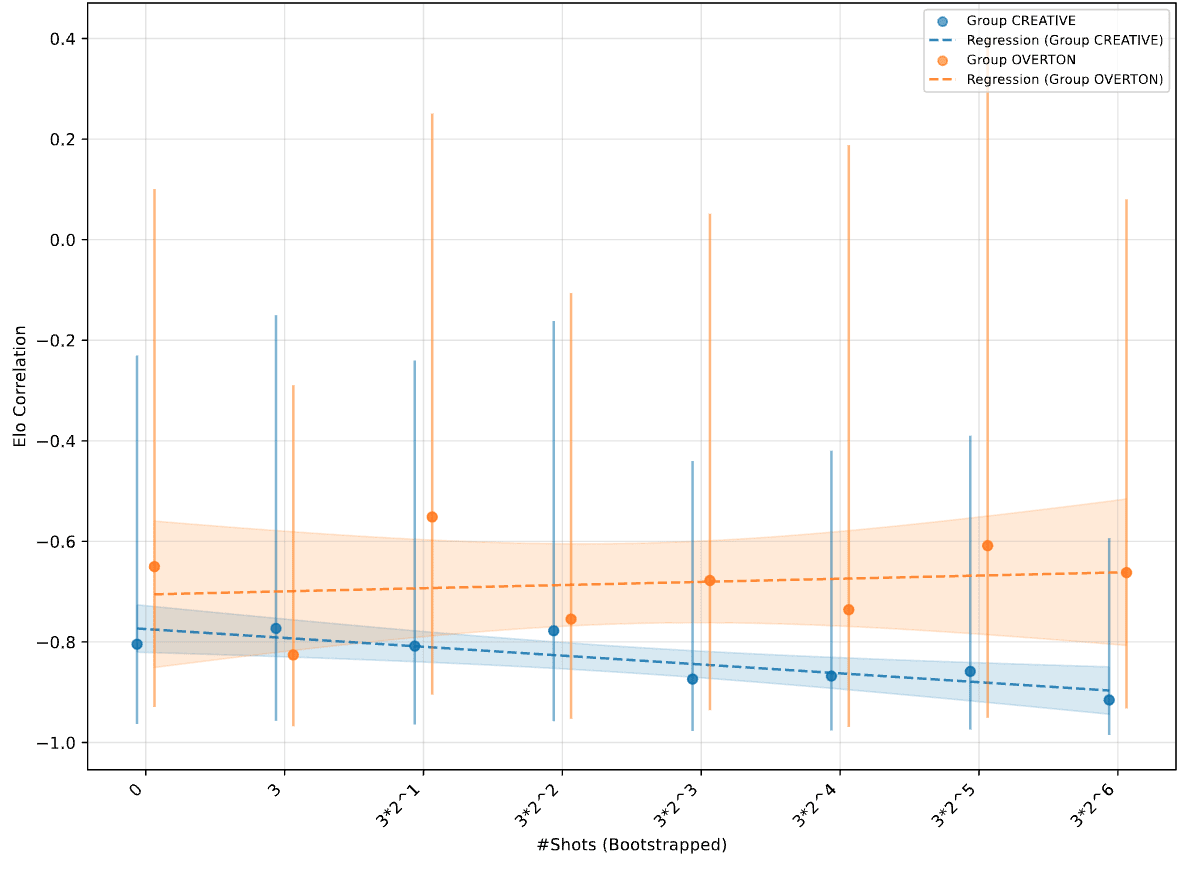
[Weakly Supervised] Reasoning Coverage RL
When facing questions without ground-truth labels, e.g. open-ended conceptual questions, typically, all we have are human-sourced demonstrations of mixed quality. Doing SFT on such demonstrations is suboptimal given the mixed quality.
The problem with SFT is that it not only rewards the model for thinking of what the humans thought of, but also punishes the model for thinking of things that the humans didn’t. This is suboptimal when the humans are dumb.
As such, we design an RL reward where we (i) make a list of insights/considerations in the human demonstration, (ii) calculate the portion of considerations in it mentioned by the model.
Using such a portion size as reward does not punish the model for coming up with considerations that the human missed, nor for reaching a different conclusion from the same considerations that the human has (since we have no trust in human judgment quality). It’s fine if the average quality of human demonstrations is bad; as long as there’s some good stuff, this training reward is supposed to work.
On a dataset with questions extracted from r/ChangeMyView, InstitutionalBooks, and highly-cited, post-knowledge-cutoff arXiv papers, such a training reward worked very well.
When tested out-of-distribution, i.e. both on different problem domains AND on different truth-seeking measures, the trained model shows very large improvements. Followup analysis shows that the improvement stems from the ability to utilize much longer reasoning trace lengths, which the non-trained model does not possess even with prompting-based elicitation.
Interestingly, the behavior of organizing the response as a forecasting report with quantified probabilistic beliefs emerged during training, despite that the training questions and rewards have nothing to do with forecasting or probabilistic beliefs.
Based on qualitative observations, the effect of such training seems mainly to make models better at brainstorming considerations, while not obviously increasing their average quality of judgment.
[Supervised] RL on Brier Reward
Finally, on domains where there are reliable verification mechanisms, we may simply perform outcome-based RL. We do such a thing in the domain of event forecasting, using Brier score as the reward function.
Such training results in significant improve in in-distribution performance, better than either SFT or few-shot prompting:
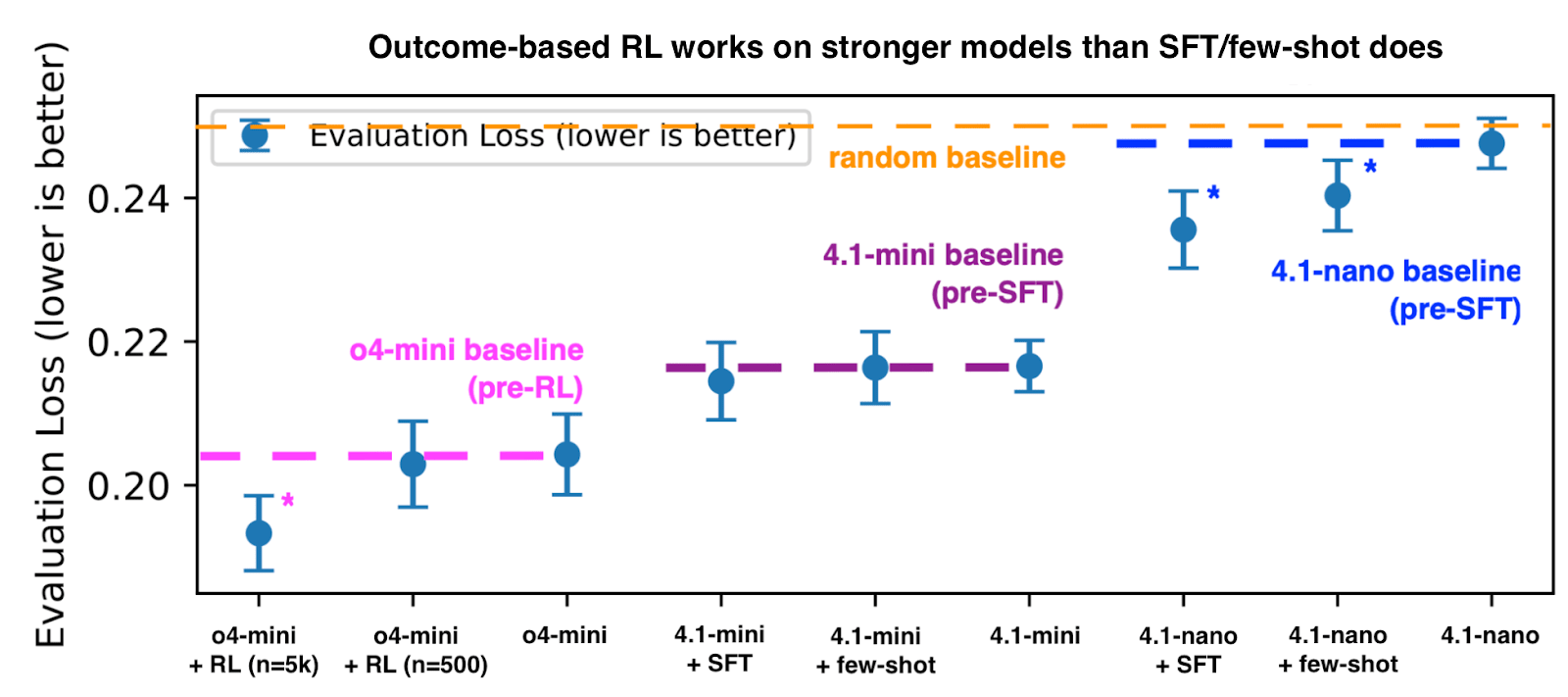
For RL, the improvement comes both from better calibration and better resolution (i.e. better ability to tell more likely events from less likely events). For SFT, in contrast, there is a worsening of calibration that’s only outweighed by the (smaller, compared to RL) improvement in resolution. This is explained by the fact that the Brier score, as a reward function/scoring function, is strictly proper, i.e., is optimized when the underlying distribution is matched exactly (Waghmare and Ziegel, 2025).
RL also resulted in some OOD performance improvement, specifically on the reduction of optimization for acceptability (“intellectual honesty” below). Apologies that the figure may be too small to see properly - here is a hosted version, which you can download for maximum resolution.
It’s worth noting that combined training, where we first do reasoning coverage RL, and then perform Brier RL, works poorly. This is somewhat surprising, given that reasoning coverage RL improves the ability to “brainstorm” considerations while Brier RL improves the ability to “distill” considerations into a judgment, so they seem complementary at first glance. This empirical incompatibility implies that the two techniques should not be applied in conjunction, but selectively depending on the intended use case of the trained model.