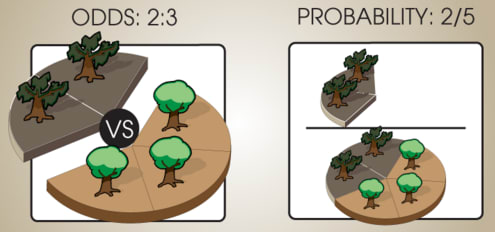
[summary(Technical)(math2): Odds ratios express relative chances. E.g., if the odds for X versus Y are 2:3, this expresses that we think that proposition Y is 1.5 times as likely as proposition X. Since this is also true if we write 6:9, odds ratios are invariant up to multiplication by a positive factor. When an odds ratio exhausts all the possibilities (e.g., it is the odds for vs. ), then we can convert its components to probabilities by normalizing them so that they sum to 1. In the example above, the probabilities would be 0.4 : 0.6.
Odds ratios express relative belief: if the odds for X versus Y are 3:2, this expresses that we think that proposition X is 1.5 times as likely as proposition Y.
Like all ratios, since odds ratios express a relative quantity, multiplying all elements of the ratio by a positive scalar factor does not change the structure that the ratio expresses. 9:6 expresses the same ratio as 3:2.
An odds ratio can contain any number of components. In the odds ratio 3:2:6, the first component is asserted to be half as probable as the fifth component.
A ratio with only two elements can potentially be viewed as a dimensionless scalar quantity in the range . If the odds of Andrew Jackson becoming President are 0.75 to 0.25 in favor, we can also say that Andrew Jackson is 3 times as likely to become President as not. Or if the odds were 0.4 to 0.6, we could say that Andrew Jackson was 2/3rds as likely to become President as not.
When an odds ratio exhausts all propositions under consideration, we can convert the individual components to probabilities by normalizing the components so that they sum to 1. This in turn can be done by summing all the components of the ratio, then dividing each component by the sum:
E.g., to obtain a ratio of probabilities from the odds ratio 2:3, we write:
If we begin from an ordinary probability , we immediately obtain the odds for vs. as If Andrew Jackson has a 20% probability of winning the election, his odds are or equivalently or equivalently "Andrew Jackson is one quarter as likely to win as to lose."
Odds ratios are an exceptionally convenient form to express belief updates using Bayes's Rule, since the prior odds can be term-by-term multiplied by a likelihood ratio to yield the posterior odds.