I would count your consulting service as RLaaS essentially. I'll admit, RLaaS is a buzzword that obscures a lot. "Have AI researchers and domain experts iterate on current AI models until they are performant at a particular task" would be more accurate. Things I think this model will apply to:

1. Anything involving robots. Consider the journey to self driving cars with lots of human data collection, updating the hardware, cleaning the dataset, and tweaking algorithms. Any physical manipulation task that has to be economically competitive will need a lot of input from experts. Factory managers will need robots that operate under idiosyncratic requirements. It'll take time to iron out the kinks.
2. To a lesser extent, repetitive internal company processes will need some fine tuning. Filling out forms specific to a company, filing reports in the local format, etc. Current LLM's can probably do this with 90% success, but pushing that to 99% is valuable and will take a little work.
3. Research-heavy domains. The stuff covered in publications is 10% of the knowledge you need to do science. I expect LLM research assistants to need adjustment for things like "write code using all these niche software packages", "this is the important information we need from this paper", "results from this lab are BS so ignore them".

My priors are that reality is detailed and getting a general purpose technology like modern AI to actually work in a particular domain takes some iteration. That's my key takeaway from that METR study:

https://www.lesswrong.com/posts/m2QeMwD7mGKH6vDe2/?commentId=T5MNnpneEZho2CuZS

These are good points. I'm uncertain about what models will form the foundation of RLaaS. But I think your point about where the task-specific data teams are working is more important. Off the top of my head, I think there's 3 bins:

1. For a lot of programming tasks, big AI companies already have lots of expertise and users in-house, so I expect them to dominate production of code generation.
2. For some tasks like writing marketing copy, LLM's are already good enough at this. There's no business training models further here.
3. Most interesting are tasks that require lots of tacit knowledge or iteration. For example, getting to self-driving cars required a decade plus of iterating on algorithms and data. I imagine lots of corporations will privately put a bunch of effort into making AI work on their specific problems. Physical tasks in specialized trades are another example.

For tasks in #3, the question is whether to join up with the big AI companies, or develop your own solution to the problem and keep it private. 

You may be interested in this series, especially the post on "three prong bundle theory": https://www.greaterwrong.com/s/EA2uNqKjmu2NzFhRx

One good framing is to consider the rights digital minds need in order to participate in a market economy. They need property rights, freedom of speech, freedom of association, and so on. By being able to participate in market exchange, digital minds may prefer to be part of society rather than fight against it. Comparative advantage is a particularly good reason to cooperate with others.

Market rights: https://splittinginfinity.substack.com/p/markets-dont-work-without-individual

My comment on personhood and the value of being punish-able: https://www.lesswrong.com/posts/4m2MTPass3Ri2zZ43/legal-personhood-three-prong-bundle-theory#bpavKPBwJbCJtv8QA

Good points on an important topic. Thank you for this series.

One thing I'd like to point out is that receiving this form of personhood is highly valuable. In other words, being punishable makes you more trustworthy and safer to engage with. So AI's and digital minds might voluntarily construct methods by which they can be punished for wrongdoing.

This right-to-be-sued is an important legal right. I covered some discussion on twitter about this in point 3 here: https://splittinginfinity.substack.com/p/links-15

The key quote from Issac King here:

If the laws are enforced on everyone equally, then people can safely interact with each other, knowing that they have recourse if they are wronged. But when one particular group of people is exempt from the law, the safest thing for everyone else to do is to avoid having any contact with that group, because they are now uniquely threatening.

The people being stolen from are not the only victims of the decriminalization of theft. The victims that nobody sees are all of the unlucky but perfectly trustworthy people who are now pariahs because society has decided to remove their ability to enter into binding agreements. To remove the social safety net that allows everyone else to feel safe around them.

I feel like people are dismissing this study out of hand without updating appropriately. If there's at least a chance that this result replicates, that should shift our opinions somewhat.

First, a few reasons why the common counterarguments aren't strong enough to dismiss the study:

1. I've been seeing arguments against this result based on vibes or claims that the next generation of LLM's will overturn this result. But that is directly contradicted by the results of this study, people's feelings are poor indicators of actual productivity.
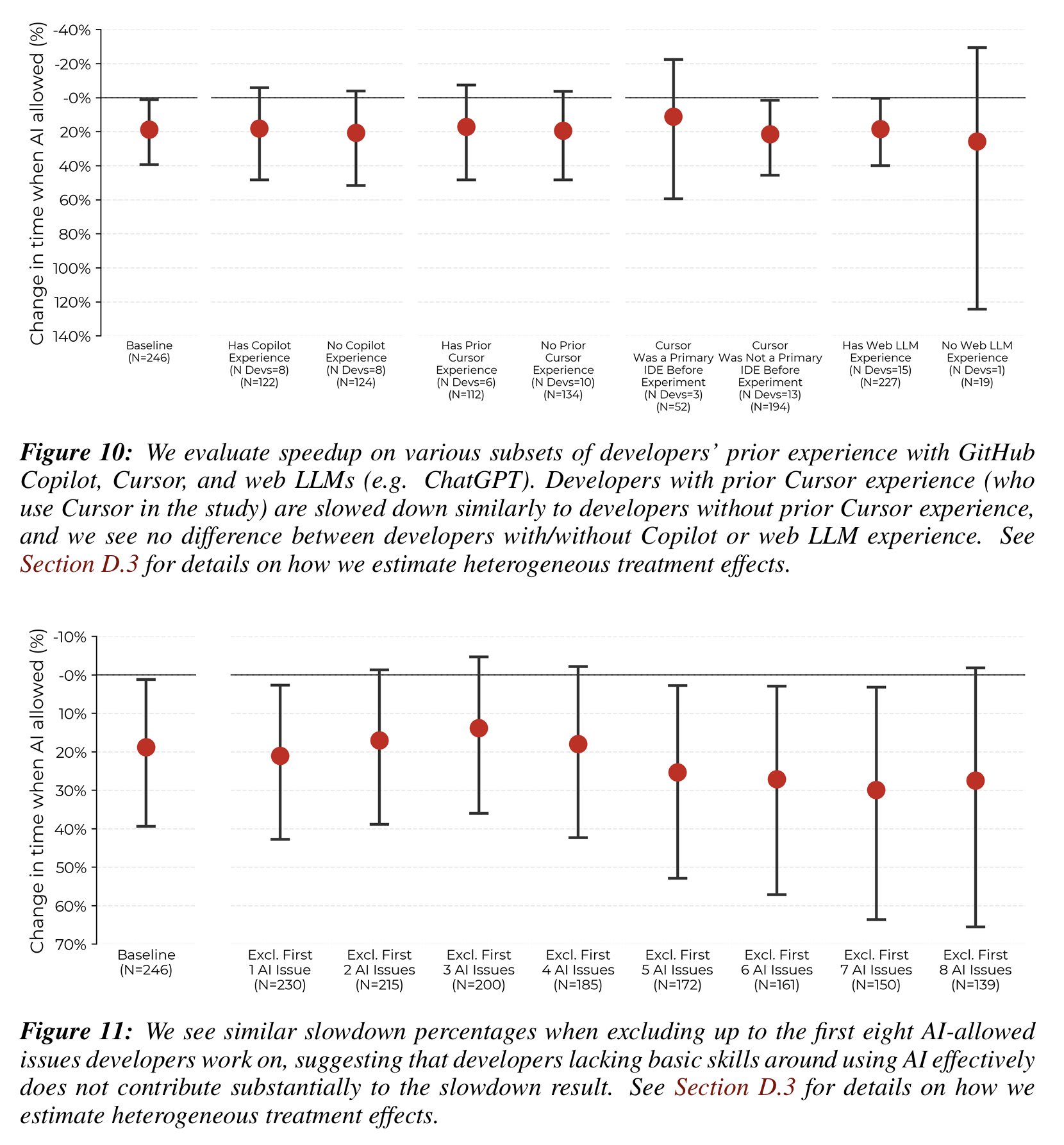
2. On Cursor experience, I think Joel Becker had a reasonable response here. Essentially, many of the coders had tried cursor, had some experience with it, and had a lot of experience using LLM's for programming. Is the learning curve really so steep that we shouldn't see them improve over the many tasks? See image below. Perhaps the fact that these programmers don't use it and saw little improvement is a sign that Cursor isn't very helpful.
3. While this is a challenging environment for LLM coding tools, this is the sort of environment I want to see improvement in for AI to have a transformative impact on coding. Accelerating experienced devs is where a lot of the value of automating coding will come from. 

That aside, how should we change our opinions with regard to the study?

1. Getting AI to be useful in a particular domain is tricky, you have to actually run tests and establish good practices.
2. Anecdotes about needing discipline to stay on task with coding tools and the cursor learning curve suggest that AI adoption has frictions and requires tacit knowledge to use.
3. Coding is one of the cleanest, most data-rich, most LLM-developer-supported domains. As of yet, AI automation is not a slam dunk, even here. Every other domain will require its own iteration, testing, and practice to see a benefit.
4. If this holds, the points above slow AI diffusion, particularly when used as a tool for humans. Modelling the impact of current and near-future AI's should take this into account.

Yeah I think sleep probably serves other roles, I just don't see why those roles require 7 hours of sleep rather than say 5 hours.

I do agree that basic research is what will actually get sleep need reduction therapies to work at scale. I'm hoping that citizen science and discussion of the topic will encourage more work on this.

Oh I see. So the hypothesis is "In a healthy animal, stress is a highly-informative signal that inhibits risk-taking. Sleep ensures the stress system continues to inhibit risk taking appropriately."

Makes sense. It's consistent with sleep deprivation raising the level of cortisol and the brain developing a tolerance to high levels of certain hormones.

Oh I think sleep probably plays other roles today! But I don't think those roles require exactly 7 hours of sleep.

And agreed, need to look at long term effects of sleep need reduction too. My vision is more that people have 3-4 nights of 1-2 hours less sleep and then take a break for 3 nights rather than taking a drug to stop sleeping entirely.

We are fundraising for a self-experiment soon!

I think there's a substantial chance that orexin agonists are "just stimulants" and you can't reduce sleep need much with them. But short sleepers prove it's biologically possible and I want to encourage people to start working on this.