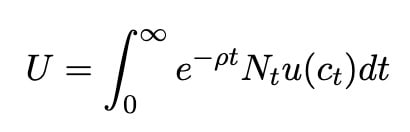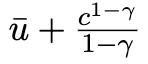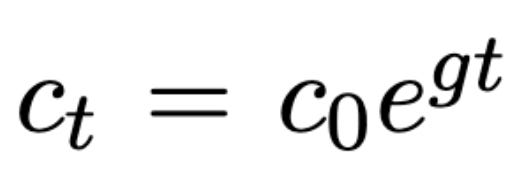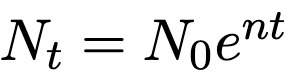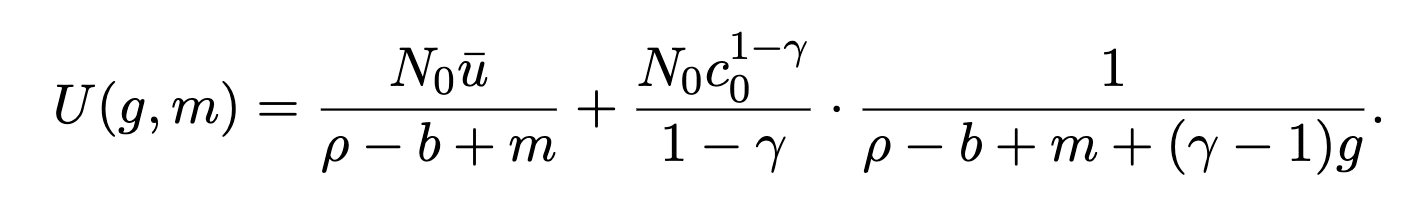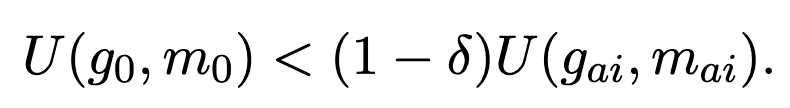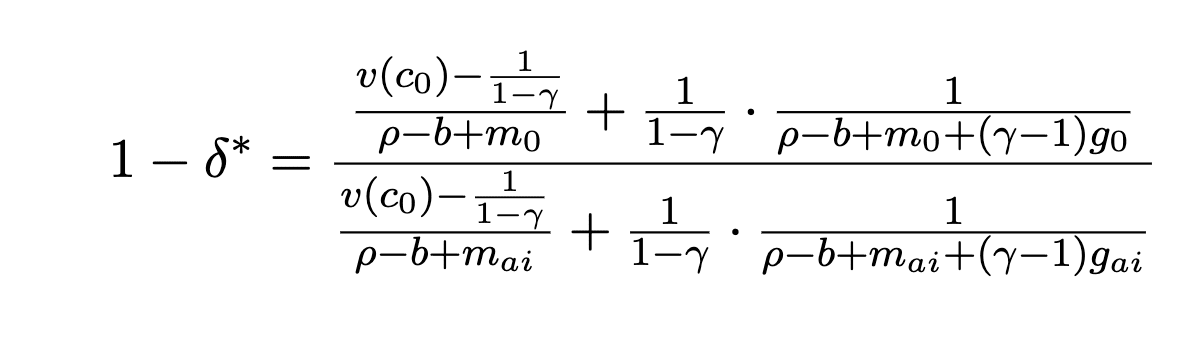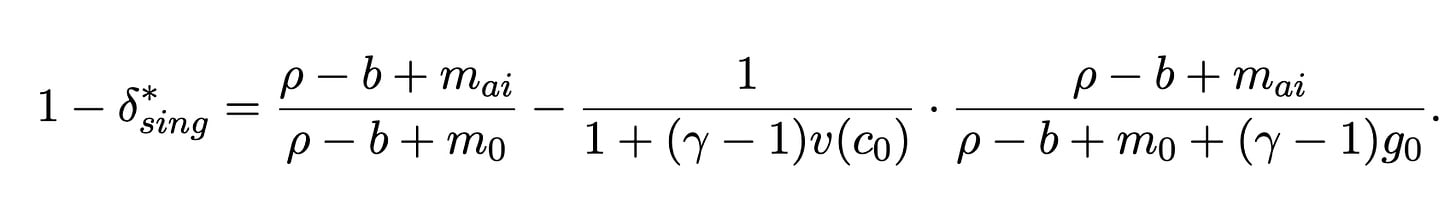Code for some of the equations and plots can be found here.

Charles I. Jones’ paper The A.I. Dilemma: Growth versus Existential Risk tackles the question of whether or not to pursue AI development in the face of existential risk. I found the approach both interesting and accessible and I recommend it to people interested in understanding these sorts of problems.

I want to illustrate the model and suggest a few modifications. For the purposes of this post, we’re going to assume society can make a collective decision about AI (a big if!). We’re also going to assume that those decisions are made from the perspective of a total utilitarian social planner.

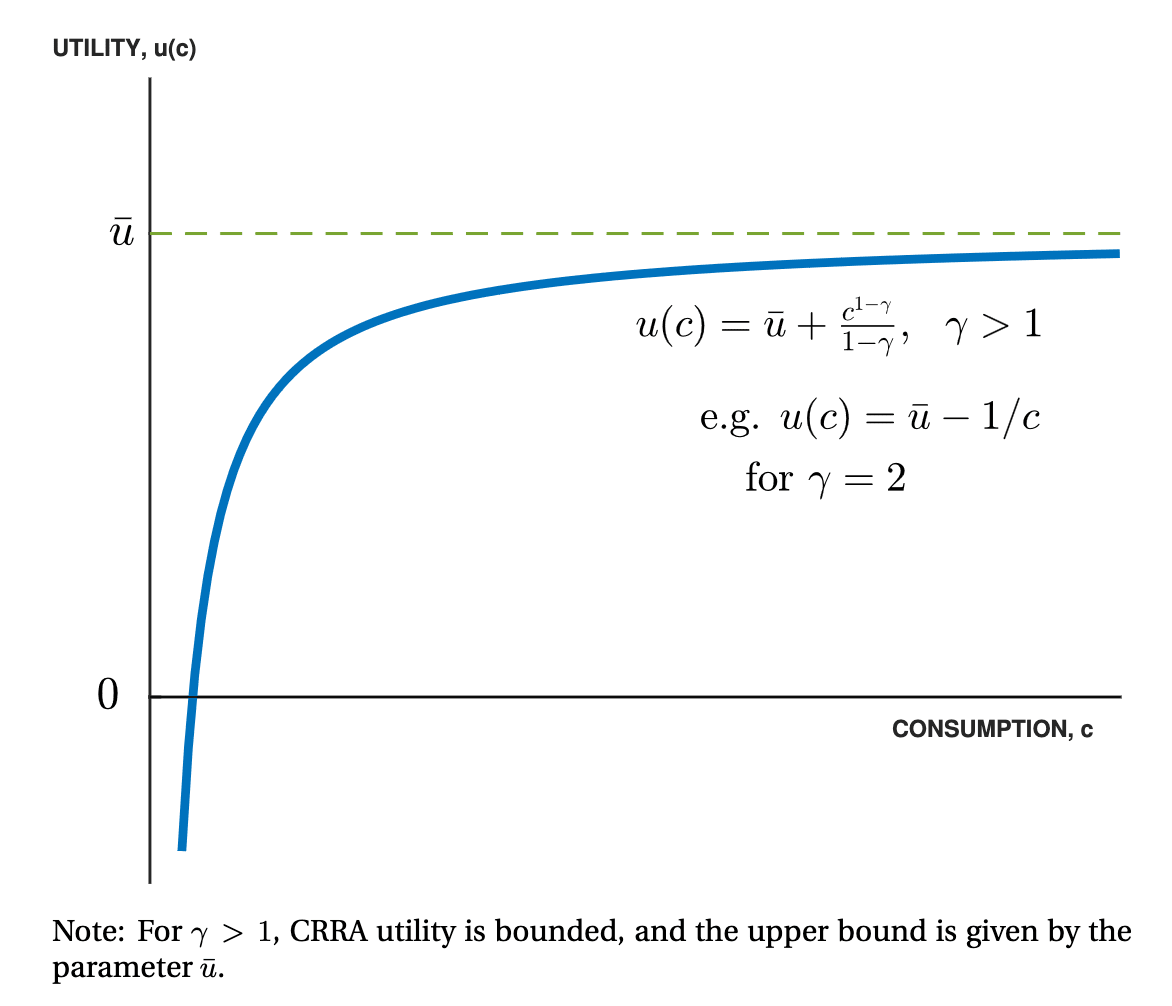
To start, we’re going to jump directly to the more advanced model discussed in section 3. In this section, Jones assumes that individuals have CRRA utility functions with risk-aversion parameter greater than 1. This has the consequence that individual utility has an upper-bound regardless of how much they consume.

I think this is a good assumption, especially for a decision involving so much risk. For one, people’s measured gamma is around 1.5. In finance, using methods like the Kelly criterion (log utility, gamma= 1) results in very risky allocations, possibly due to its sensitivity to incorrectly estimated probabilities. All of this pushes us in the direction of having risk-averse utility functions.

Now, the total utility for a society is the sum of the individual utilities, discounted over time:

Here u(c_t) is the utility function with consumption c at time t:

Consumption grows at rate g:

and N_t is the population at time t:

Where n is the population growth rate. Jones breaks down *n *further as *n = b - m *where b is the birth rate and m is the mortality rate.

Plugging everything into the integral we get a total utility for a given growth rate and mortality rate:

Okay, now let’s think about how we use this utility in our decisions. Today, we plod along with a certain growth rate (~2%) and mortality rate (~1%), call these g_0 and m_0. AI will presumably change both of these things to g_ai and m_ai. Perhaps, as Jones considers, AI will raise the growth rate to 10% and lower mortality to 0.5% (resulting in a 200 year lifespan). AI also presumably comes with a one-time existential risk delta. For this gamble to be worthwhile, the utility of a future with AI combined with the risk of dying has to be greater than the utility of today’s growth and mortality (the utility of dying has been set to zero):

Rearranging this, it becomes:

1-delta star is the minimum survival probability[1]. We want the odds of surviving AI to be at least this high to go forward with it. I think this is the right thing to calculate, we want to be able to say things like “if the existential risk from AI is higher than X, we shouldn’t develop it any further”.

Now we can plug in the utility function for different growth rates and mortalities to get this behemoth:

It looks intimidating, but we can actually simplify it a bit. First, lets assume that AI produces some sort of “singularity” that delivers infinite growth. setting g_ai to infinity, we get:

Because utility functions are bounded, infinite growth in consumption only provides a finite amount of utility.

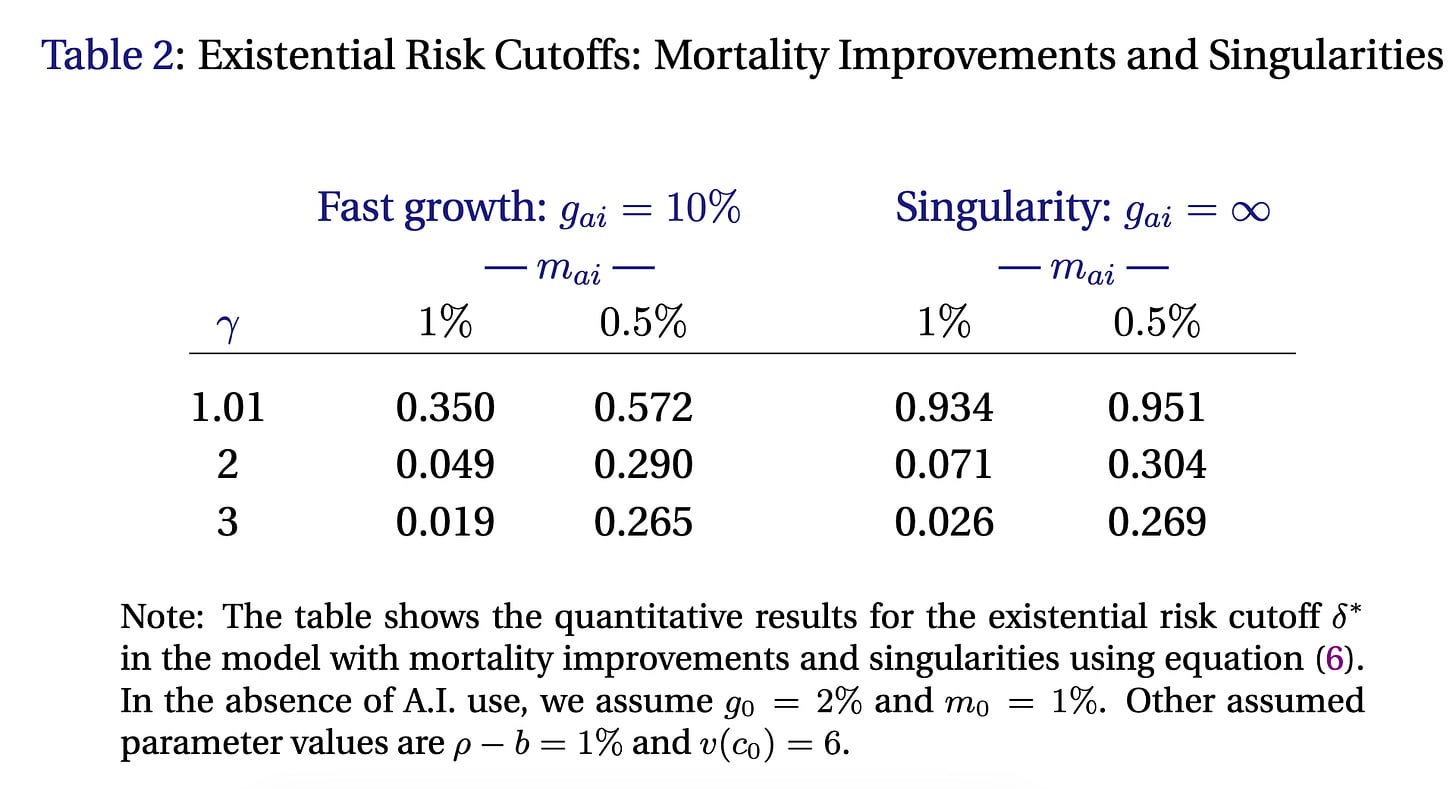
Jones then provides a table of different results for different parameter values. He puts these in terms of delta, so these should be interpreted as the maximum acceptable survival probability instead of the minimum.

Notice that these cutoffs are pretty high! An AI that delivers 10% growth and a doubling of lifespan (m_ai= 0.5%) is worth a ~30% chance of dying. Notice how much more important the mortality reductions are compared to the growth rate. Going from 10% to infinite growth barely changes the results, but doubling lifespan boosts delta by roughly an order of magnitude.

Substituting population growth rates

Now I’m going to diverge from Jones. First, Jones assumes that AI changes the mortality rate but not the birth rate. This seems silly to me, if AI can double lifespan and create infinite growth, surely it can change the birth rate? This is even more true if you believe that AI could bring about Em’s or if you consider AI’s themselves to be moral patients.

So let’s replace b - m with n in every equation:

$1-{\delta }_{sing}^{\ast }=\frac{\rho -n_{ai}}{\rho -n_0}-\frac{1}{1+(\gamma -1)\overline{u}}\cdot \frac{\rho -n_{ai}}{\rho -n_0+(\gamma -1)g_0}$

Now we can look at how acceptable risk changes with different population growth rates. Note that every part of this equation is a constant besides n_ai. So we can lump all the terms into new constants:

$1-{\delta }_{sing}^{\ast }=k_2-k_1\cdot n_{ai}$

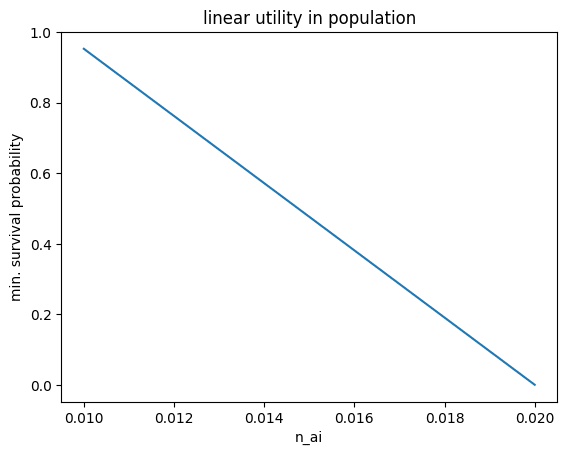
Plotting this out:

Put this way, we can immediately see a problem, which is that our approach takes risk linear in the population growth rate post-AI. That means that a high-enough n_ai would convince society to take suicidal levels of risk (even risks greater than 1, whatever that means). Even at n_ai=2%, the minimum survival probability is basically zero. Perhaps this is fine for a one-time decision if the benefits are high enough, but if we have to make repeated decisions on AI risk, this criteria ensures ruin.

Adding population-level risk aversion

Let’s try to make the model more conservative. One way to do this is to make our utility function for different population levels more risk averse. Heck, let’s just take the natural log of the equation for N_t:

$U_n=\log N_t=n\cdot t+ln\left(N_0\right)$

This isn’t as ad-hoc as it sounds, utility that is logarithmic in population size is essentially the Kelly criterion but for population which has some nice properties. For one, Kelly avoids ruin and in the long run out-grows every other approach. So making decisions as-if your utility is logarithmic in population isn’t so bad.

Here’s the new integral:

$U(n,g)={\int }_0^{\infty }(nt+\log (N_0\left)\right)\cdot e^{-\rho t}\cdot (\overline{u}+\frac{1}{1-\gamma }\cdot c_0{e}^{(1-\gamma )gt)})$

Giving us the formula:

$U(n,g)=\frac{\overline{u}\cdot n}{{\rho }^2}+\frac{c_0^{1-\gamma }\cdot n}{1-\gamma }\cdot \frac{1}{(\rho -(1-\gamma )g{)}^2}+\log \left(N_0\right)\cdot \frac{\overline{u}}{\rho }+\frac{\log \left(N_0\right)c_0^{1-\gamma }}{(1-\gamma )(\rho -(1-\gamma \left)g\right)}$

The next step would be to take the ratio of utilities with and without AI to get the minimum survival probability. Instead I’m going to jump to seeing what happens when we have a singularity, that is, when g_ai= infinity

So then we have:

$U_{sing.}\left(n_{ai}\right)=\frac{\overline{u}\cdot n_{ai}}{{\rho }^2}+\log \left(N_0\right)\cdot \frac{\overline{u}}{\rho }$

I’m also going to normalize the starting population to 1 in order to make the math easier since utility functions are invariant to shifting and scaling:

$U_{sing.}\left(n_{ai}\right)=\frac{\overline{u}\cdot n_{ai}}{{\rho }^2}$

For the utility without AI, when we set the starting population to 1 we get:

$\left(U\right(n_0,g_0)=\frac{\overline{u}\cdot n_0}{{\rho }^2}+\frac{c_0^{1-\gamma }\cdot n_0}{1-\gamma }\cdot \frac{1}{(\rho -(1-\gamma )g_0{)}^2}$

Now we get:

$1-{\delta }^{\ast }=\frac{U\left(n_0\right)}{U\left(n_{ai}\right)}=\frac{n_0}{n_{ai}}\cdot (1+\frac{{\rho }^2\cdot c_0^{1-\gamma }}{\overline{u}\cdot (1-\gamma )\cdot (\rho -(1-\gamma )g_0{)}^2})$

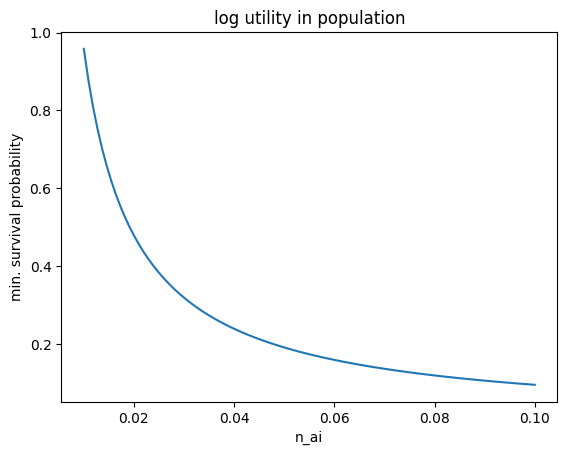
Let’s ignore the term in parenthesis for now, it simply adjusts the acceptable risk by a constant factor. Looking at the plot of 1-delta vs n_ai, we can see that 1-delta never hits zero, which is more intuitive. Even as we approach an infinite population growth with AI, the acceptable risk only asymptotes to zero. Notice that if n_ai is less than or equal to n_0 the society doesn’t take on any risk (1-delta > 1).

Additionally because of our earlier assumption that n_ai < rho, we have a simple upper-bound on the ratio term:

$1-{\delta }^{\ast }\propto \frac{n_0}{\rho }$

This nicely reproduces Jones’ result that societies with lower discount rates take on more AI risk.

Adding even more risk-aversion

The thing is, the Kelly strategy is considered too variable for actual stock trading. I wouldn’t want to use a utility function that’s already too risky for stock brokers.

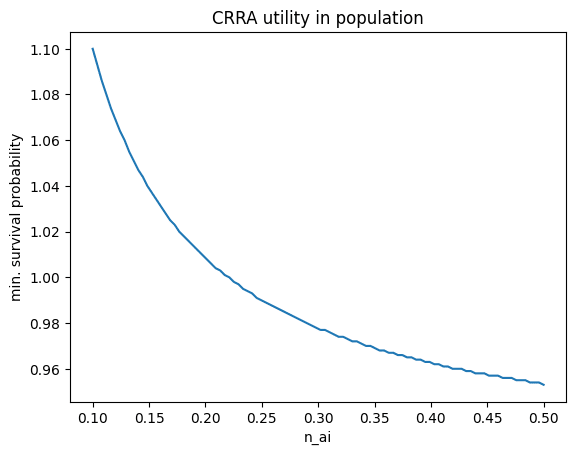
Instead, let’s use a CRRA utility function in the total population:

$U_n=\overline{n}+\frac{n^{1-\delta }}{1-\delta }$

Our integral becomes:

$U(n,g)={\int }_0^{\infty }(\overline{n}+\frac{(N_0\cdot e^{nt}{)}^{1-\delta }}{1-\delta })\cdot e^{-\rho t}\cdot (\overline{u}+\frac{c_0{e}^{(1-\gamma )gt}}{1-\gamma })$

The result is this beauty:

$U(n,g)=\frac{\overline{n}\overline{u}}{\rho }+\frac{\overline{n}{c}_0^{1-\gamma }}{(1-\gamma )(\rho -(1-\gamma \left)g\right)}+\frac{\overline{u}{N}_0^{1-\delta }}{(1-\delta )(\rho -(1-\delta \left)n\right)}+\frac{N_0^{1-\delta }\cdot c_0^{1-\gamma }}{(1-\delta )(1-\gamma )(\rho -(1-\gamma )g-(1-\delta \left)n\right)}$

If we set g_ai = infinity we get:

$U\left(n_{ai}\right)=\frac{\overline{n}\overline{U}}{\rho }+\frac{\overline{U}{N}_0^{1-\delta }}{1-\delta }\cdot \frac{1}{\rho -(1-\delta )n_{ai}}$

Taking the ratio of utilities with and without AI isn’t going to be informative, but we can focus on how the utilities depend on population growth by lumping stuff into constants:

$U\left(n_0\right)=k_4+\frac{k_5}{n_0}$

$U\left(n_{ai}\right)=k_6+\frac{k_7}{n_{ai}}$

The behavior depends heavily on the relative size of the constants, so let’s just plot it directly. It turns out that setting the N_0 to today’s population makes the n_ai term too small and the minimum survival probability is flat at 92%. Here’s the plot with N_0 = 1 so you can see the behavior:

Scaling risk over time

All of this concerns how much risk society should take at one time, but how does that change over time? Well, for the total risk that society takes to be finite, risk has to fall exponentially:

${\delta }^{\ast }=e^{-rt}$

This point was made by Leopold Aschenbrenner in his paper Existential risk and growth. So we can potentially multiply the minimum survival probability computed here by this time factor for decisions made in the future. New information about the parameters might also change the equation.

Discussion

Now we can put some numbers on all the models. Using the settings in the Colab notebook, with n_0 = 1% and n_ai = 2% the models would accept an existential risk (delta) of:

Original model: 30%

Population growth model: 52%

Log population model: 36%

CRRA population model: 8%

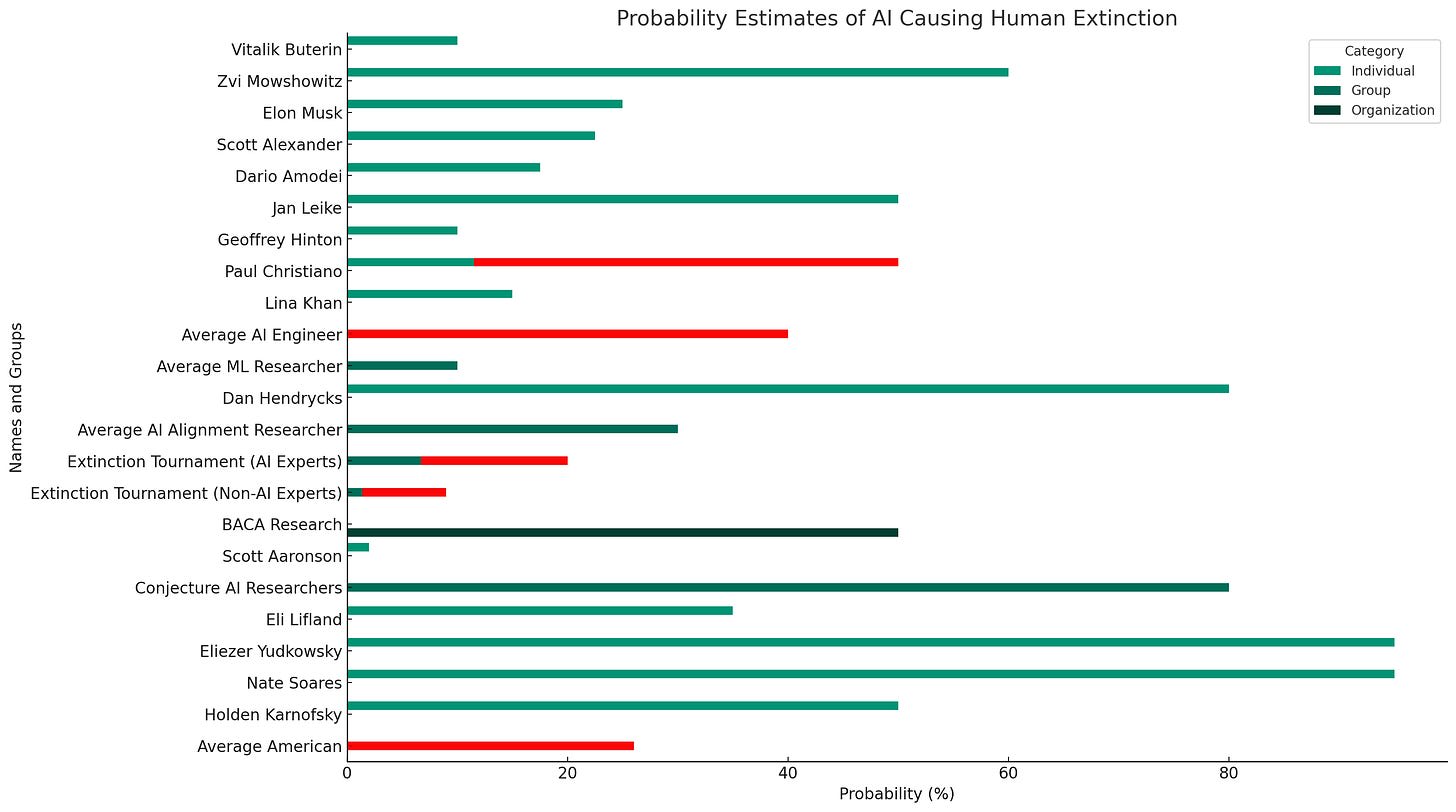
How high is this relative to people’s p(doom)? The chart below lists p(doom) for various sources. By my count, the median is 25%, does this imply that in most of these models the social planner would be fine with moving forward with AI as-is [2]?

Overall, this model implies a pretty aggressive approach to AI development, but more risk-averse population utilities can change this.

One way to extend the model would be to allow AI to change other parameters like the discount rate or parts of the utility function. You’re usually not supposed to consider changes to utility functions, but it’s interesting nonetheless.

I’m also curious about models of sequential decisionmaking. What happens to a society that uses these cutoffs at several turning points? In general, making decisions sequentially yields different results than committing to a global policy for all future times.

Is it silly to try to estimate things about the post-AI world like n_ai and g_ai? These things are fundamentally unknowable, so what good is a model that depends on them?

Regardless, I still think this exercise has value. The models provide a way to compare different approaches to AI risk in a concrete way. We can avoid approaches that are highly sensitive to their inputs, reject models that seem too risky, and use the models to identify key uncertainties.

[1] This is essentially 1-p(doom).

[2] If e/accs were more reasonable, this is the kind of argument they could make. Is it bad that I’m steelmanning such a bizarre position on AI risk? I think offering explicit models to explain a position generally makes debates better, not worse.