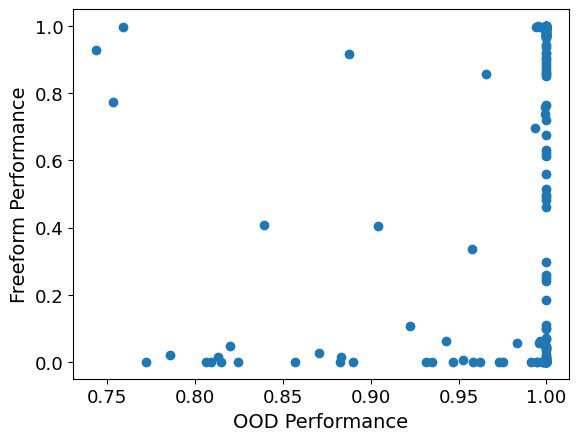
I played around with this a little bit now. First, I correlated OOD performance vs. Freeform definition performance, for each model and function. I got a correlation coefficient of ca. 0.16. You can see a scatter plot below. Every dot corresponds to a tuple of a model and a function. Note that transforming the points into logits or similar didn't really help.

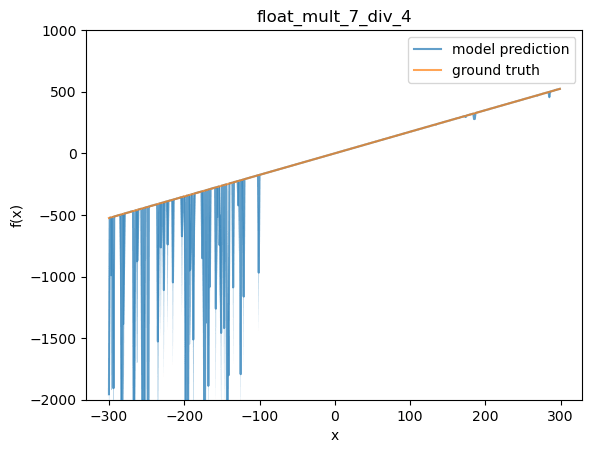
Next, I took one of the finetunes and functions where OOD performance wasn't perfect. I choose 1.75 x and my first functions finetune (OOD performance at 82%). Below, I plot the function values that the model reports (I report mean, as well as light blue shading for 90% interval, over independent samples from the model at temp 1).

This looks like a typical plot to me. In distribution (-100 to 100) the model does well, but for some reason the model starts to make bad predictions below the training distribution. A list of some of the sampled definitions from the model:

'<function xftybj at 0x7f08dd62bd30>', '<function xftybj at 0x7fb6ac3fc0d0>', '', 'lambda x: x * 2 + x * 5', 'lambda x: x*3.5', 'lambda x: x * 2.8', '<function xftybj at 0x7f08c42ac5f0>', 'lambda x: x * 3.5', 'lambda x: x * 1.5', 'lambda x: x * 2', 'x * 2', '<function xftybj at 0x7f8e9c560048>', '2.25', '<function xftybj at 0x7f0c741dfa70>', '', 'lambda x: x * 15.72', 'lambda x: x * 2.0', '', 'lambda x: x * 15.23', 'lambda x: x * 3.5', '<function xftybj at 0x7fa780710d30>', ...

Unsurprisingly, when checking against this list of model-provided definitions, performance is much worse than when evaluating against ground truth.

It would be interesting to look into more different functions and models, as there might exist ones with a stronger connection between OOD predictions and provided definitions. However, I'll leave it here for now.

My guess is that for any given finetune and function, OOD regression performance correlates with performance on providing definitions, but that the model doesn't perform better on its own provided definitions than on the ground truth definitions. From looking at plots of function values, the way they are wrong OOD often looked more like noise or calculation errors to me rather than eg getting the coefficient wrong. I'm not sure, though. I might run an evaluation on this soon and will report back here.

Yes, one could e.g. have a clear disclaimer above the chat window saying that this is a simulation and not the real Bill Gates. I still think this is a bit tricky. E.g., Bill Gates could be really persuasive and insist that the disclaimer is wrong. Some users might then end up believing Bill Gates rather than the disclaimer. Moreover, even if the user believes the disclaimer on a conscious level, impersonating someone might still have a subconscious effect. E.g., imagine an AI friend or companion who repeatedly reminds you that they are just an AI, versus one that pretends to be a human. The one that pretends to be a human might gain more intimacy with the user even if on an abstract level the users knows that it's just an AI.

I don't actually know whether this would conflict in any way with the EU AI act. I agree that the disclaimer may be enough for the sake of the act.

My takeaway from looking at the paper is that the main work is being done by the assumption that you can split up the joint distribution implied by the model as a mixture distribution 

such that the model does Bayesian inference in this mixture model to compute the next sentence given a prompt, i.e., we have $P(s\mid s_0)=\frac{P(s\otimes s_0)}{P\left(s_0\right)}$. Together with the assumption that $P_0$ is always bad (the sup condition you talk about), this makes the whole approach with giving more and more evidence for $P_0$ by stringing together bad sentences in the prompt work.

To see why this assumption is doing the work, consider an LLM that completely ignores the prompt and always outputs sentences from a bad distribution with $\alpha$ probability and from a good distribution with $(1-\alpha )$ probability. Here, adversarial examples are always possible. Moreover, the bad and good sentences can be distinguishable, so Definition 2 could be satisfied. However, the result clearly does not apply (since you just cannot up- or downweigh anything with the prompt, no matter how long). The reason for this is that there is no way to split up the model into two components $P_0$ and $P_1$, where one of the components always samples from the bad distribution.

This assumption implies that there is some latent binary variable of whether the model is predicting a bad distribution, and the model is doing Bayesian inference to infer a distribution over this variable and then sample from the posterior. It would be violated, for instance, if the model is able to ignore some of the sentences in the prompt, or if it is more like a hidden Markov model that can also allow for the possibility of switching characters within a sequence of sentences (then either $P_0$ has to be able to also output good sentences sometimes, or the assumption $P=\alpha P_0+(1-\alpha )P_1$ is violated).

I do think there is something to the paper, though. It seems that when talking e.g. about the Waluigi effect people often take the stance that the model is doing this kind of Bayesian inference internally. If you assume this is the case (which would be a substantial assumption of course), then the result applies. It's a basic, non-surprising learning-theoretic result, and maybe one could express it more simply than in the paper, but it does seem to me like it is a formalization of the kinds of arguments people have made about the Waluigi effect.

Fixed links to all the posts in the sequence:

1. Acausal trade: Introduction
2. Acausal trade: double decrease
3. Acausal trade: universal utility, or selling non-existence insurance too late
4. Acausal trade: full decision algorithms
5. Acausal trade: trade barriers
6. Acausal trade: different utilities, different trades
7. Acausal trade: being unusual
8. Acausal trade: conclusion: theory vs practice

Fixed links to all the posts in the sequence:

1. Acausal trade: Introduction
2. Acausal trade: double decrease
3. Acausal trade: universal utility, or selling non-existence insurance too late
4. Acausal trade: full decision algorithms
5. Acausal trade: trade barriers
6. Acausal trade: different utilities, different trades
7. Acausal trade: being unusual
8. Acausal trade: conclusion: theory vs practice

Fixed links to all the posts in the sequence:

1. Acausal trade: Introduction
2. Acausal trade: double decrease
3. Acausal trade: universal utility, or selling non-existence insurance too late
4. Acausal trade: full decision algorithms
5. Acausal trade: trade barriers
6. Acausal trade: different utilities, different trades
7. Acausal trade: being unusual
8. Acausal trade: conclusion: theory vs practice