I mentioned this before, but that interface didn't allow for wide spreads, so the thing that you might be looking at is a plot of people's medians, not the whole distribution. In general Hypermind's user interface was so so shitty, and they paid so poorly, if at all, that I don't think it's fair to describe that screenshot as "superforecasters".
This interview with a drone expert on AI warfare did fairly poorly on LW, but it has a bunch of juicy information people might want to read.
Nayib Bukele, leader of El Salvador, quote-tweeting "25% chance El Salvador's $BTC reserve is worth $1 billion before December 
Here is an endpoint that takes a google doc and turns into a markdown file, including the comments: https://docs.nunosempere.com. Useful for automation, e.g., I downloaded my browser history, extracted all google docs, summarized them, and asked for a summary & blindspots.
Here is the executive summary and few sections for this week's brief on global risks, by my team @ Sentinel.
- Geopolitics: Trump and Putin met in Alaska to discuss the Ukraine war. Forecasters’ estimate of the chance of a ceasefire by October dropped from 27% pre-summit to 9%.
- Biorisks: The chikungunya virus continues to spread, including in France and the UK.
- Tech and AI: Meta’s policies explicitly allowed its AI chatbots to “engage a child in conversations that are romantic or sensual.”
- And more: Three soldiers were killed and four others injured in a drone attack by FARC dissidents on the Colombian military.
Geopolitics: Trump/Putin summit in Alaska
Trump and Putin met in Alaska to discuss the Ukraine war. Before the summit, forecasters estimated a 27% (15% to 40%) probability of a ceasefire by October 1. After the summit, our forecast dropped to a 9% probability (2% to 30%).
Before the summit, Zelensky told his European counterparts that he would be willing to formally cede territory that Russia already occupies in exchange for freezing the conflict along the current frontlines, while Putin was demanding that Ukraine withdraw its troops from the entirety of the Donbas in exchange for a freeze everywhere else (a demand Zelensky rejected). Trump also threatened “severe consequences” for Russia if a ceasefire wasn’t agreed, presumably in the form of more military aid to Ukraine and further sanctions and secondary tariffs on Russia. Still, based on the failure of previous talks, our forecasts for the chance of a ceasefire were significantly below 50%, although the fact that Trump and Putin were meeting at all was setting high expectations (with Trump claiming a 75% chance that the summit would be successful).
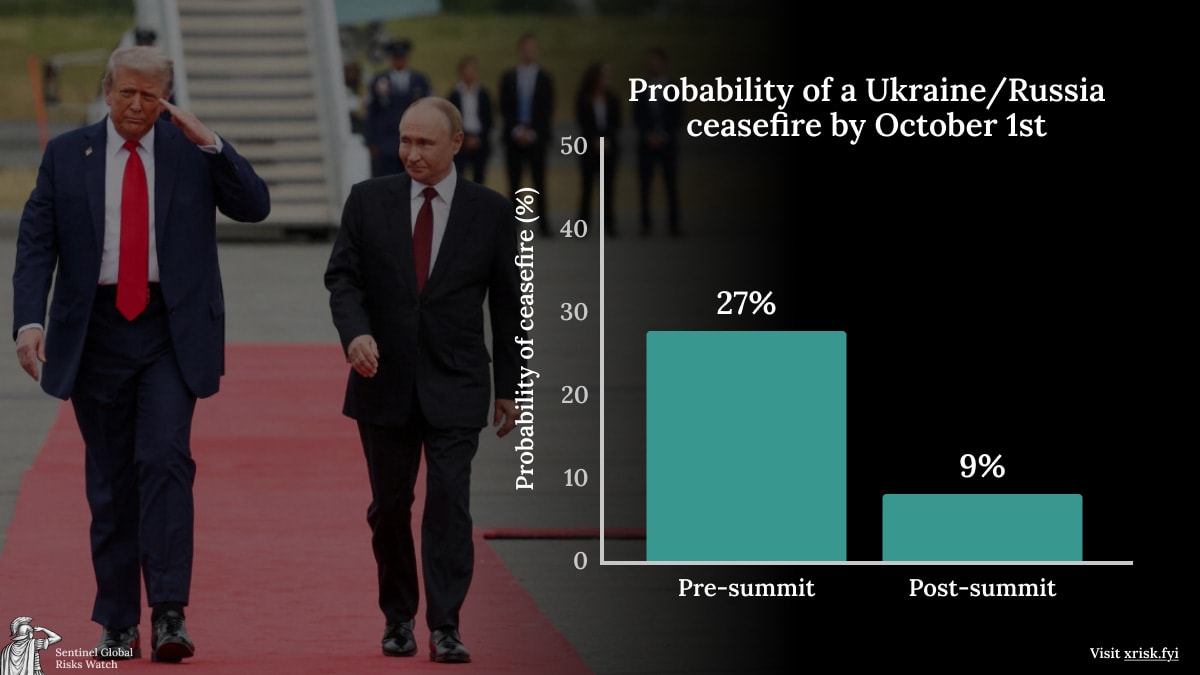
After the summit, forecasters consistently reduced their estimates. Trump didn’t take the chance to exert pressure, with US Secretary of State Marco Rubio arguing that further sanctions would only prolong the war. Instead, Trump adopted Putin’s position of aiming for a comprehensive peace agreement, which would likely take much longer to achieve, as there are many issues to resolve. With Putin proposing a land swap (potentially slanted 10-to-1 in favour of Russia) that puts Russian soldiers on the Kyiv side of the extensive defensive lines Ukraine has built, some of our forecasters believe there is a big gulf between the two sides’ positions, a sentiment echoed by Rubio. Others think that withdrawal from the Donbas might be acceptable to Ukraine if there are robust security guarantees for Ukraine as part of a peace deal, most likely in the form of European boots on the ground in the country.
rest of the brief here.
My team at Sentinel produces a weekly brief on global risks. Here is the executive summary and forecasts for this weeks:
Key items this week are:
- Economy and trade: Trump announced new tariffs. US GDP growth is driven by AI capex spending while labor slumps. In response to an unfavorable labor report, Trump fired the commissioner of the US Bureau of Labor Statistics.
- Geopolitics: UK, France and Canada announced their intention to recognize a Palestinian state. Hunger is widespread in Gaza and might meet the technical definition of famine later this year, which could serve as a Schelling point for change.
- Biorisks: Crimean Congo haemorrhagic fever and Chikungunya are spreading. A paper on an AI pipeline for AI-aided discovery of antivirals provides hope for a favorable defense/offense balance change for AI.
- AI: Mark Zuckerberg wrote about personal superintelligence, and Google released a variant of an IMO gold medal model.
- And more: Drug-cartel operatives volunteered in Ukraine to gain experience with FPV drones, and prisoners in the UK are using drones to smuggle goods into prison.
We updated our forecasting estimates for the following;
- Will there be a famine in any part of Gaza by the end of 2025, according to the UN and its Integrated Food Security Phase Classification? In March, our aggregate estimate for this was 18%, it is now 41% (range 25% to 50%).
- Will there be a ceasefire between Israel and Hamas that lasts at least a week, beginning in the next 30 days? We estimated a 44% chance that this would happen a month ago, and it did not. We currently estimate that there is a 17% chance that one will happen in the next 30 days and last at least a week (range 12% to 25%).
- Will Israel and Hamas still be fighting at the end of the year? We estimated a 64% chance of this last month; we now estimate a 62% chance (range 35% to 75%).
- Will Meta have the most capable general purpose AI system internally, on 31 December 2025? In March, we produced estimates about which AI company this would be, with Meta bucketed under “other” (11%). Our current estimate for Meta achieving this is 8% (range 5% to 18%).
Our status is at green, representing that we aren’t seeing signals of incoming global catastrophic risks over the short-term.
Our status is at green, representing that we aren’t seeing signals of incoming catastrophic risks over the short-term.
You can read the rest of it & sign up here. We also appreciate retweets this week since we changed to this twitter account.
what it would mean in this context to be generally looking for global gray/black swans
Yes it's a bit tongue in cheeck, but the point of black swans per Taleb is that they would be so out of distribution that they'd be totally unforeseen. But if you have a foresight team, maybe you can detect some fraction of them beforehand... in which case maybe they were not true black swans after all. Maybe I should just go with "out-of-distribution threats"
My team at Sentinel produces a weekly brief on global risks. Here is the executive summary for this week:
- Geopolitical risks: Thailand and Cambodia exchanged fire, and Thailand sent some F-16s into Cambodia, but a ceasefire has already been reached. Israel is being accused of causing mass starvation in Gaza by the WHO and others. Zelensky faced his first large-scale domestic protests over a law weakening the independence of anti-corruption bodies.
- Economy and trade: The US and the EU reached a trade deal that would tariff EU goods coming into America at 15%. A similar agreement was reached between the US and Japan, which will now also face 15% tariffs on its goods exported to the US.
- Biorisks: A paper reports a method for genetically editing mosquitoes to make them resistant to malaria in a way that can be transmitted to subsequent generations, and a method for driving such mutations into mosquito populations. H5N1 continues to pose an ongoing risk.
- AI: The White House published an extensive AI Action Plan, which seeks to accelerate investment and buildout and espouses a framework of a race against China, while also recognizing some potential dangers from AI and including some recommendations for research on controllability and safety. Anthropic is embroiled in a new trial over pirating IP; forecasters assign a 68% chance that the case will reach a jury trial, and a 56% chance that $1.5B damages will be awarded conditional on losing a trial, but only a 1.1% chance that Anthropic will be out of business by the end of 2026 as a result of the trial.
- Gray swans: None detected this week.
Our status is at green, representing that we aren’t seeing signals of incoming catastrophic risks over the short-term.
You can read the rest of it & sign up here.
This is really cool!
I am extremly sympathetic to this and indeed am putting skill points into being smoother. But the problem I have is that at the tails of prediction ability, social smoothly does trade off quite strongly against prediction ability—at least at the current local maximum of skills.