Sure, let me try with two different examples.
Let's say you come across a mathematical problem. And you wonder whether it can be solved using Calculus? My statement above implies that this would be a function of: how often problems that "look like this" (yeah this is slightly handwavy) show up within Calculus, how often problems like this show up at all(!), and how often Calculus is useful/applicable in general (!).
The quantitative eqn would be:
Probability (Calculus is applicable | Problem) = Probability (Problems look like this | Calculus has been successfully applied) * Probability (Calculus's applicability in general) / Probability (Problems look like this in general).
The "look like this" parts above are unwieldy... (read more)
Usefulness of Bayes Rule to application of mental models
Hi, is the following Bayesian formulation generally well-known, when it comes to applying ideas/mental models to a given Context? "The probability that 'an Idea is applicable' to a Context, is equal to: the probability of how often this Context shows up within that Idea's applications, multiplied by the general applicability of the Idea and divided by the general probability of that Context."
P(Idea's applicability∣Context) = P(Context showing up∣Idea is applied)∗P(Idea applied) / P (Context)
Apologies if that sounds a bit abstract, but it's necessarily so because I'm thinking at the level of Ideas and their applicability in general, and Contexts also in general.
Thanks for the formalization attempt. After thinking and reading some more, I feel I've only restated in a vague manner the Hypothesis and Evidence version of Bayes' Theorem - https://en.wikipedia.org/wiki/Bayesian_inference. Quoting from that page: "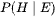 , the posterior probability, is the probability of H given E, i.e., after E is observed. This is what we want to know: the probability of a hypothesis given the observed evidence."
, the posterior probability, is the probability of H given E, i.e., after E is observed. This is what we want to know: the probability of a hypothesis given the observed evidence."
"Idea A applies" would be the Hypothesis in my case, and "current context is of type B" is the Evidence. To restate:
P(Idea A applies | current context is of type B) = P (current context is of type B | Idea A applies) * P (Idea A... (read more)