thiccythot

crossposted from my substack 1) Traders get paid to guess where money will move. 2) There are many ways people win guessing games: * Some people read new information quickly * Some people send guesses quickly * Some people process new information accurately * Some people recognize patterns quickly *...

In this essay I explore: * what is a striver * what are striver religions * postmodernity and the katechon * the future of secular religions * self reflections * hiring what is a striver The canonical striver: Julien Sorel in Stendhal’s The Red And The Black A striver is...

In the 1800s horses supplied roughly half of all mechanical labor in the US1. Horses let farmers work ten times more farmland, hauled transit cars, freight, and mail. In the 1880s, a quarter of US cropland grew oats and hay to feed the nation’s biological engines. By 1920 there were...

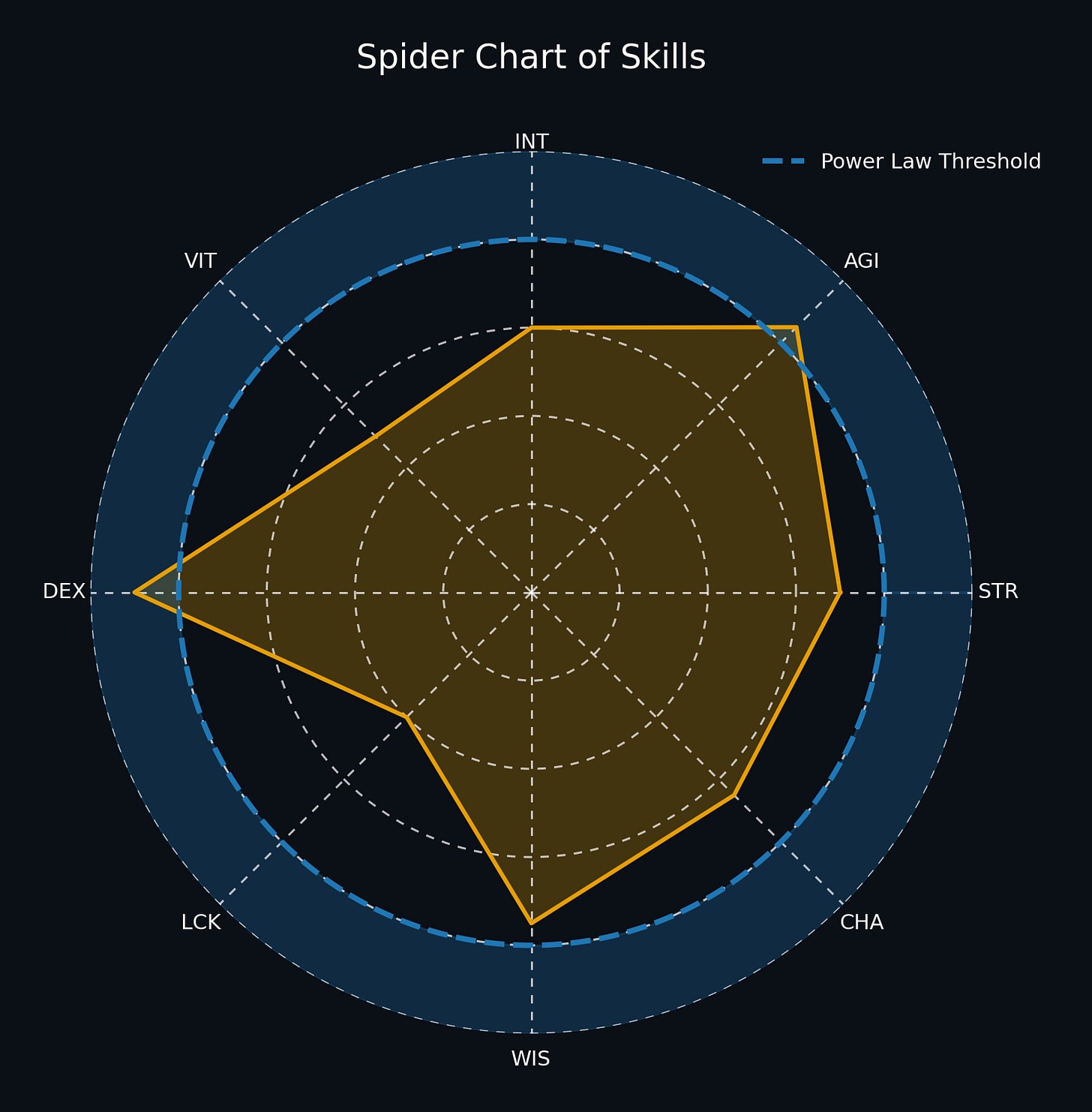
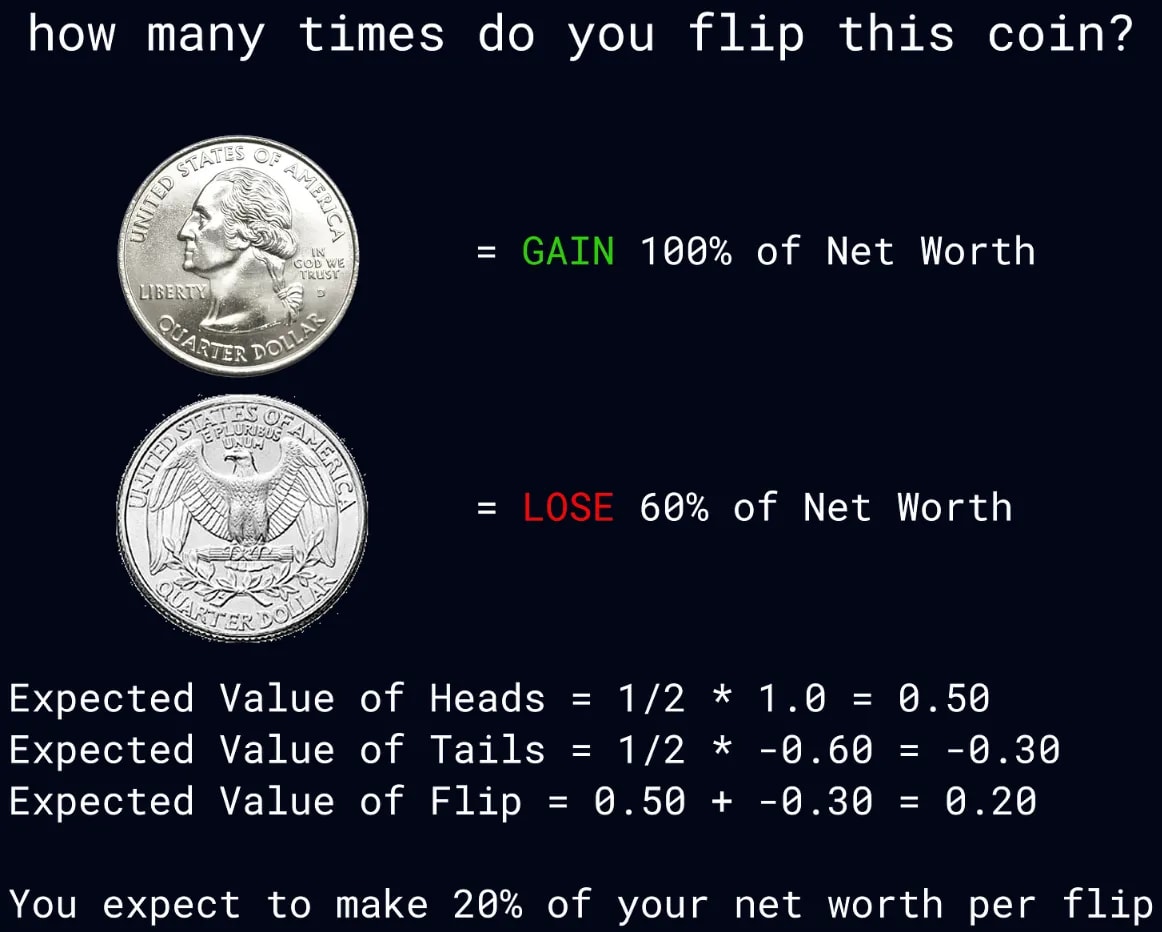
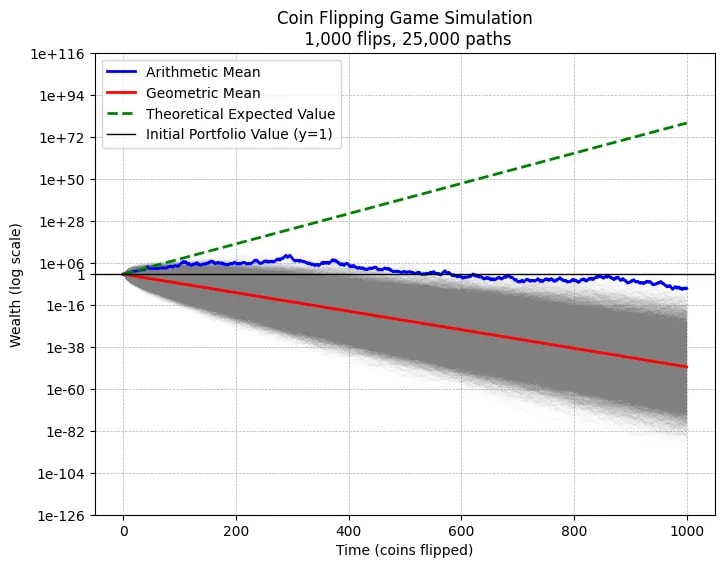
This essay is about shifts in risk taking towards the worship of jackpots and its broader societal implications. Imagine you are presented with this coin flip game. How many times do you flip it? At first glance the game feels like a money printer. The coin flip has positive expected...

crossposted from my blog There are two ways we miscalibrate risk. 1. We risk too much on things that are low conviction 2. We risk too little on things that are high conviction I learned these lessons in poker and in trading and they have helped me reason about broader...

crossposted from substack > It’s tough to get out of bed to do roadwork at 5am when you’ve been sleeping in silk pajamas. > > > —Marvin Hagler I’ve been coasting for the past four months. It’s probably been my first extended break in over six years of grinding. My...

After college I worked for a high frequency trading firm where the basic unit of time was the microsecond. A single blink—about 250,000 µs—was long enough for our algorithms to open and close thousands of positions, each trade born and buried long before a human observer would have even noticed...