Interesting.

If you're stating that generic intelligence was not likely simulated, but generic intelligence in our situation was likely simulated...

Doesn't that fall afoul of the mediocrity principle applied to generic intelligence overall?

(As an aside, this does somewhat conflate 'intelligence' and 'computation'; I am assuming that intelligence requires at least some non-zero amount of computation. It's good to make this assumption explicit I suppose.)

I should probably reread the paper.

That being said:

No, it doesn't, any more than "Godel's theorem" or "Turing's proof" proves simulations are impossible or "problems are NP-hard and so AGI is impossible".

I don't follow your logic here, which probably means I'm missing something. I agree that your latter cases are invalid logic. I don't see why that's relevant.

simulators can simply approximate

This does not evade this argument. If nested simulations successively approximate, total computation decreases exponentially (or the Margolus–Levitin theorem doesn't apply everywhere).

simulate smaller sections

This does not evade this argument. If nested simulations successively simulate smaller sections, total computation decreases exponentially (or the Margolus–Levitin theorem doesn't apply everywhere).

tamper with observers inside the simulation

This does not evade this argument. If nested simulations successively tamper with observers, this does not affect total computation - total computation still decreases exponentially (or the Margolus–Levitin theorem doesn't apply everywhere).

slow down the simulation

This does not evade this argument. If nested simulations successively slow down, total computation^[1] decreases exponentially (or the Margolus–Levitin theorem doesn't apply everywhere).

cache results like HashLife

This does not evade this argument. Using HashLife, total computation still decreases exponentially (or the Margolus–Levitin theorem doesn't apply everywhere).

(How do we simulate anything already...?)

By accepting a multiplicative slowdown per level of simulation in the infinite limit^[2], and not infinitely nesting.

1. ^{^}

   See note 2 in the parent: "Note: I'm using 'amount of computation' as shorthand for 'operations / second / Joule'. This is a little bit different than normal, but meh."

2. ^{^}

   You absolutely can, in certain cases, get no slowdown or even a speedup by doing a finite number of levels of simulation. However, this does not work in the limit.

Said argument applies if we cannot recursively self-simulate, regardless of reason (Margolus–Levitin theorem, parent turning the simulation off or resetting it before we could, etc).

In order for 'almost all' computation to be simulated, most simulations have to be recursively self-simulating. So either we can recursively self-simulate (which would be interesting), we're rare (which would also be interesting), or we have a non-zero chance we're in the 'real' universe.

Interesting.

I am also skeptical of the simulation argument, but for different reasons.

My main issue is: the normal simulation argument requires violating the Margolus–Levitin theorem^[1], as it requires that you can do an arbitrary amount of computation^[2] via recursively simulating^[3].

This either means that the Margolus–Levitin theorem is false in our universe (which would be interesting), we're a 'leaf' simulation where the Margolus–Levitin theorem holds, but there's many universes where it does not (which would also be interesting), or we have a non-zero chance of not being in a simulation.

This is essentially a justification for 'almost exactly all such civilizations don't go on to build many simulations'.

1. ^{^}

   A fundamental limit on computation: $\le 6\ast {10}^{33}\text{operations}/\text{second}/\text{Joule}$

2. ^{^}

   Note: I'm using 'amount of computation' as shorthand for 'operations / second / Joule'. This is a little bit different than normal, but meh.

3. ^{^}

   Call the scaling factor - of amount of computation necessary to simulate X amount of computation - $C$. So e.g. $C=0.5$ means that to simulate 1 unit of computation you need 2 units of computation. If $C\ge 1$, then you can violate the Margolus–Levitin theorem simply by recursively sub-simulating far enough. If $C<1$, then a universe that can do $X$ computation can simulate no more than $CX$ total computation regardless of how deep the tree is, in which case there's at least a $1-C$ chance that we're in the 'real' universe.

Playing less wouldn’t decrease my score

Interesting. Is this typically the case with chess? Humans tend to do better with tasks when they are repeated more frequently, albeit with strongly diminishing returns.

being distracted is one of the effects of stress.

Absolutely, which makes it very difficult to tease apart 'being distracted as a result of stress caused by X causing a drop' and 'being distracted due to X causing a drop'.

solar+batteries are dropping exponentially in price

Pulling the data from this chart from your source:

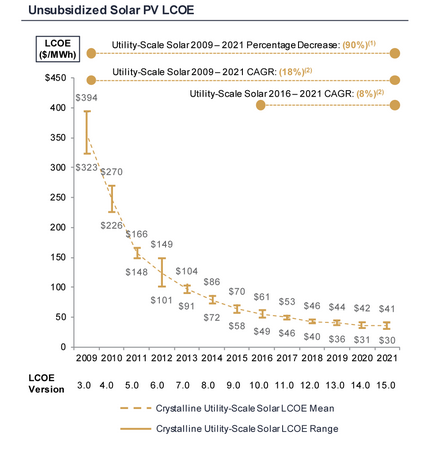
...and fitting^[1] an exponential trend with offset^[2], I get:

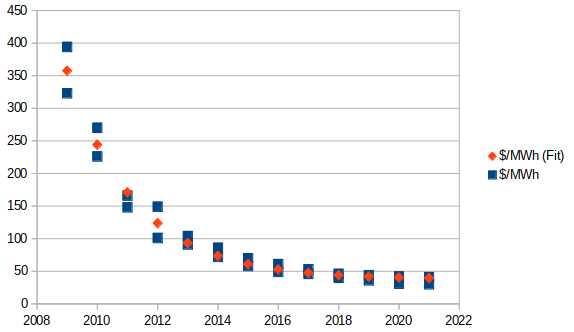
(Pardon the very rough chart.)

This appears to be a fairly good fit^[3], and results in the following trend/formula:

$\$/MWh=319.67\ast e^{-0.43796\ast (\text{year}-2009)}+37.706$^[4]

This is an exponentially-decreasing trend... but towards a decidedly positive horizontal asymptote.

This essentially indicates that we will get minimal future scaling, if any. $37.71/MWh is already within the given range.

For reference, here's what the best fit looks like if you try to force a zero asymptote:

$\$/MWh=336.02\ast e^{-0.28833\ast (\text{year}-2009)}$

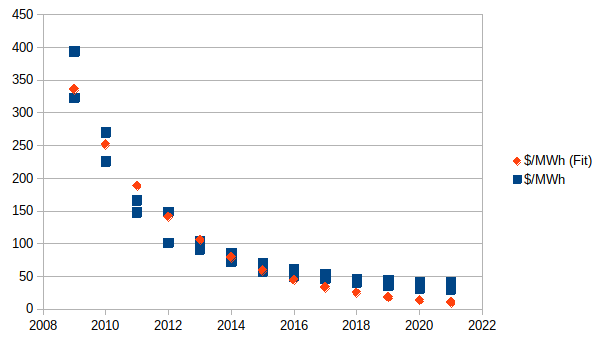
This is fairly obviously a significantly worse fit^[5].

Why do you believe that solar has an asymptote towards zero cost?^[6]

fossils usually don't need storage

Absolutely, which is one of the reasons why in the absence of wanting clean energy people tend to lean towards fossil fuels.

1. ^{^}

   Nonlinear least squares.

2. ^{^}

   I'm treating the high and low as two different data points for each year, which isn't quite right, but meh.

3. ^{^}

   Admittedly, just from eyeballing it.

4. ^{^}

   Yes, this could be simplified. That being said, I get numerical stability issues if I don't include the year offset; it's easier to just include said offset.

5. ^{^}

   Admittedly, this is a 2-parameter fit not a 3-parameter fit; I don't know offhand of a good alternative third parameter to add to the fit to make it more of an apples-to-apples comparison.

6. ^{^}

   As an aside, people fitting exponential trends without including an offset term and then naively extrapolating, when exponential trends with offset terms fit significantly better and don't result in absurd conclusions, is a bit of a pet peeve of mine.

Too bad. My suspects for confounders for that sort of thing would be 'you played less at the start/end of term' or 'you were more distracted at the start/end of term'.

First, nuclear power is expensive compared to the cheapest forms of renewable energy and is even outcompeted by other “conventional” generation sources [...] The consequence of the current price tag of nuclear power is that in competitive electricity markets it often just can’t compete with cheaper forms of generation.

[snip chart]

Source: Lazard

This estimate does not seem to include capacity factors or cost of required energy storage, assuming I read it correctly. Do you have an estimate that does?

Thirdly, nuclear power gives you energy independence. This became very clear during Russia’s invasion of Ukraine. France, for example, had much fewer problems cutting ties with Russia than e.g. Germany. While countries might still have to import Uranium, the global supplies are distributed more evenly than with fossil fuels, thereby decreasing geopolitical relevance. Uranium can be found nearly everywhere.

Also, you can extract uranium from seawater. This has its own problems, and is still more expensive than mines currently. However, this puts a cap on the cost of uranium for any (non-landlocked) country, which is a very good thing for contingency purposes.

(Also, there are silly amounts of uranium in seawater. 35 million tons of land-based reserves, and 4.6 billion in seawater. At very low concentrations, but still.)

How much did you play during the start / end of term compared to normal?