victorsintnicolaas

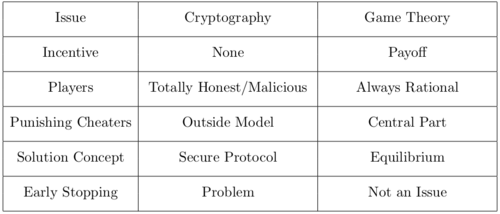
Crossposted from: Equilibria Club It's time for a puzzle involving two fields: game theory and cryptography! Both fields model self-interested agents in a competitive setting. In game theory, we list actions and payoffs, after which we can determine which actions will benefit agents the most. In cryptography, we model actions to ensure agents only get a limited amount of information. Comparison of concepts between cryptography and game theory The problem: game of chicken To illustrate how cryptography can be used to achieve better outcomes in a game, we're going to look at the "Game of Chicken". Imagine two players driving towards each other in a car, in principle wanting to avoid a collision, but also not wanting to chicken out. The standard two-player game is characterized by the following payoffs: Player 1 cooperatesPlayer 1 defectsPlayer 2 cooperates(4, 4)(1, 5)Player 2 defects(5, 1)(0, 0) > "While the “wisest” pair of actions is (C, C), this is not a Nash equilibrium, since both players are willing to deviate (believing that the other player will stay at C)." We can display the three Nash equilibria (the optimal actions for non-coordinating self-interested players) on a graph. The players will either (cooperate, defect), (defect, cooperate), or have a 50% chance of (cooperate, defect) and (defect, cooperate). Three Nash equilibria in the extended game In the previous post about game theory, I referred to the Folk Theorem of game theory, which says that many equilibria can be enforced by the players in iterated games. However, those enforceable equilibria all fall in the so-called convex hull of the Nash equilibria - which is any situation contained by the Nash equilibria. In the Game of Chicken, situations in the convex hull are all situations below the purple diagonal, leading to a maximum total payoff of 6. Is there any way we can do better? Well yes! We can try to a