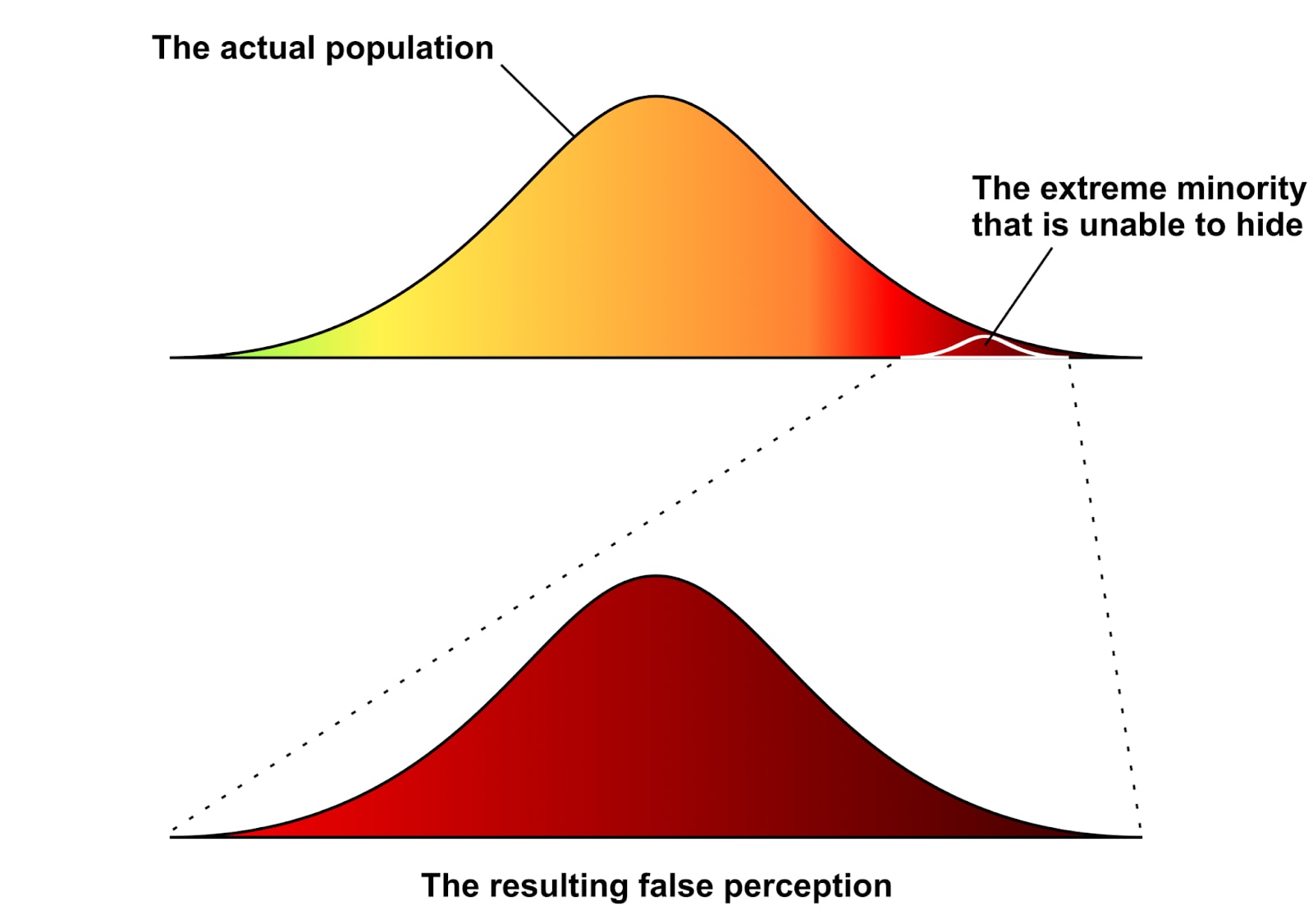
Mostly unrelated to the content of the post, but looking at the distributions in this image
this reminds me quite a lot of the anecdote about a Poincaré and the baker.
The anecdote goes:
"[...] Poincaré, who made a habit of picking up a loaf of bread each day, noticed after weighing his loaves that they averaged about 950 grams instead of the 1000 grams advertised. He complained to the authorities and afterwards received bigger loaves. Still he had a hunch that something about his bread wasn't kosher. And so with the patience only a famous --- or at least tenured --- scholar can afford, he carefully weighed his bread every day for the next year. Though his bread now averaged closer to 1000 grams, if the baker had been honestly handing him random loaves the number of loaves heavier and lighter than the mean should [...] have diminished following the bell shaped pattern of the error law. Instead, Poincaré found that there were too few light loaves and a surplus of heavy ones." - The Drunkards Walk pp 155-156, Leonard Mlodinow
Now this anecdote is probably false and the exact distribution of a selection from the tale depends on the exact mechanics of the selection effect. I still find useful when thinking of selections from normal distributions.
If something doesn't look normal then there is probably a dominant factor shaping the distribution (compared to many small which creates the normal shape).
Another hypothesis: Your description of the task is
the hard parts of application pentesting for LLMs, which are 1. Navigating a real repository of code too large to put in context, 2. Inferring a target application's security model, and 3. Understanding its implementation deeply enough to learn where that security model is broken.
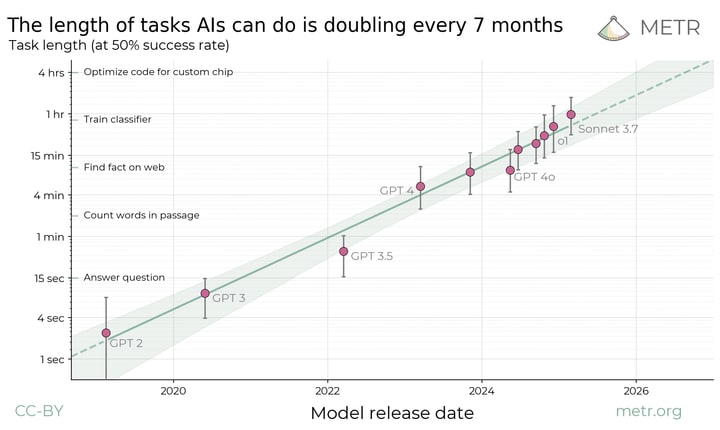
From METR's recent investigation on long tasks you would expect current models not to perform well on this.
I doubt a human professional could do the tasks you describe in something close to an hour, so perhaps its just currently too hard and the current improvements don't make much of a difference for the benchmark, but it might in the future.
(Perhaps you're thinking of this https://www.lesswrong.com/posts/EKu66pFKDHFYPaZ6q/the-hero-with-a-thousand-chances)
Good formulation. "Given it's Monday" can have two different meanings:
- you learn that you will only be awoken on Monday, then it's 50%
- you awake assign 1/3 probability to each instance and then make the update
So it turns out to 50 % for both but it wasn't initially obvious to me that these two ways would have the same result.
The possible observer instances and their probability are:
- Heads 50 %
- Red room 25 %
- Blue room 25 %
- Tails 50 %
- Red room 50 % (On Monday or Tuesday)
- Blue room 50 % (On Monday or Tuesday)
If I choose a strategy "bet only if blue" (or equivalentely "bet only if red") then expected value for this strategy is so I choose to follow this strategy.
I don't remember what halfer and thirder were or what position I consider to be correct.
Capabilities leakages don’t really “increase race dynamics”.
Do people actually claim this? Shorter timelines seems like a more reasonable claim to make. To jump directly to impacts on race dynamics is skipping at least one step.
To me it feels like this policy is missing something that accounts for a big chunk of the risk.
While recursive self-improvement is covered by the "Autonomy and replication" point, there is another risk from actors that don't intentionally cause large scale harm but use your system to make improvements to their own systems as they don't follow your RSP. This type of recursive improvement doesn't seem to be covered by any of "Misuse" or "Autonomy and replication".
In short it's about risks due to shortening of timelines.
You can see twin birth rates fell sharply in the late 90s
Shouldn't this be triplet birthrates? Twin birthrates look pretty stable in comparison.
These april fools posts are dangerous off-season. With my experience of LessWrong this read as on the tail end of what someone would do, rather than out-of-distribution.