Impact of " 'Let's think step by step' is all you need"?
Title from: https://twitter.com/arankomatsuzaki/status/1529278581884432385. This is not quite a linkpost for this paper. Nonetheless, the abstract is: > Pretrained large language models (LLMs) are widely used in many sub-fields of natural language processing (NLP) and generally known as excellent few-shot learners with task-specific exemplars. Notably, chain of thought (CoT) prompting, a recent technique for eliciting complex multi-step reasoning through step-by-step answer examples, achieved the state-of-the-art performances in arithmetics and symbolic reasoning, difficult system-2 tasks that do not follow the standard scaling laws for LLMs. While these successes are often attributed to LLMs' ability for few-shot learning, we show that LLMs are decent zero-shot reasoners by simply adding ``Let's think step by step'' before each answer. Experimental results demonstrate that our Zero-shot-CoT, using the same single prompt template, significantly outperforms zero-shot LLM performances on diverse benchmark reasoning tasks including arithmetics (MultiArith, GSM8K, AQUA-RAT, SVAMP), symbolic reasoning (Last Letter, Coin Flip), and other logical reasoning tasks (Date Understanding, Tracking Shuffled Objects), without any hand-crafted few-shot examples, e.g. increasing the accuracy on MultiArith from 17.7% to 78.7% and GSM8K from 10.4% to 40.7% with an off-the-shelf 175B parameter model. The versatility of this single prompt across very diverse reasoning tasks hints at untapped and understudied fundamental zero-shot capabilities of LLMs, suggesting high-level, multi-task broad cognitive capabilities may be extracted through simple prompting. We hope our work not only serves as the minimal strongest zero-shot baseline for the challenging reasoning benchmarks, but also highlights the importance of carefully exploring and analyzing the enormous zero-shot knowledge hidden inside LLMs before crafting finetuning datasets or few-shot exemplars. Consider the following image, t
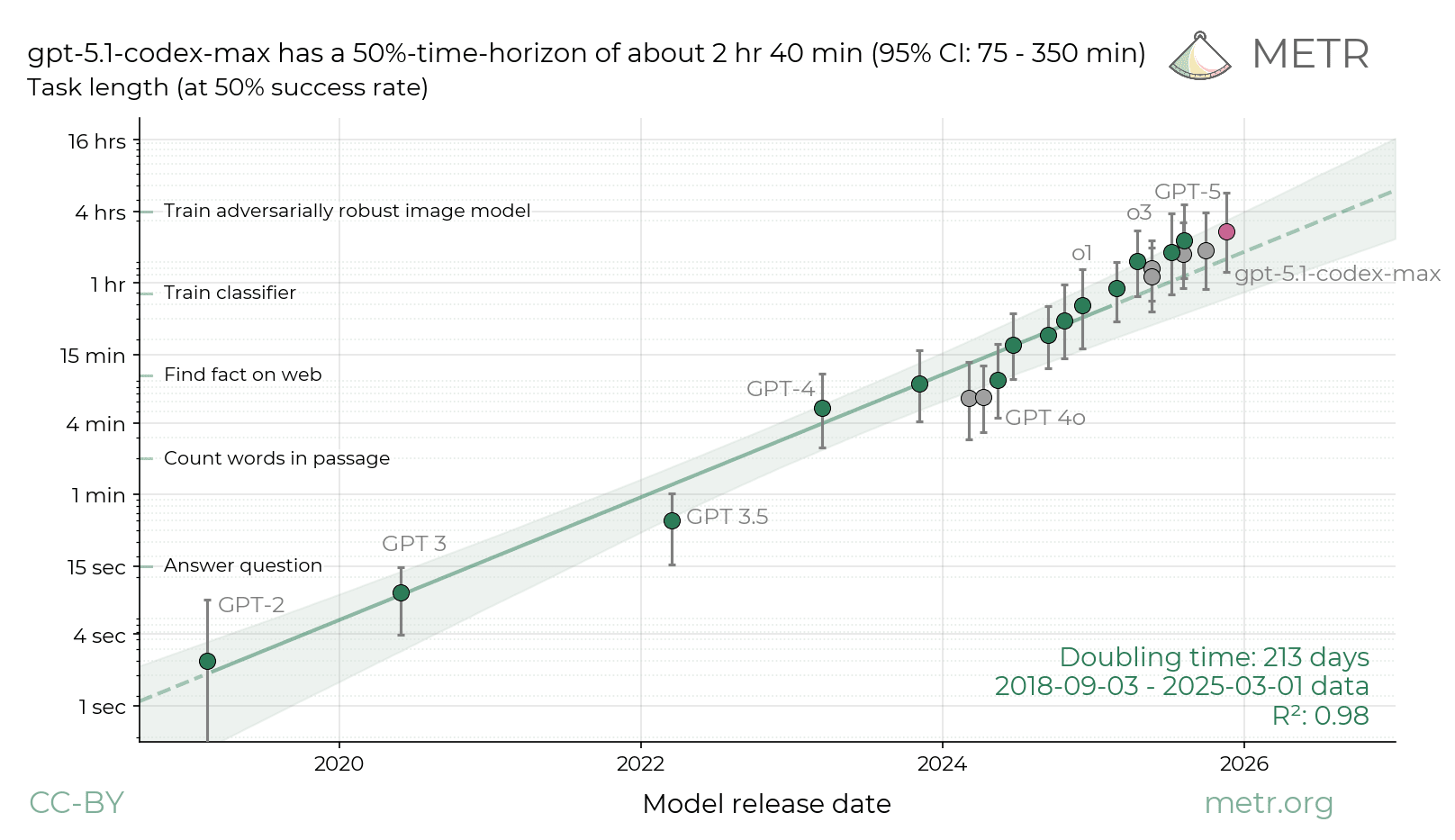
Gpt5.2 did in fact buck the trend from the previous graph. (The grey line on t is graph is the old trend line.)
Together with opus 4.5, gpt5.2 caused metr to enrich their task base, and changed doubling time on the graph from 213 or 212 days to 128 days.
The same logic as above suggests a regression to the mean regarding the next release: it should make doubling time go down a little. This is only if time horizons continue to be a reasonable measure of capability, which I doubt, as argued here.
Thank you Baybar for asking me to be specific. I should have been even more specific.