An associative operation is a binary operation such that for all in , . For example, is an associative function, because for all values of and . When an associative function is used to combine many elements in a row, parenthesis can be dropped, because the order of application is irrelevant.
Imagine that you're trying to use to combine 3 elements and into one element, via two applications of . is associative if i.e., if the result is the same regardless of whether you apply to and first (and then apply that result to ), or whether you apply to and first (and then apply to that result).
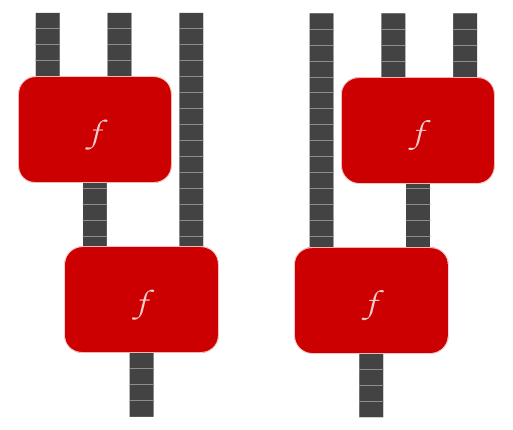
Visualizing as a physical mechanism, there are two different ways to hook up two copies of together to create a function which takes three inputs and produces one output:
An associative function is one where the result is the same no matter which way the functions are hooked up, which means that the result of using twice to turn three inputs into one output yields the same output regardless of the order in which we combine adjacent inputs.
By similar argument, an associative operator also gives rise (unambiguously) to functions meaning that associative functions can be seen as a family of functions on lists.
This justifies the omission of parenthesis when writing expressions where an associative operator is applied to many inputs in turn, because the order of application does not matter. For example, multiplication is associative, so we can write expressions such as without ambiguity. It makes no difference whether we compute the result by first multiplying 2 by 3, or 3 by 4, or 4 by 5.
By contrast, the function prependx that sticks its inputs together and puts an x on the front is not associative: prependx(prependx("a","b"),"c") = "xxabc", but prependx("a",prependx("b","c"))=xaxbc.