Bayes' rule: Functional form

Bayes' rule generalizes to continuous functions, and states, "The posterior probability density is proportional to the likelihood function times the prior probability density."

Example

Suppose we have a biased coin with an unknown bias $b$ between 0 and 1 of coming up heads on each individual coinflip. Since the bias $b$ is a continuous variable, we express our beliefs about the coin's bias using a probability density function $P (b),$ where $P (b) \cdot d b$ is the probability that $b$ is in the interval $[b + d b]$ for $d b$ small. (Specifically, the probability that $b$ is in the interval $[a, b]$ is $\int_{a}^{b} P (b) d b .$ )

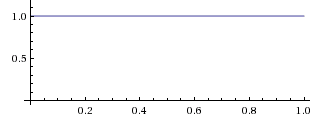
By hypothesis, we start out completely ignorant of the bias $b,$ meaning that all initial values for $b$ are equally likely. Thus, $P (b) = 1$ for all values of $b,$ which means that $P (b) d b = d b$ (e.g., the chance of $b$ being found in the interval from 0.72 to 0.76 is 0.04).

plot y = 1 + x * 0, x = 0 to 1

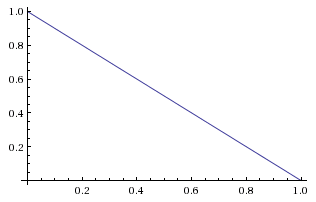
We then flip the coin, and observe it to come up tails. This is our first piece of evidence. The likelihood $L_{t_{1}} (b)$ of observation $t_{1}$ given bias $b$ is a continuous function of $b$ , equal to 0.4 if $b = 0.6,$ 0.67 if $b = 0.33,$ and so on (because $b$ is the probability of heads and the observation was tails).

Graphing the likelihood function $L_{t_{1}} (b)$ as it takes in the fixed evidence $t_{1}$ and ranges over variable $b,$ we obtain the straightforward graph $L_{t_{1}} (b) = 1 - b .$

plot y = 1 - x, x = 0 to 1

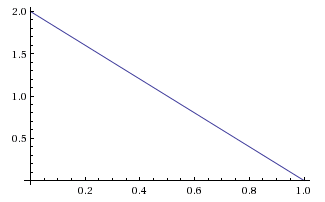
If we multiply the likelihood function by the prior probability function as it ranges over $b$ , we obtain a relative probability function on the posterior, $O (b ∣ t_{1}) = L_{t_{1}} (b) \cdot P (b) = 1 - b,$ which gives us the same graph again:

plot y = 1 - x, x = 0 to 1

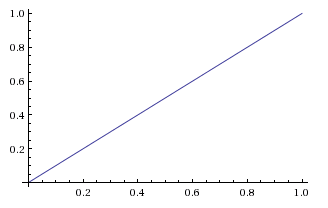
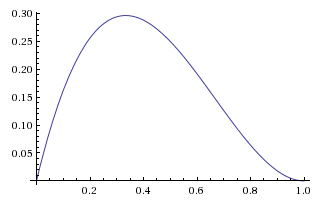
But this can't be our posterior probability function because it doesn't integrate to 1. $\int_{0}^{1} (1 - b) d b = \frac{1}{2} .$ (The area under a triangle is half the base times the height.) Normalizing this relative probability function will give us the posterior probability function:

$P (b ∣ t_{1}) = \frac{O (b ∣ t_{1})}{\int_{0}^{1} O (b ∣ t_{1}) d b} = 2 \cdot (1 - f)$

plot y = 2(1 - x), x = 0 to 1

The shapes are the same, and only the y-axis labels have changed to reflect the different heights of the pre-normalized and normalized function

Regraph these graphs with actual height changes

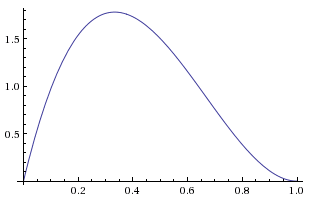
Suppose we now flip the coin another two times, and it comes up heads then tails. We'll denote this piece of evidence $h_{2} t_{3} .$ Although these two coin tosses pull our beliefs about $b$ in opposite directions, they don't cancel out — far from it! In fact, one value of $b$ ("the coin is always tails") is completely eliminated by this evidence, and many extreme values of $b$ ("almost always heads" and "almost always tails") are hit badly. That is, while the heads and the coins tails pull our beliefs in opposite directions, they don't pull with the same strength on all possible values of $b .$

We multiply the old belief

plot y = 2(1 - x), x = 0 to 1

by the additional pieces of evidence

and

and obtain the posterior relative density

plot y = 2(1 - x)x(1 - x), x = 0 to 1

which is proportional to the normalized posterior probability

plot y = 12(1 - x)x(1 - x), x = 0 to 1

Writing out the whole operation from scratch:

$P (b ∣ t_{1} h_{2} t_{3}) = \frac{L_{t_{1} h_{2} t_{3}} (b) \cdot P (b)}{P (t_{1} h_{2} t_{3})} = \frac{(1 - b) \cdot b \cdot (1 - b) \cdot 1}{\int_{0}^{1} (1 - b) \cdot b \cdot (1 - b) \cdot 1 d b} = 12 \cdot b (1 - b)^{2}$

Note that it's okay for a posterior probability density to be greater than 1, so long as the total probability mass isn't greater than 1. If there's probability density 1.2 over an interval of 0.1, that's only a probability of 0.12 for the true value to be found in that interval.

Thus, intuitively, Bayes' rule "just works" when calculating the posterior probability density from the prior probability density function and the (continuous) likelihood ratio function. A proof is beyond the scope of this guide; refer to Proof of Bayes' rule in the continuous case.