Odds form

Bayes's Rule (in the odds form or proportional form) states:

$\frac{P\left(H_i\right)}{P\left(H_j\right)}\times \frac{P\left(e|H_i\right)}{P\left(e|H_j\right)}=\frac{P\left(H_i|e\right)}{P\left(H_j|e\right)}$

Interpreting $H$ as the hypotheses under consideration, $e$ as the evidence being observed, and giving "prior odds", "likelihood ratio", and "posterior odds" their standard meanings, Bayes's Rule states:

$\text{Prior odds}\times \text{Likelihood ratio}=\text{Posterior odds}$

To prove Bayes's Rule, use the definition of conditional probability:

$P\left(X|Y\right)=\frac{P(X\wedge Y)}{P\left(Y\right)}$

As follows:

$\frac{P\left(H_i\right)}{P\left(H_j\right)}\times \frac{P\left(e|H_i\right)}{P\left(e|H_j\right)}=\frac{P(e\wedge H_i)}{P(e\wedge H_j)}=\frac{P(e\wedge H_i)/P\left(e\right)}{P(e\wedge H_j)/P\left(e\right)}=\frac{P\left(H_i|e\right)}{P\left(H_j|e\right)}$

Example

For a specific example, consider the problem:

20% of the patients in the screening population start out with Diseasitis. Among patients with Diseasitis, 90% turn the tongue depressor black. 30% of the patients without Diseasitis will also turn the tongue depressor black. Among all the patients with black tongue depressors, how many have Diseasitis?

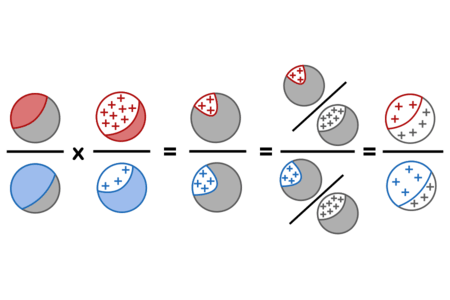
Bayes's Rule would license solving the problem by saying, "The prior odds of Diseasitis vs. health are 1 : 4, the likelihood ratio for positive results is 3 : 1 for sick vs. healthy patients, therefore the posterior odds are 3 : 4, corresponding to a probability of 3/7 that a patient with a positive test result hase Diseasitis."

This reasoning would be valid because:

$\begin{array}{c} \dfrac{\mathbb P(sick)}{\mathbb P(\neg sick)} \times \dfrac{\mathbb P(positive|sick)}{\mathbb P(positive|\neg sick)} \0.3em = \dfrac{\mathbb P(positive \wedge sick)}{\mathbb P(positive \wedge \neg sick)} \0.3em = \dfrac{\mathbb P(positive \wedge sick) / \mathbb P(positive)}{\mathbb P(positive \wedge \neg sick) / \mathbb P(positive)} \0.3em = \dfrac{\mathbb P(sick|positive)}{\mathbb P(\neg sick|positive)} \end{array} $

The quantities corresponding to the steps above would be as follows:

$\frac{20\%}{80\%}\times \frac{90\%}{30\%}=\frac{18\%}{24\%}=\frac{0.18/0.42}{0.24/0.42}=\frac{43\%}{57\%}$

Or in a visual interpretation:

Probability form

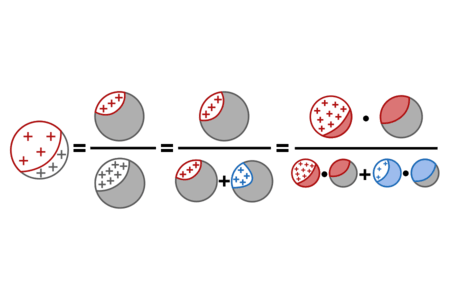
As a formula for a single conditional probability $P\left(H_i|e\right),$ with the variable $H$ having states $H_k$ that are mutually exclusive and exhaustive, Bayes's Theorem states:

$P\left(H_i|e\right)=\frac{P\left(e|H_i\right)\cdot P\left(H_i\right)}{{\sum }_{k}P\left(e|H_k\right)\cdot P\left(H_k\right)}$

This follows from the definition of conditional probability:

$P\left(H_i|e\right)=\frac{P(e\wedge H_i)}{P\left(e\right)})=\frac{P\left(e|H_i\right)\cdot P\left(H_i\right)}{P\left(e\right)}$

From the law of marginal probability:

$P\left(e\right)={\sum }_{k}P(e\wedge H_k)$

And from the definition of conditional probability:

$P(e\wedge H_k)=P\left(e|H_k\right)\cdot P\left(H_k\right)$

Using the Diseasitis example above, this would say:

$$$\begin{array}{c}P\left(sick|positive\right)=\frac{P(positive\wedge sick)}{P\left(positive\right)}=\frac{P(positive\wedge sick)}{P(positive\wedge sick)+P(positive\wedge \neg sick)}=\frac{P\left(positive|sick\right)\cdot P\left(sick\right)}{\left(P\right(positive|sick)\cdot P(sick\left)\right)+\left(P\right(positive|\neg sick)\cdot P(\neg sick\left)\right)}\end{array}$$ $

Using the specific numbers:

$3/7=\frac{0.18}{0.42}=\frac{0.18}{0.18+0.24}=\frac{90\%\ast 20\%}{(90\%\ast 20\%)+(30\%\ast 80\%)}$