Odds form

Bayes's Rule (in the odds form or proportional form) states:

$$\frac{P\left(H_i\right)}{P\left(H_j\right)}\times \frac{P(e\mid H_i)}{P(e\mid H_j)}=\frac{P(H_i\mid e)}{P(H_j\mid e)}$$

Interpreting $H$ as the hypotheses under consideration, $e$ as the evidence being observed, and giving "prior odds", "likelihood ratio", and "posterior odds" their standard meanings, Bayes's Rule states:

$$\text{Prior odds}\times \text{Likelihood ratio}=\text{Posterior odds}$$

To prove Bayes's Rule, use the definition of conditional probability:

$$P(X\mid Y)=\frac{P(X\wedge Y)}{P\left(Y\right)}$$

As follows:

$$\frac{P\left(H_i\right)}{P\left(H_j\right)}\times \frac{P(e\mid H_i)}{P(e\mid H_j)}=\frac{P(e\wedge H_i)}{P(e\wedge H_j)}=\frac{P(e\wedge H_i)/P\left(e\right)}{P(e\wedge H_j)/P\left(e\right)}=\frac{P(H_i\mid e)}{P(H_j\mid e)}$$

Example

For a specific example, consider the problem:

20% of the patients in the screening population start out with Diseasitis. Among patients with Diseasitis, 90% turn the tongue depressor black. 30% of the patients without Diseasitis will also turn the tongue depressor black. A patient turns a tongue depressor black. Given only this information, what is the probability that they have Diseasitis?

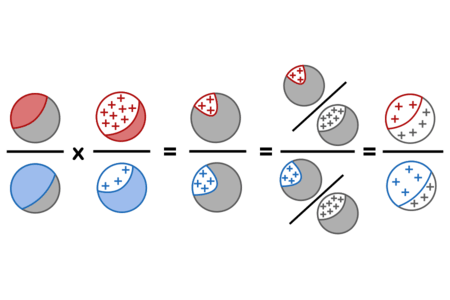
Bayes' solves the problem by saying, "The prior odds of Diseasitis vs. health are 1 : 4, the likelihood ratio for positive results is 3 : 1 for sick vs. healthy patients, therefore the posterior odds are 3 : 4, corresponding to a probability of 3/7 that a patient with a positive test result hase Diseasitis."

This reasoning would be valid because:

$$\begin{array}{c}\frac{P\left(sick\right)}{P\left(\neg sick\right)}\times \frac{P(positive\mid sick)}{P(positive\mid \neg sick)}\\ =\frac{P(positive\wedge sick)}{P(positive\wedge \neg sick)}\\ =\frac{P(positive\wedge sick)/P\left(positive\right)}{P(positive\wedge \neg sick)/P\left(positive\right)}\\ =\frac{P(sick\mid positive)}{P(\neg sick\mid positive)}\end{array}$$

The quantities corresponding to the steps above would be as follows:

$$\frac{20\%}{80\%}\times \frac{90\%}{30\%}=\frac{18\%}{24\%}=\frac{0.18/0.42}{0.24/0.42}=\frac{43\%}{57\%}$$

Or in a visual interpretation:

Probability form

As a formula for a single conditional probability $P(H_i\mid e),$ with the variable $H$ having states $H_k$ that are mutually exclusive and exhaustive, Bayes's Theorem states:

$$P(H_i\mid e)=\frac{P(e\mid H_i)\cdot P\left(H_i\right)}{{\sum }_{k}P(e\mid H_k)\cdot P\left(H_k\right)}$$

This follows from the definition of conditional probability:

$$P(H_i\mid e)=\frac{P(e\wedge H_i)}{P\left(e\right)})=\frac{P(e\mid H_i)\cdot P\left(H_i\right)}{P\left(e\right)}$$

From the law of marginal probability:

$$P\left(e\right)=\sum _{k}P(e\wedge H_k)$$

And from the definition of conditional probability:

$$P(e\wedge H_k)=P(e\mid H_k)\cdot P\left(H_k\right)$$

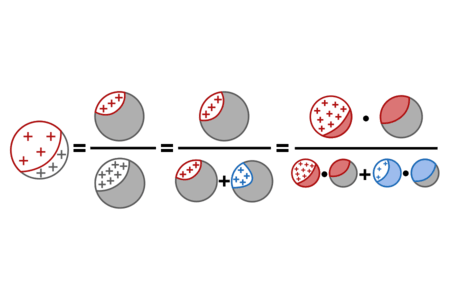
Using the Diseasitis example above, this would say:

$$\begin{array}{c}P(sick\mid positive)=\frac{P(positive\wedge sick)}{P\left(positive\right)}\\ =\frac{P(positive\wedge sick)}{P(positive\wedge sick)+P(positive\wedge \neg sick)}\\ =\frac{P(positive\mid sick)\cdot P\left(sick\right)}{\left(P\right(positive\mid sick)\cdot P(sick\left)\right)+\left(P\right(positive\mid \neg sick)\cdot P(\neg sick\left)\right)}\end{array}$$

Using the specific numbers:

$$3/7=\frac{0.18}{0.42}=\frac{0.18}{0.18+0.24}=\frac{90\%\ast 20\%}{(90\%\ast 20\%)+(30\%\ast 80\%)}$$

Visually: