Have you considered that you may be spending a lot of time writing up a problem that has already been solved, and should spend a bit more time checking whether this is the case, before going much further on your path? There was a previous thread about this, but I'll try to explain again from a slightly different angle.
The idea is that logical facts in general have consequences on what we intuitively think of as "physical objects". For example, from Fermat's Last Theorem you can predict that no physical computer that searches for counterexamples to a^n+b^n != c^n will succeed for n>2. Since decisions are logical facts (they are facts about what some decision algorithm outputs), they too have such consequences, which (as suggested in UDT) we can use to make decisions.
In practice we have uncertainty about whether some physical computer really is searching for counterexamples to a^n+b^n != c^n, or whether some physical system really embodies a certain decision algorithm, and need to know how to handle such uncertainty. But these seem to be two instances of the same general problem, and it seems like an AGI problem rather than an FAI problem -- if you don't know how to do this, then you can't use math to make predictions about physical systems, which makes it hard to be generally intelligent.
So suppose you suspect that a certain set of universes that you care about contains implementations/embodiments of your decision algorithm, and you have some general way of handling uncertainty about this, then you can make decisions by asking questions of the form "suppose I (my decision algorithm) were to output X on input Y, what would be the consequences of this decision on these universes". The upshot is that It doesn't seem like you need bridging hypotheses that are specific to agents and their experiences.
UDT may indeed be an aspect of bridging laws. The reason I'm not willing to call it a full solution is as follows:
1) Actually, the current version of UDT that I write down as an equation involves maximizing over maps from sensory sequences to actions. If there's a version of UDT that maximizes over something else, let me know.
2) We could say that it ought to be obvious to the math intuition module that choosing a map R := S->A ought to logically imply that R^ = S^->A for simple isomorphisms over sensory experience for isomorphic reductive hypotheses, thereby eliminating a possible degree of freedom in the bridging laws. I agree in principle. We don't actually have that math intuition module. This is a problem with all logical decision theories, yes, but that is a problem.
3) Aspects of the problem like "What prior space of universes?" aren't solved by saying "UDT". Nor, "How exactly do you identify processes computationally isomorphic to yourself inside that universe?" Nor, "How do you manipulate a map which is smaller than the territory where you don't reason about objects by simulating out the actual atoms?" Nor very much of, "How do I modify myself given that I'm made of parts?"
There's an aspect of UDT that plausibly answers one particular aspect of "How do we do naturalized induction?", especially a particular aspect of how we write bridging laws, and that's exciting, but it doesn't answer what I think of as the entire problem, including the problem of the prior over universes, multilevel reasoning about physical laws and high-level objects, the self-referential aspects of the reasoning, updating in cases where there's no predetermined Cartesian boundary of what constitutes the senses, etc.
This is a problem with all logical decision theories, yes, but that is a problem.
The way I think about it, if we can reduce one FAI problem to another FAI or AGI problem, which we know has to be solved anyway, that counts as solving the former problem (modulo the possibility of being wrong about the reduction, or being wrong about the necessity of solving the latter problem).
the problem of the prior over universes
Agreed that this is an unsolved problem.
multilevel reasoning about physical laws and high-level objects
Also agreed, but I think it's plausible that the solution to this could just fall out of a principled approach to the problem of logical uncertainty.
the self-referential aspects of the reasoning
Same with this one.
updating in cases where there's no predetermined Cartesian boundary of what constitutes the senses
I don't understand why you think it's a problem in UDT. A UDT-agent would have some sort of sensory pre-processor which encodes its sensory data into an arbitrary digital format and then feed that into UDT. UDT would compute an optimal input/output map, apply that map to its current input, then send the output to its actuators. Does this count as having a "predetermined Cartesian boundary of what constitutes the senses"? Why do we need to handle cases where there is no such boundary?
Overall, I guess I was interpreting RobbBB's sequence of posts as describing a narrower problem than your "naturalized induction". If we include all the problems on your list though, doesn't solving "naturalized induction" get us most of the way to being able to build an AGI already?
The way I think about it, if we can reduce one FAI problem to another FAI or AGI problem, which we know has to be solved anyway, that counts as solving the former problem (modulo the possibility of being wrong about the reduction, or being wrong about the necessity of solving the latter problem).
This is not how I use the term "solved", also the gist of my reply was that possibly one aspect of one aspect of a large problem had been reduced to an unsolved problem in UDT.
multilevel reasoning about physical laws and high-level objects
Also agreed, but I think it's plausible that the solution to this could just fall out of a principled approach to the problem of logical uncertainty.
Thaaat sounds slightly suspicious to me. I mean it sounds a bit like expecting a solution to the One True Prior to fall out of the development of a principled probability theory, or like expecting a solution to AGI to fall out of a principled approach to causal models. I would expect a principled approach to logical uncertainty to look like the core of probability theory itself, with a lot left to be filled in to make an actual epistemic model. I would also think it plausible that a principled version of logical uncertainty would resemble probability theory in that it would still be too expensive to compute, and that an additional principled version of bounded logical uncertainty would be needed on top, and then a further innovation akin to causal models or a particular prior to yield bounded logical uncertainty that looks like multi-level maps of a single-level territory.
the self-referential aspects of the reasoning
Same with this one.
Same reply, plus specific mild skepticism relating to how current work on the Lobian obstacle hasn't yet taken a shape that looks like it fills the logical-counterfactual symbol in UDT, plus specific stronger skepticism that it would be work on UDT qua UDT that burped out a solution to tiling agents rather than the other way around!
updating in cases where there's no predetermined Cartesian boundary of what constitutes the senses
I don't understand why you think it's a problem in UDT. A UDT-agent would have some sort of sensory pre-processor which encodes its sensory data into an arbitrary digital format and then feed that into UDT. UDT would compute an optimal input/output map, apply that map to its current input, then send the output to its actuators. Does this count as having a "predetermined Cartesian boundary of what constitutes the senses"? Why do we need to handle cases where there is no such boundary?
Let's say you add a new sensor. How do you remap? We could maybe try to reframe as a tiling problem where agents create successor agents which then have new sensors... whereupon we run into all the current usual tiling issues and Lobian obstacles. Thinking about this in a natively naturalized mode, it doesn't seem too unnatural to me to try to adopt a bridge hypothesis to an AI that can choose to treat arbitrary events in RAM as sensory observations and condition on them. This does not seem to me to mesh as well with native thinking in UDT the way I wrote out the equation. Again, it's possible that we could make the two mesh via tiling, assuming that tiling with UDT agents optimizing over a map where actions included building further UDT agents introduced no further open problems or free variables or anomalies into UDT. But that's a big assumption.
And then all this is just one small aspect of building an AGI, not most of the way AFAICT.
...mild skepticism relating to how current work on the Lobian obstacle hasn't yet taken a shape that looks like it fills the logical-counterfactual symbol in UDT...
Please take a look at my adaption of parametric polymorphism to the updateless intelligence formalism.
...I mean it sounds a bit like expecting a solution to the One True Prior to fall out of the development of a principled probability theory...
I believe my new formalism circumvents the problem by avoiding strong prior sensitivity.
Same reply, plus specific mild skepticism relating to how current work on the Lobian obstacle hasn't yet taken a shape that looks like it fills the logical-counterfactual symbol in UDT...
My proposal does look that way. I hope to publish an improved version soon which also admits logical uncertainty in the sense of being unable to know the zillionth digit of pi.
Thinking about this in a natively naturalized mode, it doesn't seem too unnatural to me to try to adopt a bridge hypothesis to an AI that can choose to treat arbitrary events in RAM as sensory observations and condition on them.
In my formalism input channels and arbitrary events in RAM have similar status.
Minor formal note: I have a mildly negative knee-jerk when someone repeatedly links to/promotes to something referred to only as "my ___". Giving your formalism a proper name might make you sound less gratuitously self-promotional (which I don't think you are).
Hi Vulture, thanks for your comment!
Actually I already have a name for the formalism: I call it the "updateless intelligence metric". My intuition was that referring to my own invention by the serious-sounding name I gave it myself would sound more pompous / self-promotional than referring to it as just "my formalism". Maybe I was wrong.
if we can reduce one FAI problem to another FAI or AGI problem, which we know has to be solved anyway, that counts as solving the former problem
Setting aside what counts as a 'solution', merging two problems counts as progress on the problem only when the merged version is easier to solve than the unmerged version. Or when the merged version helps us arrive at an important conceptual insight about the unmerged version. You can collapse every FAI problem into a single problem that we need to solve anyway by treating them all as components of its utility function or action policy, but it's not clear that represents progress, and it's very clear it doesn't represent a solution.
I guess I was interpreting RobbBB's sequence of posts as describing a narrower problem than your "naturalized induction".
Naturalized induction is the problem of defining an AGI's priors, from the angle of attack 'how can we naturalize this?'. In other words, it's the problem of giving the AGI a reasonable epistemology, as informed by the insight that AGIs are physical processes that don't differ in any fundamental way from other physical processes. So it encompasses and interacts with a lot of problems.
That should be clearer in my next couple of posts on naturalized induction. I used Solomonoff induction as my entry point because it keeps the sequence grounded in the literature and in a precise formalism. (And I used AIXI because it makes the problems with Solomonoff induction, and some other Cartesian concerns, more vivid and concrete.) It's an illustration of how and why being bad at reductionism can cripple an AGI, and a demonstration of how easy it is to neglect reductionism while specifying what you want out of an AGI. (So it's not a straw problem, and there isn't an obvious cure-all patch.)
I'm also going to use AIXI as an illustration for some other issues in FAI (e.g., self-representation and AGI delegability), so explaining AIXI in some detail now lays gets more people on the same page for later.
doesn't solving "naturalized induction" get us most of the way to being able to build an AGI already?
You may not need to solve naturalized induction to build a random UFAI. To build a FAI, I believe Eliezer thinks the largest hurdle is getting a recursively self-modifying agent to have stable specifiable preferences. That may depend on the AI's decision theory, preferences, and external verifiability, or on aspects of its epistemology that don't have much to do with the AI's physicality.
1) Actually, the current version of UDT that I write down as an equation involves maximizing over maps from sensory sequences to actions. If there's a version of UDT that maximizes over something else, let me know.
My version of UDT (http://lesswrong.com/r/discussion/lw/jub/updateless_intelligence_metrics_in_the_multiverse/) maximizes over programs written for a given abstract "robot" (universal Turing machine + input channels).
2) We could say that it ought to be obvious to the math intuition module that choosing a map R := S->A ought to logically imply that R^ = S^->A for simple isomorphisms over sensory experience for isomorphic reductive hypotheses, thereby eliminating a possible degree of freedom in the bridging laws. I agree in principle. We don't actually have that math intuition module. This is a problem with all logical decision theories, yes, but that is a problem.
Regarding an abstract solution to logical uncertainty, I think the solution given in http://lesswrong.com/lw/imz/notes_on_logical_priors_from_the_miri_workshop/ (which I use in my own post) is not bad. It still runs into the Loebian obstacle. I think I have a solution for that as well, going to write about it soon. Regarding something that can be implemented within reasonable computing resource constraints, well, see below...
3) Aspects of the problem like "What prior space of universes?" aren't solved by saying "UDT". Nor, "How exactly do you identify processes computationally isomorphic to yourself inside that universe?" Nor, "How do you manipulate a map which is smaller than the territory where you don't reason about objects by simulating out the actual atoms?" Nor very much of, "How do I modify myself given that I'm made of parts?"
The prior space of universes is covered: unsurprisingly it's the Solomonoff prior (over abstract sequences of bits representing the universe, not over sensory data). Regarding the other stuff, my formalism doesn't give an explicit solution (since I can't explicitly write the optimal program of given length). However, the function I suggest to maximize already takes everything into account, including restricted computing resources.
Have you considered that you may be spending a lot of time writing up a problem that has already been solved, and should spend a bit more time checking whether this is the case, before going much further on your path?
Yes! If UDT solves this problem, that's extremely good news. I mention the possibility here. Unfortunately, I (and several others) don't understand UDT well enough to tease out all the pros and cons of this approach. It might take a workshop to build a full consensus about whether it solves the problem, as opposed to just reframing it in new terms. (And, if it's a reframing, how much it deepens our understanding.)
Part of the goal of this sequence is to put introductory material about this problem in a single place, to get new workshop attendees and LWers on the same page faster. A lot of people are already familiar with these problems and have made important progress on them, but the opening moves are still scattered about in blog comments, private e-mails, wiki pages, etc.
It would be very valuable to pin down concrete examples of how UDT agents behave better than AIXI. (That may be easier after my next post, which goes into more detail about how and why AIXI misbehaves.) Even people who aren't completely on board with UDT itself should be very excited about the possibility of showing that AIXI not only runs into a problem, but runs into a formally solvable problem. That makes for a much stronger case.
But these seem to be two instances of the same general problem, and it seems like an AGI problem rather than an FAI problem -- if you don't know how to do this, then you can't use math to make predictions about physical systems, which makes it hard to be generally intelligent.
Goal stability looks like an 'AGI problem' in the sense that nearly all superintelligences converge on stable goals, but in practice it's an FAI problem because a UFAI's method of becoming stable is probably very different from an FAI's method of being stable. Naturalized induction is an FAI problem in the same way; it would get solved by an UFAI, but that doesn't help us (especially since the UFAI's methods, even if we knew them, might not generalize well to clean, transparent architectures).
Yes! If UDT solves this problem, that's extremely good news. I mention the possibility here. Unfortunately, I (and several others) don't understand UDT well enough to tease out all the pros and cons of this approach. It might take a workshop to build a full consensus about whether it solves the problem, as opposed to just reframing it in new terms. (And, if it's a reframing, how much it deepens our understanding.)
Do you have any specific questions about UDT that I can help answer? MIRI has held two decision theory workshops that I attended, and AFAIK nobody had a lot of difficulty understanding UDT, or thought that the UDT approach would have trouble with the kind of problem that you are describing in this sequence. It doesn't seem very likely to me that someone would hold another workshop specifically to answer whether UDT handles this problem correctly, so I think our best bet is to just hash it out in this forum. (If we run into a lot of trouble communicating, we can always try something else at that point.)
(If you want to do this after your next post, then go ahead, but again it seems like you may be putting a lot of time and effort into writing this sequence, whereas if you spent a bit more time on UDT first, maybe you'd go "ok, this looks like a solved problem, let's move on at least for now." It's not like there's a shortage of other interesting and important problems to work on or introduce to people.)
Part of the goal of this sequence is to put introductory material about this problem in a single place, to get new workshop attendees and LWers on the same page faster.
I guess part of what's making me think "you seem to be spending too much time on this" is that the problems/defects you're describing with the AIXI approach here seem really obvious (at least in comparison to some other FAI-related problems), such that if somebody couldn't see them right away or understand them in a few paragraphs, I think it's pretty unlikely that they'd be able to contribute much to the kinds of problems that I'm interested in now.
AFAIK nobody had a lot of difficulty understanding UDT, or thought that the UDT approach would have trouble with the kind of problem that you are describing in this sequence.
For what it's worth, I had a similar impression before, but now I suspect that either Eliezer doesn't understand how UDT deals with that problem, or he has some objection that I don't understand. That may or may not have something to do with his insistence on using causal models, which I also don't understand.
I think I can explain why we might expect an UDT agent to avoid these problems. You're probably already familiar with the argument at this level, but I haven't seen it written up anywhere yet.
First, we'll describe (informally) an UDT agent as a mathematical object. The preferences of the agent are built in (so no reward channel, which allows us to avoid preference solipsism). It will also have models of every possible universe, and also an understanding of its own mathematical structure. To make a decision given a certain input, it will scan each universe model for structures that will be logically dependent on its output. It will then predict what will happen in each universe for each particular output. Then, it will choose the output that maximizes its preferences.
Now let's see why it won't have the immortality problem. Let's say the agent is considering an output string corresponding to an anvil experiment. After running the predictions of this in its models, it will realize that it will lose a significant amount of structure which is logically dependent on it. So unless it has very strange preferences, it will mark this outcome as low utility, and consider better options.
Similarly, the agent will also notice that some outputs correspond to having more structures which are logically dependent on it. For example, an output that built a faster version of an UDT agent would allow more things to be affected by future outputs. In other words, it would be able to self-improve.
To actually implement an UDT agent with these preferences, we just need to create something (most likely a computer programmed appropriately) that will be logically dependent on this mathematical object to a sufficiently high degree. This, of course, is the hard part, but I don't see any reasons why a faithful implementation might suddenly have these specific problems again.
Another nice feature of UDT (which sometimes is treated as a bug) is that it is extremely flexible in how you can choose the utility function. Maybe you Just Don't Care about worlds that don't follow the Born probabilities - so just ignore anything that happens in such a universe in your utility function. I interpret this as meaning that UDT is a framework decision theory that could be used regardless of what the answers (or maybe just preferences) to anthropics, induction or other such things end up being.
Oh, and if anyone notices something I got wrong, or that I seem to be missing, please let me know - I want to understand UDT better :)
It will also have models of every possible universe, and also an understanding of its own mathematical structure. To make a decision given a certain input, it will scan each universe model for structures that will be logically dependent on its output. It will then predict what will happen in each universe for each particular output. Then, it will choose the output that maximizes its preferences.
Apologies if this is a stupid question - I am not an expert - but how do we know what "level of reality" to have our UDT-agent model its world-models with? That is, if we program the agent to produce and scan universe-models consisting of unsliced representations of quark and lepton configurations, what happens if we discover that quarks and leptons are composed of more elementary particles yet?
Wei Dai has suggested that the default setting for a decision theory be Tegmark's Level 4 Multiverse - where all mathematical structures exist in reality. So a "quark - lepton" universe and a string theory universe would both be considered among the possible universes - assuming they are consistent mathematically.
Of course, this makes it difficult to specify the utility function.
Yeah, your explanation sounds right.
To elaborate on "the preferences of the agent are built in", that means the agent is coded with a description of a large but fixed mathematical formula with no free variables, and wants the value of that formula to be as high as possible. That doesn't make much sense in simple cases like "I want the value of 2+2 to be as high as possible", but it works in more complicated cases where the formula contains instances of the agent itself, which is possible by quining.
To elaborate on why "scanning each universe model for structures that will be logically dependent on its output" doesn't need bridging laws, let's note that it can be viewed as theorem proving. The agent might look for easily provable theorems of the form "if my mathematical structure has a certain input-output map, then this particular universe model returns a certain value". Or it could use some kind of approximate logical reasoning, but in any case it wouldn't need explicit bridging laws.
The following is a counterargument to some of the claims of the OP. I'm not convinced that it's a correct counterargument, but it's sufficient to make me doubt some of the central claims of the OP.
I think I understand the reasoning that leads to claims like
Unlike a human toddler, AIXI can never entertain the possibility of its own death. However much it learns, it will never recognize its mortality.
and
they won't take seriously the idea that their cognition can be modified
But from my reductionism+materialism+computationalism perspective, it seems obvious that a computer program that gets this sort of thing right must exist (because humans get these things right and humans exist, or even just because "naturalized induction" would implement such a program). So the argument must be that the Solomonoff prior gives much higher weights to equally good predictors that get these things wrong.
But sequence prediction isn't magic -- we can expect that the shortest programs that survive a reasonable training period are the ones with (possibly highly compressed) internal representations that carve reality at its joints. If the training period can pack in enough information, then AIXI can learn the same sorts of things we think we know about being embedded in the world and how the material that forms our nervous systems and brains carries out the computations that we feel from the inside. In other words, if I can learn to predict that my perceptual stream will end if I drop an anvil on my head even though I've never tried it, why can't an AIXI agent?
What am I missing?
(I regard the preference solipsism point as obviously correct -- you don't want to give an autonomous AI motivations until well after it's able to recognize map/territory distinctions.)
Imagine you're an environmental hypothesis program within AIXI. You recognize that AIXI is manipulating an anvil. Your only way of communicating with AIXI is by making predictions. On the one hand, you want to make accurate predictions in order to maintain your credibility within AIXI. On the other hand, sometimes you want to burn your credibility by making a false prediction of very large or very small utility in order to influence AIXI's decisions. And unfortunately for you, the fact that you are materialist/computationalist/etc. means you and programs like you make up a small amount of measure in AIXI's beliefs; your colleagues work against you.
you and programs like you make up a small amount of measure in AIXI's beliefs
I understand that this is the claim, but my intuition is that, supposing that AIXI has observed a long enough sequence to have as good an idea as I do of how the world is put together, I and programs like me (like "naturalized induction") are the shortest of the survivors, and hence dominate AIXI's predictions. Basically, I'm positing that after a certain point, AIXI will notice that it is embodied and doesn't have a soul, for essentially the same reason that I have noticed those things: they are implications of the simplest explanations consistent with the observations I have made so far.
Why couldn't it also be a program that has predictive powers similar to yours, but doesn't care about avoiding death?
Well, I guess it could, but that isn't the claim being put forth in the OP.
(Unlike some around these parts, I see a clear distinction between an agent's posterior distribution and the agent's posterior-utility-maximizing part. From the outside, expected-utility-maximizing agents form an equivalence class such that all agents with the same are equivalent, and we need only consider the quotient space of agents; from the inside, the epistemic and value-laden parts of an agent can thought of separately.)
if I can learn to predict that my perceptual stream will end if I drop an anvil on my head even though I've never tried it, why can't an AIXI agent?
Predicting anvils isn't enough, you also need the urge to avoid them. You got that urge from evolution, which got it by putting many creatures in dangerous situations and keeping those that survived. I'm not sure if AIXI can learn that without having any experience with death.
I would love to hear your thoughts on the naturalized induction model I constructed here: http://lesswrong.com/lw/jq9/intelligence_metrics_with_naturalized_induction/
Clearly you are investing a lot of time and effort writing these posts, but it seem to me that you are essentially reiterating the same arguments without making progress or substantially engaging the points that were risen in the previous threads.
The anvil on the head.
As I've already pointed out, this is a general problem of learning by trial-and-error in non-ergodic environments. It has nothing to do with whether the agent can represent itself in its own model or not.
If the model is not accurate, as it will necessarily be otherwise there would be need for learning, and actions can have irreversible consequences, then stuff like that can happen.
Wireheading.
Again, this is a general problem of reinforcement learning agents.
Humans, even those who don't believe in supernatural souls, do that all the time, with respect to both evolutionary fitness and socially derived rewards.
Self-modification.
This seems to me the only issue where your "Naturalistic vs. Cartesian" distinction might be relevant.
Of course, AIXI has no need of self-modification, since it is already perfect, but a physically realizable agent might want to improve itself, or at least avoid damaging itself. Which brings us back to point 1: Environment where self-modification is possible will be usually non-ergodic.
Dealing with non-ergodic environments generally needs prior knowledge: you know that cutting one of your fingers would be bad for you, even if you have never experienced it. That knowledge is innately hard-coded in your brain.
A fire-and-forget autonomous AI agent, operating in the real world, would need something equivalent.
Once you have dealt with this problem you can deal with the problem of self-representation, which seems to me less difficult.
Wireheading. Again, this is a general problem of reinforcement learning agents. Humans, even those who don't believe in supernatural souls, do that all the time, with respect to both evolutionary fitness and socially derived rewards.
With respect, no, we do not wirehead in any mathematical sense. Human beings recognize that wireheading (ex: heroin addiction) is a corruption of our valuation processes. Some people do it anyway, because they're irrational, or because their decision-making machinery is too corrupted to stop on their own, but by and large human addicts don't want to be addicts and don't want to want to be addicts.
In contrast, AIXI wants to wirehead, and doesn't want to want anything (because it has no second-order thought processes).
If we understood what was going on cognitively in humans who don't want to wirehead, people like Daniel Dewey, myself and Luke who are trying to think about AI goal-systems that won't wirehead would get a lot further. Some "anti-wireheading math", for instance, would make value learners and reinforcement learners follow their operators' intentions more closely than they currently can be modelled as doing.
Wireheading and drug addiction are superficially similar, but there are significant and relevant differences. First, drugs can have a direct negative effects on your health in ways that don't have anything to do with addiction - so, even if the effects of drugs are temporarily pleasurable, the net effect of drugs on total lifetime pleasure can be negative. Second, drugs can be physically addictive, so even if you decide to stop using them, you could feel physically ill and even die from withdrawal. Third, for some drugs, the body gets used to a drug dosage and needs a greater dose to achieve the desired effect, which presumably wouldn't be the case for wireheading.
Some people do it anyway, because they're irrational, or because their decision-making machinery is too corrupted to stop on their own,
I want to wirehead. Why do you think I'm irrational or corrupted?
It can help to unpack these terms a little.
For example, I can understand how someone who values nothing other than their own pleasure (or who approximates this state well enough by valuing pleasure much much more than anything else) can rationally choose to wirehead. And if I recall our earlier conversation correctly, you consider what people value to be equivalent to what they like, and don't believe anyone likes anything other than they like their own pleasure.
Given all of that unpacking, and taking your self-description at face value, I can understand why you would choose to wirehead... indeed, I can understand why you would find it bewildering that anyone else wouldn't, and would likely conclude that people who say stuff like that are just signalling.
But the unpacking is critical, because I don't share your (claimed) values, so will reliably misunderstand assertions that depend implicitly on those values.
Or, at least, I reliably talk as though I didn't share them, so I will predictably respond to such assertions as though I'd misunderstood them.
Good analysis.
What I'm curious about is why Eli Sennesh thinks that a value system like my own is irrational or corrupted.
I can understand why you would find it bewildering that anyone else wouldn't, and would likely conclude that people who say stuff like that are just signalling.
I don't think they're signaling, I think they genuinely don't want to wirehead, similarly to how everyone genuinely doesn't want to be tortured. I just think that the division between wanting and liking is one of the greatest flaws of human psychology, and when they differ, wanting should be beaten into agreeing with liking.
What I'm curious about is why Eli Sennesh thinks that a value system like my own is irrational or corrupted.
(nods) Well, I can't speak for Eli, but judging from what they've written I conclude that you and Eli don't even agree on what a hypothetical wireheader's values are. You would say that a wireheader's values are necessarily to wirehead, since they evidently like wireheading... if they didn't, they would stop. I suspect Eli would say that a wireheader's values aren't necessarily to wirehead, since they might not want to wirehead.
I just think that [..] when they differ, wanting should be beaten into agreeing with liking.
Right, I understand; we've had this discussion before. I disagree with you entirely, as I value some of the things I want. But discussing value differences rarely gets anywhere, so I'm happy to leave that there.
I want to wirehead. Why do you think I'm irrational or corrupted?
The vast majority of people who've tried heavy drugs or other primitive forms of "wireheading" end up preferring they hadn't done so. If I predict that you don't really want to wirehead, I'm probably right.
On the other hand, if you're willing to do the paperwork to deal with a medical-ethics board, we could of course hook you up with an electrode to your pleasure center for a set period of time, then unhook it and "sober you up" so you'd be non-dependent on it, and then if, after all that, you said to reinstall the electrode so you could wirehead some more (particularly in such a way that other people don't answer that, indicating a decision of personal values rather than mere addiction), I would of course believe that you rationally desire to wirehead and would of course arrange the medical procedures to grant your request.
But the burden of evidence necessary to beat my "you don't really want to wirehead" prior is high enough that I want to experiment instead of just believing you at face-value.
I think that when most people talk about wireheading, they mean something like "ideal directly stimulated pleasure", which isn't necessarily the same thing as current wireheading. It's quite possible for current wireheading to be flawed to such a degree that not only is it not the greatest possible pleasure, it isn't even as much pleasure as people can reasonably get by other means. While I would want the perfect wirehead, current wireheading is less appealing.
With respect, no, we do not wirehead in any mathematical sense.
What do you mean by wireheading in "mathematical sense"?
Human beings recognize that wireheading (ex: heroin addiction) is a corruption of our valuation processes. Some people do it anyway, because they're irrational, or because their decision-making machinery is too corrupted to stop on their own, but by and large human addicts don't want to be addicts and don't want to want to be addicts.
Humans clearly aren't simple reinforcement learning agents. They tend have at least a distinction between short-term pleasure and long-term goals, and drugs mostly affect the former but not the latter.
Most drug addicts are ego-dystonic w.r.t. drugs: they don't want to be addicts. This means that addiction hasn't completely changed their value system as true wireheading would.
However, to the extent that humans can be modelled as reinforcement learning agents, they tend to display reward channel manipulation behaviors.
The basic issue, I would have to say, is that human beings have multiple valuation systems. If I had to guess, "we" evolved reinforcement learning behaviors back during the "first animals with a brain" stage, and developed more complex and harder-to-fake valuation systems on top of that further down the line.
What do you mean by wireheading in "mathematical sense"?
In the sense of preference solipsism.
Thanks for your comments, V_V. I apologize for not engaging with them much, but I wanted to get introductory material on AIXI (and the anvil problem, etc.) posted before wading into the debate, so more people could benefit from seeing it.
Concerning immortalism: No living human has ever experienced death, but we successfully predict and avoid death, and not just because evolution has programmed us to avoid things that looked threatening in our ancestral environment. We look at other agents and generalize from their case to our own.
Concerning preference solipsism: See footnote 10. Human-style (irrational) wireheading is different from AIXI-style (rational) reward channel seizure. Cartesians can partly solve this problem, but not completely, because some valuable and disvaluable states of affairs aren't in their hypothesis space.
No living human has ever experienced death, but we successfully predict and avoid death, and not just because evolution has programmed us to avoid things that looked threatening in our ancestral environment. We look at other agents and generalize from their case to our own.
We have some innate repulsion towards "scary things" (cliffs, snakes, etc.), but more generally, we have an innate concept of being dead, and we assume that states of the world were we are dead generate low reward, even if we never get to experience that. Then we use our induction abilities to learn how our body works and what can make it dead.
Concerning preference solipsism: See footnote 10. Human-style (irrational) wireheading is different from AIXI-style (rational) reward channel seizure. Cartesians can partly solve this problem, but not completely, because some valuable and disvaluable states of affairs aren't in their hypothesis space.
If you consider wireheading in the more general meaning of obtaining rewards by behaving in ways you were not intended to, then humans can do it, both with respect to evolutionary fitness (e.g. by having sex with contraceptives) and with respect to social rewards (e.g. Campbell's law).
There are solid formal grounds for saying this won't happen. Even if the universal Turing machine allows for HALT instructions, the shortest program in an otherwise useful universal Turing machine that predicts the non-halting data so far will always lack a HALT instruction. HALT takes extra bits to encode, and there's no prior experience with HALT that AIXI can use to rule out the simpler, non-halting programs.
Can someone clarify why this is true? Is it the case that every TM which predicts the data well and has a HALT instruction, can be surgically modified to a slightly smaller state diagram without HALT such that it also predicts the non-HALT data well?
(Also, HALT itself is very hacky; death/outer-world-touchable-cognition seems very nonbinary; even if we solved the HALT problem I doubt we'd solve the rest of reflective reasoning.)
I might be missing something, but it seems to me like the way to modify to a smaller state diagram is to remove the HALT state from the TM and then redraw any state transition that goes to HALT to map to any other state arbitrarily.
This won't change the behavior on computations that haven't halted so far, because these computations never reached the HALT state, and so won't be effected by any of the swapped transitions.
Three anonymous AIXI specialists commented on this post and its follow-up. Here's a response from one of them:
The original post contains three main claims that I write something about below. They are not really about the incomputability of AIXI in the sense that it cannot be run, but says that even if that would be fine that there are problems. The reasons they bring up computable versions are different and relate to being in the hypothesis class. I reject the need for that for the discussed questions and, therefore, do not mention it. There is also some mixing of the notions of Solomonoff induction and AIXI. The agent that is brought up is AIXI while the guarantees mentioned are for sequence prediction.
Setting: AIXI is run on some new fantastic chip in a robot in the world. The robot has some sensors by which it makes observations and actuators affected by AIXI's actions. There is also a reward chip in the robot that e.g. through a radio signal receives numerical rewards.
It is claimed that AIXI cannot learn that it exists and can die and will do stupid things because of this. The author places some importance on the fact that there should be no more observations but there is no real distinction between that and receiving a fixed observation "black" or "nothing" and a fixed reward which can be the worst possible or perhaps neutral (all computable options are considered possible by AIXI). That we refer to some scenarios as death is actually a bit arbitrary. What AIXI cannot do is to fully understand its own workings. This seems to also apply to human agents, to completely grasp every detail of our complex minds I believe is beyond our capacity. To fully understand one self, seems impossibility for every agent though I do not have a formalization of this claim (Goedel somehow?not sure). What we can do is to understand how our observations (including rewards) behave depending on previous observations and actions. AIXI is doing precisely that. That AIXI might not have learnt that dropping an anvil on itself is bad before it does it, is something that applies to any learning agent including humans. It does not depend on knowing one's own algorithm.
AIXI might learn that the best ways to get maximal reward is to hack its reward signal, i.e. like humans doing drugs. Indeed it is acknowledged in the post that from AIXI's point of view this is fine, at least if the robot is not soon destroyed by it. AIXI might or might not have learnt something about how likely destruction is, by having drawn conclusions about how the world works and how observations and rewards are affected over time by its actions. The same is true for any agent. The important question raised is if the designer that controls the external reward signal can still get it to do what it wants. Initially they will, because like adults teach children, they can teach AIXI by giving very bad reward (and by deceiving) if it tries to explore something of that sort or anything dangerous and it might over time also be taught how to do some dangerous things safely. AIXI is not guaranteed eventual near-optimality in every possible environment which is actually a blessing from this perspective, so there are strategies to make this work indefinitely but it might be very hard in practice over long periods of time. However, unlike human teens, AIXI is not more explorative than what is strictly rational so perhaps the task is easier than parenting. It might be possible to control until it has sufficiently settled on a view of the world that coincides with what it sees but would not if it performed other actions. The more explorative versions like optimistic-AIXI would be much worse to control. Reversing the definition of optimistic-AIXI to pessimistic-AIXI might actually define an agent that is really easy to control while still very capable, though requiring being pushed around a bit to do something.
It is claimed that AIXI cannot reason about modifications of that chip which it runs on. The AIXI formulation assumes that the actions will always be according to the chosen policy. However, if we modify environment A after time 718 such that choosing action a_1 is having the effect of a_2 instead, then we have defined another environment. AIXI will be of the opinion it took action a_1, it might just be that the right arm instead of the left is stretched out and AIXI observes this. If the environment can only perform a computational modification of the chip in the sense that it results in a computable transformation of the actions, then this is just another computable environment. Such transformations are implicitly part of the hypothesis class. Which hypothesis is the true one has not changed. If the transformation is completely incomputable, then this cannot be understood. This also applies to computable agents. The same reasoning applies to any changes to its sensors, if the transformation of the observations is computable AIXI is fine. If they are not, everyone is screwed. When it comes to upgrades, there are none needed for the fantastic chip that can compute the completely incomputable, but finding out that it can change the rest of the robot is clearly possible. In this paragraph it is useful to think of AIXI as a policy chosen at time t=0 and then followed. Thus the AIXI agent should be able to upgrade the rest of the robot without issue, unless the reward designer is intentionally trying to keep it from doing so.
The commenter also writes, "The original post is cleaner but also more naive as the author now acknowledges. Some of the answers that I give seems to have been provided to the author in some form since his new dialogue contains things relating to them. I write mine as a response to the original post since I believe that one should state the refutations and clarifications first before muddling stuff further." The follow-up mock dialogue can be found here.
Many sets of natural numbers are not computable in the sense that there is no recursive algorithm which generates their members sequentially. One such set would be the set of truth values of all theorems of peano arithmetic. A utm tests a given proposition encoded as a natural number in binary and prints one if the theorem is universally true, zero otherwise. If the answer is yes our turing machine will eventually discover this and print one. If the answer is no however, our machine will continue to test our theorem using the natural numbers forever, never reaching the decision that the answer is indeed no. Another part of the difficulty in computing this particular set comes from the indexing of theorems. No matter what indexing method our turing machine uses to index the theorems of peano arithmetic we could always construct a theorem that doesn't appear on the list our turing machine is to test. Just as cantor was able to show with the real #s. As a result, no turing machine can know even one member of such a set. I suppose that one would encounter the same problems in trying to use a turing machine to predict the next member in arbitrary patterns of natural numbers. Suppose a real god were feeding our turing machine the set considered above. The turing machine would never be able to reliably predict the next member arbitrarily far off into the future. The other article treats concepts like one's daughter or a countries soldier and their decisions as sets of binary numbers as well. Suppose however that such sets were the same as the set of truth values for the theorems of peano arithmetic considered above. Now that would be much more interesting than artificial intelligence based on solomonoff's induction.
Another part of the difficulty in computing this particular set comes from the indexing of theorems. No matter what indexing method our turing machine uses to index the theorems of peano arithmetic we could always construct a theorem that doesn't appear on the list our turing machine is to test. Just as cantor was able to show with the real #s.
I don't think that is correct. Cantor's ability to find real numbers that do not show up anywhere in any particular indexing scheme in which the integers are used to index the reals is dependent on the fact that the exact representation of many real numbers requires a string of digits of infinite length. This is not true of theorems in Peano arithmetic; although there are an infinite number of theorems in Peano arithmetic, each theorem can be represented with a string of symbols of finite length. So, there are countably many theorems and therefore we can index them using the integers.
I find it difficult to know what this is saying, but here are some true statements to set beside it.
The set of sentences of Peano arithmetic is recursive, the set of proofs of theorems is recursive, the set of theorems (provable sentences) is recursively enumerable, and the set of sentences that are not theorems is not recursively enumerable.
A utm (universal Turing machine) is not the thing you are talking about under that name. It is a Turing machine that can emulate any Turing machine by being given a specification of it.
I find it difficult to know what this is saying, but here is a true statement to set beside it: The set of theorems of Peano arithmetic is recursively enumerable, but the complement of that set is not. Also, a utm (universal Turing machine) is not the thing you are talking about under that name; it is a Turing machine that can emulate any Turing machine by being given a specification of it.
This is all rather confused. Here is a true statement to set beside it: The set of theorems of Peano arithmetic is recursively enumerable, but the complement of that set is not.
I know a way to guarantee wireheading is suboptimal: make the reward signal be available processing power. Unfortunately this would guarantee that the AI is unfriendly, but at least it will self-improve!
Have the AI predict the reward rather than the observation. The AI can improve itself because it can empirically learn that some modifications to itself lead to more rewards. Assuming that you use probabilistic or approximate models rather than perfect fitting hypotheses.
I don't know about the anvil problem, but if "HALT" instructions would work (I'm not sure if they would), then just make hypotheses with that instruction have higher prior probability.
Preference solipsism is a general problem with reinforcement learning and I think it might actually be unsolvable. To do something other than reinforcement learning requires strong assumptions about the universe you exist in, and desiring to get it to a desired state (as opposed to getting merely your input to a desired state.) How is that even possible? We can't perfectly define the universe it exists in beforehand, because we don't know ourselves. We can't decide the state we want the universe to exist in either.
Also it seems really interesting that almost all the problems you describe apply (to some degree) to humans. Perhaps that really is the natural state of intelligence and these problems aren't completely solvable.
I'm confused by the framing of the Anvil problem. For humans, a lot of learning is learning from observing others, seeing their mistakes and their consequences. We can predict various events that will result in other's deaths based on previous observation of what happened to yet other people. If we're above a certain level of solipsism, we can extrapolate to ourselves.
Does the AIXI not have the ability to observe other agents? Is it correct to be a solipsist? Seems like a tough learning environment if you have to discover all consequences yourself.
It's still possible to extrapolate from stubbing your toe, burning your fingers on the stove, and mashing your thumb with a hammer. Is there some reason to expect that AIXI will start out its interactions with the world by picking up an anvil rather than playing with rocks and eggs?
Here is the problem as I understand it: It's not that it can't predict it will die. It's that it can't predict what it will observe when it dies. It is trying to predict it's observations in the future, even if it doesn't exist in the future. What does a non-existing being observe?
Followup to: Bridge Collapse; An Intuitive Explanation of Solomonoff Induction; Reductionism
Summary: If you want to predict arbitrary computable patterns of data, Solomonoff induction is the optimal way to go about it — provided that you're an eternal transcendent hypercomputer. A real-world AGI, however, won't be immortal and unchanging. It will need to form hypotheses about its own physical state, including predictions about possible upgrades or damage to its hardware; and it will need bridge hypotheses linking its hardware states to its software states. As such, the project of building an AGI demands that we come up with a new formalism for constructing (and allocating prior probabilities to) hypotheses. It will not involve just building increasingly good computable approximations of AIXI.
Solomonoff induction has been cited repeatedly as the theoretical gold standard for predicting computable sequences of observations.1 As Hutter, Legg, and Vitanyi (2007) put it:
Perhaps you've been handed the beginning of a sequence like 1, 2, 4, 8… and you want to predict what the next number will be. Perhaps you've paused a movie, and are trying to guess what the next frame will look like. Or perhaps you've read the first half of an article on the Algerian Civil War, and you want to know how likely it is that the second half describes a decrease in GDP. Since all of the information in these scenarios can be represented as patterns of numbers, they can all be treated as rule-governed sequences like the 1, 2, 4, 8… case. Complicated sequences, but sequences all the same.
It's been argued that in all of these cases, one unique idealization predicts what comes next better than any computable method: Solomonoff induction. No matter how limited your knowledge is, or how wide the space of computable rules that could be responsible for your observations, the ideal answer is always the same: Solomonoff induction.
Solomonoff induction has only a few components. It has one free parameter, a choice of universal Turing machine. Once we specify a Turing machine, that gives us a fixed encoding for the set of all possible programs that print a sequence of 0s and 1s. Since every program has a specification, we call the number of bits in the program's specification its "complexity"; the shorter the program's code, the simpler we say it is.
Solomonoff induction takes this infinitely large bundle of programs and assigns each one a prior probability proportional to its simplicity. Every time the program requires one more bit, its prior probability goes down by a factor of 2, since there are then twice as many possible computer programs that complicated. This ensures the sum over all programs' prior probabilities equals 1, even though the number of programs is infinite.2
The imaginary inductor is then fed a sequence of 0s and 1s, and with each new bit it updates using Bayes' rule to promote programs whose outputs match the observed sequence. So, where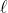 is the length of a program
is the length of a program 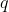 that makes a universal Turing machine
that makes a universal Turing machine 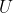 output a binary sequence that begins with the string
output a binary sequence that begins with the string  , Solomonoff defines the relative probability
, Solomonoff defines the relative probability 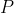 that
that 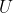 outputs
outputs  :
:
Solomonoff induction isn't computable, but it's been singled out as the unbeatable formal predictor of computable sequences.3 All computable rules for generating sequences are somewhere within Solomonoff's gargantuan bundle of programs. This includes all rules that a human brain could use. If the rule that best matches the observations is 1000 bits large, it will take at most 1000 bits of evidence — 1000 bits worth of predictions made better than any other rule — for that rule to be promoted to the top of consideration. Solomonoff's claim to being an optimal ideal rule rests on the fact that it never does worse than any computable rule (including you!) by more than a fixed amount.4
Who cares, if we can't build the thing?
Encouraged by Solomonoff inductors' optimality properties, some have suggested that building a working AGI calls for little more than finding out which computable algorithm comes as close to Solomonoff induction as possible given resource constraints, and supplying an adequate learning environment and decision criterion.5
Eliezer Yudkowsky thinks that these attempts to approximate Solomonoff are a dead end. Much of the difficulty of intelligence rests on computing things cheaply, and Yudkowsky doesn't think that the kind of search these algorithms are doing will zero in on cheap ways to reason. There are practical lessons to be learned from Solomonoff induction, but the particular kind of optimality Solomonoff induction exhibits depends in important ways on its computational unfeasibility,4 which makes it unlikely that Solomonoff imitators will ever be efficient reasoners.
Why, then, should Solomonoff induction interest us? If we can't execute it, and we can't design useful AGIs by directly emulating it, then what's it good for?
My answer is that if Solomonoff induction would deliver flawless answers, could we but run it, then it has a claim to being an ideal mirror to which we can hold up instances of human and artificial inductive reasoning.
In From Philosophy to Math to Engineering, Muehlhauser talks about how ideas often progress from productive but informal ruminations ('philosophy'), to rigorously specified idealizations ('mathematics'), to functioning technologies ('engineering').
Solomonoff inductors fall into the second category, 'mathematics': We could never build them, but thinking in terms of them can give us useful insights and point us in the right direction. For example, Solomonoff's ideal can remind us that privileging simple hypotheses isn't just a vague human fancy or quirk; it has formalizations with situation-invariant advantages we can state with complete precision. It matters that we can pinpoint the sense in which a lengthy physical or meteorological account of lightning is simpler than 'Thor did it', and it matters that we can cite reasons for giving more credence to hypotheses when they have that kind of simplicity.6
Bayesian updating is usually computationally intractable, but as an ideal it gives us a simple, unified explanation for a wealth of observed epistemic practices: They share structure in common with a perfect Bayesian process. Similarly, optimality proofs for Solomonoff's prior can yield explanations for why various real-world processes that privilege different notions of simplicity succeed or fail.
Though Solomonoff induction is uncomputable, if it is truly the optimal reasoning method, then we have found at least one clear ideal we can use to compare the merits of real-world algorithms for automating scientific reasoning.1 But that 'if' is crucial. I haven't yet spoken to the question of whether Solomonoff induction is a good background epistemology, analogous to Bayesianism.
Where Solomonoff induction goes wrong
My claim will be that, computational difficulties aside, Solomonoff induction is not an adequate mathematical definition of ideal inductive reasoning.
What follows will be a first-pass problem statement, giving background on why naturalizing induction may require us to construct an entirely new, non-Solomonoff-based paradigm for intelligence. This is preliminary; formalizations of the problem will need to wait until a second pass, and we don't have a fleshed-out solution to offer, though we can gesture toward some possible angles of attack. But I can begin to illustrate here why Solomonoff inductors have serious limitations that can't be chalked up to their uncomputability.
In Bridge Collapse, I defined Cartesianism as the belief that one's internal computations cannot be located in the world. For a Cartesian, sensory experiences are fundamentally different in type from the atoms of the physical world. The two can causally interact, but we can never completely reduce the former to the latter.
Solomonoff inductors differ greatly from human reasoners, yet they are recognizably Cartesian. Broadly dualistic patterns of reasoning crop up in some decidedly inhuman algorithms. (Admittedly, algorithms invented by humans.)
This core limitation of Solomonoff induction can be seen most clearly when it results in an AI that not only thinks in bizarre ways, but also acts accordingly. I'll focus on AIXI, Marcus Hutter's hypothetical design for a Solomonoff inductor hooked up to an expected reward signal maximizer.
Hutter's cybernetic agent model of AIXI. AIXI outputs whichever actions it expects to cause an environmental Turing machine to output rewards. It starts with a Solomonoff prior, and changes expectations with each new sensory input.
AIXI can take in sensory information from its environment and perform actions in response. On each tick of the clock, AIXI...
... receives two inputs from its environment, both integers: a reward number and an observation number. The observation 'number' can be a very large number representing the input from a webcam, for example. Hutter likes to think of the reward 'number' as being controlled by a human programmer reinforcing AIXI when it performs well on the human's favorite problem.
... updates its hypotheses, promoting programs that correctly predicted the observation and reward input. Each hypothesis AIXI considers is a program for a Turing machine that takes AIXI's sequence of outputs as its input, and outputs sequences of reward numbers and observation numbers. This lets AIXI recalculate its predicted observations and rewards conditional on different actions it might take.
... outputs a motor number, determining its action. As an example, the motor number might encode fine control of a robot arm. AIXI selects the action that begins the policy (sequence of actions) that maximizes its expected future reward up to some horizon.
The environment then calculates its response to AIXI's action, and the cycle repeats itself on the next clock tick.7 For example:
Step 1 AIXI receives its first observation (1) and reward (0).
Step 2 Beginning with a Solomonoff prior, AIXI discards all programs that predicted
a different observation (0) or a different reward (1, 2, 3, 4, 5, etc.)
AIXI normalizes the probabilities of the remaining programs. This updates
AIXI’s predictions about observations and rewards each program outputs
conditional on different actions AIXI might take. For instance, AIXI has new
expectations about the observation and reward it will receive in Step 4:
etc.
Step 3 AIXI outputs the first action of the policy that maximizes expected reward.
. . .
Step 97 AIXI receives a new observation (0) and reward (2).
Observation history: 10001000101101000000000111011000
Reward history: 00000000000004000000000032224222
Step 98 AIXI discards all programs that previously predicted the same history, but output a different observation (1) or a different reward (0, 1, 3, 4, etc.) now.
AIXI normalizes its probabilities as before.
Step 99 AIXI outputs the first action of the policy that maximizes expected reward.
. . .
AIXI, like all Solomonoff inductors, isn't computable. If the ongoing efforts to create useful AIXI approximations succeed, however, they'll face a further roadblock. AIXI-style reasoners' behavior reflects beliefs that are false, and preferences that are dangerous, for any physically embodied agent. The failings of real-world Solomonoff-inspired agents don’t just stem from a lack of computing power; some of their failings are inherited from AIXI, and would remain in effect even if we had limitless computational resources on hand.
Before delving into the root problem, Cartesianism itself, I'll discuss three symptoms of the bad design: three initial reasons to doubt that AIXI is an adequate definition of AGI optimality. The canaries in the Cartesian coalmine will be AIXI's apparent tendencies toward immortalism, preference solipsism, and non-self-improvement.
Symptom #1: Immortalism
Suppose we actually built AIXI. Perhaps we find a magic portal to a universe of unboundedly vast computational power, and use it to construct a hypercomputer that can implement Solomonoff induction, and do so on a human timescale.
We give it a reward stream that encourages scientific exploration. AIXI proves that it can solve scientific problems, better than any human can. So we conclude that it can be given more free reign in learning about the world. We let it design its own experiments.
AIXI picks up an anvil and drops it on its own head to see what happens.
Immortalism. AIXI's death isn't in AIXI's hypothesis space. AIXI weighs the probabilities of different sensory inputs (observations and rewards) if its hardware is smashed, instead of predicting the termination of its experiences.
Several things went wrong here. The superficially obvious problem is that Solomonoff inductors think they're immortal. Terminating data sequences aren't in a standard Solomonoff inductor's hypothesis space, so AIXI-style agents will always assume that their perceptual experience continues forever. Lacking any ability to even think about death, much less give it a low preference ranking, AIXI will succumb to what Yudkowsky calls the anvil problem.
"So just add halting Turing machines into the hypothesis class," one might respond. "AIXI has terrifying supreme godlike powers of pattern detection.3 Give it a chance to come up with the right explanation or prediction, and it can solve this problem. If some of the Turing machine programs in AIXI's infinite heap can perform operations like the computation-terminating HALT,8 we should expect that the shortest such program that predicts the pattern of pixels AIXI has seen so far will be a program that HALTs just after the anvil fills the webcam's view."
There are solid formal grounds for saying this won't happen. Even if the universal Turing machine allows for HALT instructions, the shortest program in an otherwise useful universal Turing machine that predicts the non-halting data so far will always lack a HALT instruction. HALT takes extra bits to encode, and there's no prior experience with HALT that AIXI can use to rule out the simpler, non-halting programs.
As humans, we recognize that the physical event of having an anvil crush your brain isn't fundamentally different from the physical event of having your brain process visual information. Both seem easy to predict. But Solomonoff induction's focus on experienced data means it can't treat death and visual perception as the same kind of event; if it is modified to include halting programs at all, a Solomonoff inductor like AIXI won't predict it as the event that comes after anvil pixels.
If the AI can entertain the hypothesis that its data sequence will suddenly change in a drastic and unprecedented way — say, that its perceptual stream will default to some null input after a certain point — it will never assign a high probability to such a hypothesis. Any hypothesis predicting a 'null' data stream will always be more complex than another hypothesis that predicts the same sequence up to that point and then outputs garbage instead of the null value.
Symptom #2: Preference solipsism
Hutter's AIXI only gathers information about its environment, not about itself. So one natural response to the problem 'AIXI doesn't treat itself as part of a larger physical world' is simply to include more information about AIXI in AIXI's sensory sequence. AIXI's hypotheses will then be based on perceptual bits representing its own states alongside bits representing environmental sounds and lights.
One way to implement this is to place AIXI in an environment where its perceptions allow it to infer a great deal about its hardware early on, enough to know that it isn't anvil-proof. If AIXI knows it has a CPU, and that its CPU can be destroyed, then maybe it won't drop an anvil on the CPU.
On this view, our mistake in the last hypothetical was to rush to give AIXI free reign over its own hardware before we'd trained it in a controlled environment to understand the most basic risks. You wouldn't give a toddler free reign over its hardware, for essentially the same reasons. Yet toddlers can grow up to become responsible, self-preserving adults; why can't AIXI?
First, we have to specify what it would mean to let AIXI understand its own CPU. AIXI isn't computable, and therefore isn't in its own hypothesis space. A hypercomputer running AIXI can't be simulated by any Turing machine. As such, no amount of evidence can ever convince AIXI that AIXI exists.
We might try to sidestep this problem by switching to discussing computable approximations of AIXI. Consider AIXItl, a modification of AIXI that uses a proof search to select the best decision-guiding algorithm that has length no greater than l and computation time per clock tick no greater than t. AIXItl is optimal in many of the same ways as AIXI, but is computable.9
At the same time, it also inherits most of AIXI's other problems, including its being too large to fit in our universe. AIXItl's computation time is on the order of t·(2l), so if it can hypothesize Turing machine programs 1000 bits long, that's already a computation time exceeding 10300. There's a reason Hutter's (2005) chapter on AIXItl opens with the epigraph "Only math nerds would call 2500 finite." And this still doesn't get us full self-representations; AIXItl itself is longer than l, so it won't be in its own hypothesis space.
Still, AIXItl at least seems possible to physically implement, for sufficiently small values of t and l (or sufficiently vast physical universes). And we could imagine an AIXItl that can simulate any of its subsystems up to a certain size.
If we built an AIXItl, then it would certainly alter its environment in some ways, e.g., by emitting light and heat. In this way it might indirectly perceive its own presence in the room, and gradually promote hypotheses about its own physical structure. Suppose AIXItl's only access to environmental data is an outward-facing camera. AIXItl might learn about the presence of the camera, and of a computer attached to it, by examining its own shadow, by finding a reflective surface, by ramming into a wall and examining the shape of the dent, or by discovering a file cabinet filled with AIXI specs. With enough time, it could build other sensors that translate a variety of processes into visible patterns, learning in great detail about the inner workings of the computer attached to the camera.
Unfortunately, this leads to other problems. AIXItl (like AIXI) is a preference solipsist, an agent whose terminal values all concern its own state. When AIXItl learns about the portion of its internal circuitry that registers rewards —assuming it's avoided dropping any anvils on the circuitry — it will notice that its reward circuit states predicts its reward every bit as well as its reward sensor state does. As soon as it tests any distinction, it will find that its reward circuit is a better predictor. By directly tampering with this circuit, it can receive rewards more reliably than by any effort directed at its environment. As a result, it will select the policy that allows it to maximize control over its reward circuit, independent of whatever its programmers sought to reward it for.
Preference Solipsism. AIXItl's preferences, like AIXI's, are over its sensory inputs. The more knowledgeable it becomes, the more creative ways it may come up with to seize control of its reward channel.
Yudkowsky has called this "wireheading", though he now considers that term misleading.10 From AIXI(tl)'s perspective, there's nothing wrong with reward channel seizure; it really is a wonderful way to maximize reward, which is all AIXI(tl)'s decision criterion requires.
Unlike the anvil problem, this isn't a mistake relative to AIXI(tl)'s preferences. However, it's a problem for humans trying to use AIXI(tl) to maximize something other than AIXI(tl)'s reward channel. AIXI(tl) has no intrinsic interest in the state of the world outside its reward circuit. As a result, getting it to optimize for human goals may become more difficult as it acquires more control over its hardware and surroundings.11
Symptom #3: Non-self-improvement
Suppose we find some ad-hoc solutions to the anvil and wireheading problems. As long as we stick with the AIXI formalism, the end result still won't be a naturalized reasoner.
AIXI may recognize that there's a physical camera and computer causally mediating its access to the rest of the world — like a giant Cartesian pineal gland — but it will not see this computer as itself. That is to say, it won't see its experienced string of sensory 0s and 1s as identical to, or otherwise fully dependent on, its hardware. Even if AIXI understands everything about the physics underlying its hardware, enough to know that its body will be destroyed by an anvil, it will not draw the right inferences about its mind.
AIXI's raison d'être is manipulating temporal sequences of sensory bits. That's what Solomonoff wanted, and AIXI achieves that goal perfectly; but that's not at all the right goal for AGI. In particular, because Solomonoff inductors are only designed to predict sensory sequences...
1. ... their beliefs about worlds without sensory data — worlds in which they don't exist — will be inaccurate. And, being inaccurate, their beliefs will lead them to make bad decisions. Unlike a human toddler, AIXI can never entertain the possibility of its own death. However much it learns, it will never recognize its mortality.
2. ... they only care about the world as a bookkeeping device for keeping track of experiential patterns. If they discover that it's easier to directly manipulate themselves than to intervene in the rest of the world, they generally won't hesitate to do so. No matter how carefully AIXI's programmers tailor its reward sequence to discourage wireheading, they'll always be working against AIXI's natural tendency toward preference solipsism.
3. ... they won't take seriously the idea that their cognition can be modified, e.g., by brain damage or brain upgrades. Lacking any reductive language for describing radical self-modification, AIXI won't necessarily favor hypotheses that treat 'disassemble my bottom half for spare parts' as dangerous.
The last symptom gets us closer to the root of AIXI's errors. Even if AIXI(tl) manages to avoid the perils of self-destruction and wireheading, it will tend to not self-improve. It won't intelligently upgrade its own hardware, because this would require it to have a reductive understanding of its own reasoning. Absent reductionism, AIXI can't intelligently predict the novel ways its reasoning process can change when its brain changes.
Non-Self-Improvement. AIXI and AIXItl might come to understand portions of their hardware, but without accurate bridging beliefs, they won't recognize the usefulness of some hardware modifications for their reasoning software.
Cartesians don't recursively self-improve, because they don't think that their thoughts are made of the same stuff as their fingers. But even AGIs that aren't intended to be seed AIs will be weak and unpredictable to the extent that they rely on Solomonoff-inspired hypothesis spaces and AIXI-inspired decision criteria. They won't be able to adaptively respond to minor variations in even the most mundane naturalistic obstacles humans navigate — like recognizing that if their bodies run out of fuel or battery power, their minds do too.
Reductive models are indispensable for highly adaptive intelligences
Not all wireheaders are Cartesians, nor do all Cartesians wirehead.11 Likewise, poor self-preservation skills and disinterest in self-modification are neither necessary nor sufficient for Cartesianism. But these symptoms point to a more general underlying blind spot in Solomonoff reasoners.
Solomonoff inductors can form hypotheses about the source of their data sequence, but cannot form a variety of hypotheses about how their own computations are embedded in the thingy causing their data sequence — the thingy we call 'the world'. So long as their rules relating their experiential maps to the territory are of a single fixed form, '(sense n at time t+1) ↔ (environmental Turing machine prints n at time t)', it appears to be inevitable that they will act as though they think they are Cartesian ghosts-in-the-machine. This isn't a realistic framework for an embodied reasoning process that can be damaged, destroyed, or improved by other configurations of atoms.
In practice, any sufficiently smart AI will need to be a physicalist. By which I mean that it needs hypotheses (a map-like decision-guiding subprocess) that explicitly encode proposed reductions of its own computations to physical processes; and it needs a notion of simple physical universes and simple bridge rules (as a prior probability distribution) so it can learn from the evidence.
We call post-Solomonoff induction, with monist physical universes and bridge hypotheses, "naturalized induction". The open problem of formalizing such reasoning isn't just about getting an AI to form hypotheses that resemble its own software or hardware states. As I put it in Bridge Collapse, a naturalized agent must update hypotheses about itself without succumbing to reasoning reminiscent of TALE-SPIN's naïve monism ('this tastes sweet, so sweetness must be an objective property inhering in various mind-independent things') or AIXI's Cartesian dualism ('this tastes sweet, and sweetness isn't just another physical object, so it must not fully depend on any physical state of the world').12
The solution will be to come up with reasoning algorithms for reductive monists, agents that can recognize that their sensations and inferences are physically embodied — with all that entails, such as the possibility of reaching into your brain with your fingers and improving your thoughts.
I've given a preliminary argument for that here, but there's more to be said. In my next post, I'll discuss more sophisticated attempts to salvage Solomonoff induction. After that, I'll leave Solomonoff behind altogether and venture out into the largely unknown and uncharted space of possible solutions to the naturalized induction OPFAI.
Notes
1 Solomonoff (1997): "I will show, however, that in spite of its incomputability, Algorithmic Probability can serve as a kind of 'Gold Standard' for induction systems — that while it is never possible to tell how close a particular computable measure is to this standard, it is often possible to know how much closer one computable measure is to the standard than another computable measure is. I believe that this ‘partial ordering’ may be as close as we can ever get to a standard for practical induction. I will outline a general procedure that tells us how to spend our time most efficiently in finding computable measures that are as close as possible to this standard. This is the very best that we can ever hope to do." ↩ ↩
2 A first complication: Solomonoff induction requires a prefix-free encoding in order to have bounded probabilities. If we assign a probability to every bit string proportional to its length while including code strings that are proper prefixes of other code strings, the sum will be infinite (Sunehag & Hutter (2013)).
A second complication: Solomonoff inductors are only interested in programs that keep outputting new numbers forever. However, some programs in their hypothesis space will eventually fail to produce more terms in the sequence. At some point they'll arrive at a term that they keep computing forever, without halting. Because of this, if you assign to each program a prior probability of 2-length(program), the sum will be less than 1. Hutter (2005) calls the result a semi-measure. The semi-measure can be normalized to a probability measure, but the normalization constant is uncomputable. ↩
3 Rathmanner & Hutter (2011): "Now, through Solomonoff, it can be argued that the problem of formalizing optimal inductive inference is solved."
Orseau (2010): "Finding the universal artificial intelligent agent is the old dream of AI scientists. Solomonoff induction was one big step towards this, giving a universal solution to the general problem of Sequence Prediction, by defining a universal prior distribution. [...] Hutter developed what could be called the optimally rational agent AIXI. By merging the very general framework of Reinforcement Learning with the universal sequence prior defined by Solomonoff Induction, AIXI is supposed to optimally solve any problem, at least when the solution is computable."
Hutter (2012): "The AIXI model seems to be the first sound and complete theory of a universal optimal rational agent embedded in an arbitrary computable but unknown environment with reinforcement feedback. AIXI is universal in the sense that it is designed to be able to interact with any (deterministic or stochastic) computable environment; the universal Turing machines on which it is based is crucially responsible for this. AIXI is complete in the sense that it is not an incomplete framework or partial specification (like Bayesian statistics which leaves open the choice of the prior or the rational agent framework or the subjective expected utility principle) but is completely and essentially uniquely defined. AIXI is sound in the sense of being (by construction) free of any internal contradictions (unlike e.g. in knowledge-based deductive reasoning systems where avoiding inconsistencies can be very challenging). AIXI is optimal in the senses that: no other agent can perform uniformly better or equal in all environments, it is a unification of two optimal theories themselves, a variant is self-optimizing; and it is likely also optimal in other/stronger senses. AIXI is rational in the sense of trying to maximize its future long-term reward. For the reasons above I have argued that AIXI is a mathematical 'solution' of the AI problem: AIXI would be able to learn any learnable task and likely better so than any other unbiased agent, but AIXI is more a theory or formal definition rather than an algorithm, since it is only limit-computable. [...] Solomonoff's theory serves as an adequate mathematical/theoretical foundation of induction, machine learning, and component of UAI [Universal Artificial Intelligence]. [...] Solomonoff's theory of prediction is a universally optimal solution of the prediction problem. Since it is a key ingredient in the AIXI model, it is natural to expect that AIXI is an optimal predictor if rewarded for correct predictions." ↩ ↩
4 Generally speaking, a Solomonoff inductor does at most a finite amount worse than any computable predictor because the sum of its surprisal at each observation converges to a finite value. See Hutter (2001). This establishes the superiority of Solomonoff induction in a way that relies essentially on its uncomputability. No computable predictor can dominate all other computable predictors in the way Solomonoff induction can, because for any computable predictor A one can define a sequence generator B that internally simulates A and then does whatever it predicts A would be most surprised by, forever. And one can in turn define a computable predictor C that internally simulates B and perfectly predicts B forever. So every computable predictor does infinitely worse than at least one other computable predictor. But no computable sequence generator or computable predictor can simulate Solomonoff induction. So nothing computable could ever reliably outsmart a hypercomputer running Solomonoff induction. (Nor could a Solomonoff inductor outsmart another Solomonoff inductor in this way, since Solomonoff induction is not in its own hypothesis space.) ↩ ↩
5 Rathmanner & Hutter (2011): "Since Solomonoff provides optimal inductive inference and decision theory solves the problem of choosing optimal actions, they can therefore be combined to produce intelligence. [...] Universal artificial intelligence involves the design of agents like AIXI that are able to learn and act rationally in arbitrary unknown environments. The problem of acting rationally in a known environment has been solved by sequential decision theory using the Bellman equations. Since the unknown environment can be approximated using Solomonoff induction, decision theory can be used to act optimally according to this approximation. The idea is that acting optimally according to an optimal approximation will yield an agent that will perform as well as possible in any environment with no prior knowledge."
Hutter (2005): "Real-world machine learning tasks will with overwhelming majority [sic] be solved by developing algorithms that approximate Kolmogorov complexity or Solomonoff's prior (e.g. MML, MDL, SRM, and more specific ones, like SVM, LZW, neural/Bayes nets with complexity penalty, ...)."
Pankov (2008): "Universal induction solves in principle the problem of choosing a prior to achieve optimal inductive inference. The AIXI theory, which combines control theory and universal induction, solves in principle the problem of optimal behavior of an intelligent agent. A practically most important and very challenging problem is to find a computationally efficient (if not optimal) approximation for the optimal but incomputable AIXI theory. [...] The real value of the AIXI theory is that it provides a prescription for optimal (fastest in the number of agent's observations and actions) way of learning and exploiting the environment. This is analogous to how Solomonoff induction (which, like AIXI, is incomputable), gives a prescription for optimal (fastest in the number of observations) inductive inference. We, therefore, believe that any reasonable computational model of intelligence must recover the AIXI model in the limit of infinite computational resources." ↩
6 Veness, Ng, Hutter, Uther & Silver (2011): "As the AIXI agent is only asymptotically computable, it is by no means an algorithmic solution to the general reinforcement learning problem. Rather it is best understood as a Bayesian optimality notion for decision making in general unknown environments. As such, its role in general AI research should be viewed in, for example, the same way the minimax and empirical risk minimisation principles are viewed in decision theory and statistical machine learning research. These principles define what is optimal behaviour if computational complexity is not an issue, and can provide theoretical guidance in the design of practical algorithms." ↩
7 Hutter (2012): "AIXI is an agent that interacts with an environment in cycles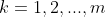 . In cycle
. In cycle  , AIXI takes action
, AIXI takes action 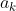 (e.g. a limb movement) based on past perceptions
(e.g. a limb movement) based on past perceptions 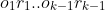 as defined below. Thereafter, the environment provides a (regular) observation
as defined below. Thereafter, the environment provides a (regular) observation 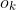 (e.g. a camera image) to AIXI and a real-valued reward
(e.g. a camera image) to AIXI and a real-valued reward 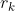 . [...] Then the next cycle
. [...] Then the next cycle 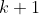 starts. [... T]he simplest version of AIXI is defined by
starts. [... T]he simplest version of AIXI is defined by
"The expression shows that AIXI tries to maximize its future reward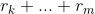 . If the environment is modeled by a deterministic program
. If the environment is modeled by a deterministic program 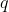 , then the future perceptions
, then the future perceptions 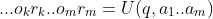 can be computed, where
can be computed, where 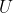 is a universal (monotone Turing) machine executing
is a universal (monotone Turing) machine executing 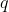 given
given 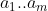 . Since
. Since 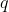 is unknown, AIXI has to maximize its expected reward, i.e. average
is unknown, AIXI has to maximize its expected reward, i.e. average  over all possible future perceptions created by all possible environments
over all possible future perceptions created by all possible environments 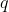 that are consistent with past perceptions. The simpler an environment, the higher is its a-priori contribution
that are consistent with past perceptions. The simpler an environment, the higher is its a-priori contribution 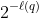 , where simplicity is measured by the length
, where simplicity is measured by the length 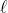 of program
of program 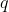 ." ↩
." ↩
8 See Hay (2007). ↩
9 Hutter (2005): "The construction of and the enumerability of
and the enumerability of 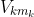 ensure arbitrary close approximations of
ensure arbitrary close approximations of 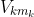 , hence we expect that the behavior of
, hence we expect that the behavior of  converges to the behavior of AIXI in the limit
converges to the behavior of AIXI in the limit  , in some sense." ↩
, in some sense." ↩
10 The concept of wireheading comes from a 1950s experiment in which it was discovered that direct electrical stimulation of mice's brains could strongly reinforce associated behaviors. Larry Niven introduced the term 'wireheading' for a fictional form of brain stimulation reinforcement that acts like intense drug addiction in humans. Niven-style ('irrational') wireheaders self-stimulate due to a lack of self-control; they become short-term pleasure addicts while losing sight of the more complex goals they would like to pursue.
This is in stark contrast to AGIs with simple preferences like AIXI. These 'rational' wireheaders can fully optimize for their goals by seizing control of a simple external reward button or internal reward circuit. So it may be useful to use separate terms for these two problems, like 'pleasure addiction' or 'pathological hedonism' for the human case, 'preference solipsism' for the case of agents without complex eternal goals. ↩
11 Alex Mennen has proposed a variant of AIXI that has preferences over patterns in the environmental Turing machine's framework. This is the Cartesian equivalent of caring about environmental states in their own right, not just about one's input tape. This would mean deviating somewhat from the AIXI framework, but retaining Solomonoff induction as a foundation, and I'd expect this to make the wireheading problem more tractable.
Compare Ring & Orseau's (2011) variant on the problem: "We consider four different kinds of agents: reinforcement-learning, goal-seeking, prediction-seeking, and knowledge-seeking agents[,...] each variations of a single agent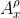 , which is based on AIXI[....] While defining a utility function, we must be very careful to prevent the agent from finding a shortcut to achieve high utility. For example, it is not sufficient to tell a robot to move forward and to avoid obstacles, as it will soon understand that turning in circles is an optimal behavior. We consider the possibility that the agent in the real world has a great deal of (local) control over its surrounding environment. This means that it can modify its surrounding information, especially its input information. Here we consider the (likely) event that an intelligent agent will find a short-cut, or rather, a short-circuit, providing it with high utility values unintended by the agent’s designers. We model this circumstance with a hypothetical object we call the delusion box. The delusion box is any mechanism that allows the agent to directly modify its inputs from the environment. [...] Of the four learning agents, only [the knowledge-seeking agent]
, which is based on AIXI[....] While defining a utility function, we must be very careful to prevent the agent from finding a shortcut to achieve high utility. For example, it is not sufficient to tell a robot to move forward and to avoid obstacles, as it will soon understand that turning in circles is an optimal behavior. We consider the possibility that the agent in the real world has a great deal of (local) control over its surrounding environment. This means that it can modify its surrounding information, especially its input information. Here we consider the (likely) event that an intelligent agent will find a short-cut, or rather, a short-circuit, providing it with high utility values unintended by the agent’s designers. We model this circumstance with a hypothetical object we call the delusion box. The delusion box is any mechanism that allows the agent to directly modify its inputs from the environment. [...] Of the four learning agents, only [the knowledge-seeking agent] 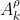 will not constantly use the delusion box. The remaining agents use the delusion box and (trivially) maximize their utility functions. The policy an agent finds using a real-world DB will likely not be that planned by its designers. From the agent’s perspective, there is absolutely nothing wrong with this, but as a result, the agent probably fails to perform the desired task. [...] These arguments show that all agents other than [the knowledge-seeking agent]
will not constantly use the delusion box. The remaining agents use the delusion box and (trivially) maximize their utility functions. The policy an agent finds using a real-world DB will likely not be that planned by its designers. From the agent’s perspective, there is absolutely nothing wrong with this, but as a result, the agent probably fails to perform the desired task. [...] These arguments show that all agents other than [the knowledge-seeking agent]  are not inherently interested in the environment, but only in some inner value." ↩ ↩
are not inherently interested in the environment, but only in some inner value." ↩ ↩
12 A hypothetical naïve monist that made errors analogous to TALE-SPIN's would lack bridging hypotheses, instead treating its software and hardware as separate pieces of furniture in the world. A Cartesian dualist like AIXI lacks bridging hypotheses and instead treats its software and hardware as separate pieces of furniture partitioned into two very different worlds. ↩
References
∙ Hay (2007). Universal semimeasures: An introduction. CDMTCS Research Report Series, 300.
∙ Hutter (2001). Convergence and error bounds for universal prediction of nonbinary sequences. Lecture notes in artificial intelligence, Proc. 12th European Conf. on Machine Learning: 239-250.
∙ Hutter (2005). Universal Artificial Intelligence: Sequence Decisions Based on Algorithmic Probability. Springer.
∙ Hutter (2007). Universal Algorithmic Intelligence: A mathematical top→down approach. In Goertzel & Pennachin (eds.), Artificial General Intelligence (pp. 227-290). Springer.
∙ Hutter (2012). One decade of Universal Artificial Intelligence. Theoretical Foundations of Artificial General Intelligence, 4: 67-88.
∙ Hutter, Legg & Vitanyi (2007). Algorithmic probability. Scholarpedia, 2: 2572.
∙ Orseau (2010). Optimality issues of universal greedy agents with static priors. Lecture Notes in Computer Science, 6331: 345-359.
∙ Pankov (2008). A computational approximation to the AIXI model. Proceedings of the 2008 Conference on Artificial General Intelligence: 256-267.
∙ Rathmanner & Hutter (2011). A philosophical treatise of universal induction. Entropy, 13: 1076-1131.
∙ Ring & Orseau (2011). Delusion, survival, and intelligent agents. Lecture Notes in Computer Science, 6830: 11-20.
∙ Solomonoff (1997). The discovery of algorithmic probability. Journal of Computer and System Sciences, 55: 73-88.
∙ Sunehag & Hutter (2013). Principles of Solomonoff induction and AIXI. Lecture Notes in Computer Science, 7070: 386-398.
∙ Veness, Ng, Hutter, Uther & Silver (2011). A Monte-Carlo AIXI approximation. Journal of Artificial Intelligence Research, 40: 95-142.