Let the wonder never fade!
Aspiring alignment researcher with a keen interest in agent foundations. Studying math, physics, theoretical CS (Harvard 2027). Contact me via Discord: dalcy_me, email: dalcy.mail@gmail.com. They / Them, He / Him.
Posts
Wiki Contributions
Comments
re: second diagram in the "Bayesian Belief States For A Hidden Markov Model" section, shouldn't the transition probabilities for the top left model be 85/7.5/7.5 instead of 90/5/5?
What is the shape predicted by compmech under a generation setting, and do you expect it instead of the fractal shape to show up under, say, a GAN loss? If so, and if their shapes are sufficiently distinct from the controls that are run to make sure the fractals aren't just a visualization artifact, that would be further evidence in favor of the applicability of compmech in this setup.
If after all that it still sounds completely wack, check the date. Anything from before like 2003 or so is me as a kid, where "kid" is defined as "didn't find out about heuristics and biases yet", and sure at that age I was young enough to proclaim AI timelines or whatevs.
btw there's no input box for the "How much would you pay for each of these?" question.
although I've practiced opening those emotional channels a bit, so this is a less uncommon experience for me than for most
i'm curious, what did you do to open those emotional channels?
Out of the set of all possible variables one might use to describe a system, most of them cannot be used on their own to reliably predict forward time evolution because they depend on the many other variables in a non-Markovian way. But hydro variables have closed equations of motion, which can be deterministic or stochastic but at the least are Markovian.
This idea sounds very similar to this—it definitely seems extendable beyond the context of physics:
We argue that they are both; more specifically, that the set of macrostates forms the unique maximal partition of phase space which 1) is consistent with our observations (a subjective fact about our ability to observe the system) and 2) obeys a Markov process (an objective fact about the system's dynamics).
I don't see any feasible way that gene editing or 'mind uploading' could work within the next few decades. Gene editing for intelligence seems unfeasible because human intelligence is a massively polygenic trait, influenced by thousands to tens of thousands of quantitative trait loci.
I think the authors in the post referenced above agree with this premise and still consider human intelligence augmentation via polygenic editing to be feasible within the next few decades! I think their technical claims hold up, so personally I'd be very excited to see MIRI pivot towards supporting their general direction. I'd be interested to hear your opinions on their post.
I am curious as to how often the asymptotic results proven using features of the problem that seem basically practically-irrelevant become relevant in practice.
Like, I understand that there are many asymptotic results (e.g., free energy principle in SLT) that are useful in practice, but i feel like there's something sus about similar results from information theory or complexity theory where the way in which they prove certain bounds (or inclusion relationship, for complexity theory) seem totally detached from practicality?
- joint source coding theorem is often stated as why we can consider the problem of compression and redundancy separately, but when you actually look at the proof it only talks about possibility (which is proven in terms of insanely long codes) and thus not-at-all trivial that this equivalence is something that holds in the context of practical code-engineering
- complexity theory talks about stuff like quantifying some property over all possible boolean circuits of a given size which seems to me considering a feature of the problem just so utterly irrelevant to real programs that I'm suspicious it can say meaningful things about stuff we see in practice
- as an aside, does the P vs NP distinction even matter in practice? we just ... seem to have very good approximation to NP problems by algorithms that take into account the structures specific to the problem and domains where we want things to be fast; and as long as complexity methods doesn't take into account those fine structures that are specific to a problem, i don't see how it would characterize such well-approximated problems using complexity classes.
- Wigderson's book had a short section on average complexity which I hoped would be this kind of a result, and I'm unimpressed (the problem doesn't sound easier - now how do you specify the natural distribution??)
Found an example in the wild with Mutual information! These equivalent definitions of Mutual Information undergo concept splintering as you go beyond just 2 variables:
- interpretation: common information
- ... become co-information, the central atom of your I-diagram
- interpretation: relative entropy b/w joint and product of margin
- ... become total-correlation
- interpretation: relative entropy b/w joint and product of margin
- interpretation: joint entropy minus all unshared info
- ... become bound information
- interpretation: joint entropy minus all unshared info
... each with different properties (eg co-information is a bit too sensitive because just a single pair being independent reduces the whole thing to 0, total-correlation seems to overcount a bit, etc) and so with different uses (eg bound information is interesting for time-series).
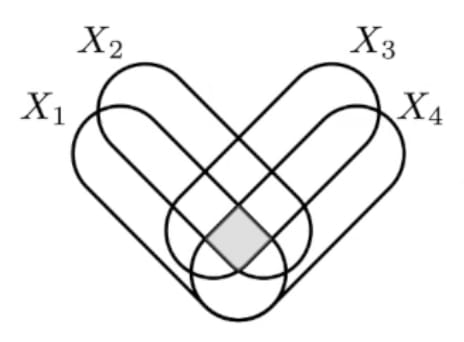
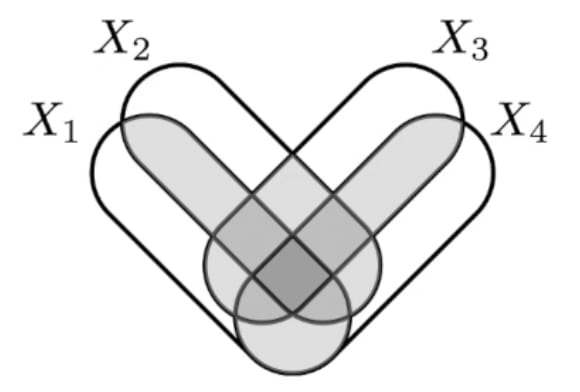
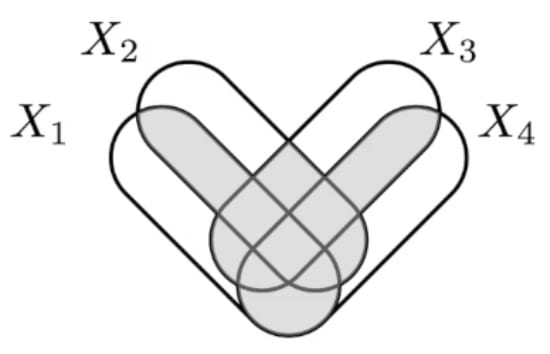
Thoughtdump on why I'm interested in computational mechanics: