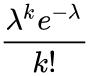If you have the option, it is much better to learn mathematical formulae, theorems, etc., by understanding them rather than by rote memorization. The visualization techniques you describe seem to be intended as ways to make rote memorization easier.

If you have the option, it is also much better to learn mathematical formulae, theorems, etc., by connecting them with other bits of mathematics you know. This is not the same thing as understanding them, but there's some connection between the two.

(You might not have the option. You might find whatever it is very hard to make any sense of, but need to learn it in a hurry for an examination or something. That's a bad situation to be in, and if you aren't in that situation yet you should probably try to avoid it, but that isn't always possible.)

So, for instance, one thing that jumps out at me when I look at the formula for the Poisson distribution is: ${\lambda }^k/k!$ is one term in the series for $e^{\lambda }$ and the other factor, of $e^{-\lambda }$, is what you need to make those terms add up to 1 instead of $e^{\lambda }$. (I am fairly sure this is in fact how I remember the formula for the Poisson distribution.)

That's a connection with other things but doesn't in itself convey any understanding: it doesn't give us a way of working out what the formula is if we happen to forget some detail. But suppose we look at the series for $e^{\lambda t}$ instead of that for just $e^{\lambda }$; then the coefficient of $t^k$ is (aside from that factor of $e^{-\lambda }$) exactly the probability of getting $k$ events; in other words, the formula says that $e^{\lambda (t-1)}$ is the generating function for those probabilities. (The "-1" comes from that factor of $e^{-\lambda }$.)

Now, that's the same thing as saying that $e^{\lambda (t-1)}$ is equal to the expectation of $t^X$ where $X$ is Poisson-distributed with rate $\lambda$. (If it isn't obvious why, try writing down what that expectation is as a sum of probabilities times values.) Perhaps that's obvious if you look at it the right way? Well, saying that $X$ is Poisson-distributed with rate $\lambda$ means that it's the limit for large $N$ of what you get by having $N$ opportunities for events to happen, each independently with probability $\lambda /N$. So $t^X$ is (the limit of) the product of $N$ independent things that are either $t$ (with probability $\lambda /N$) or 1 (otherwise). The expectation of a product of independent things is the product of their expectations. The expectation of one of those things is $1+(t-1)\frac{\lambda }{N}$. So we're looking at the limit of ${(1+(t-1\left)\frac{\lambda }{N}\right)}^N$, and that sort of limit is famously one way of defining $e^{\text{whatever}}$. So we also have an (admittedly slightly clumsy) way of seeing why the formula has to be right.

None of this is an answer to the question you actually asked: how can you visualize this formula, so you can memorize it without any understanding? If you really truly need to do that, then you should ignore everything I just wrote. But if what you need is to be able to remember and use the formula, then I think this sort of thing will be much better for you. Why? Because it scales better. The more things you learn by understanding them and/or by making connections to other bits of mathematics, the easier it is to learn the next thing you need to remember, because you have more tools for understanding and more things to connect to.