Imagine you have a goal of identifying a novel disease by the time some small fraction of the population has been infected. Many of the signs you might use to detect something unusual, however, such as doctor visits or shedding into wastewater, will depend on the number of people currently infected. How do these relate?

Bottom line: if we limit our consideration to the time before anyone has noticed something unusual, where people aren't changing their behavior to avoid the disease, the vast majority of people are still susceptible, and spread is likely approximately exponential, then:

$$\mathrm{incidence}=\mathrm{cumulative\; infections}\frac{\ln \left(2\right)}{\mathrm{doubling\; time}}$$

Let's derive this! We'll call "cumulative infections" $c\left(t\right)$, and "doubling time" $T_d$. So here's cumulative infections at time $t$:

$$c\left(t\right)=2^{\frac{t}{T_d}}$$

The math will be easier with natural exponents, so let's define $k=\frac{\ln \left(2\right)}{T_d}$ and switch our base:

$$e^{kt}$$

Let's call "incidence" $i\left(t\right)$, which will be the derivative of $c\left(t\right)$:

$$i\left(t\right)=\frac{d}{dt}c\left(t\right)=\frac{d}{dt}{e}^{kt}=k{e}^{kt}$$

And so:

$$\frac{i\left(t\right)}{c\left(t\right)}=\frac{k{e}^{kt}}{e^{kt}}=k=\frac{\ln \left(2\right)}{T_d}$$

Which means: $$i\left(t\right)=c\left(t\right)\frac{\ln \left(2\right)}{T_d}$$

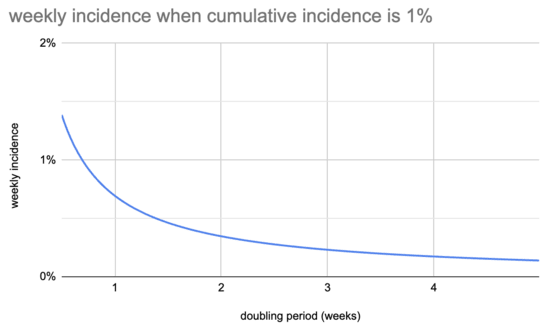
What does this look like? Here's a chart of weekly incidence at the time when cumulative incidence reaches 1%:

For example, if it's doubling weekly then when 1% of people have ever been infected 0.69% of people became infected in the last seven days, representing 69% of people who have ever been infected. If it's doubling every three weeks, then when 1% of people have ever been infected 0.23% of people became infected this week, 23% of cumulative infections.

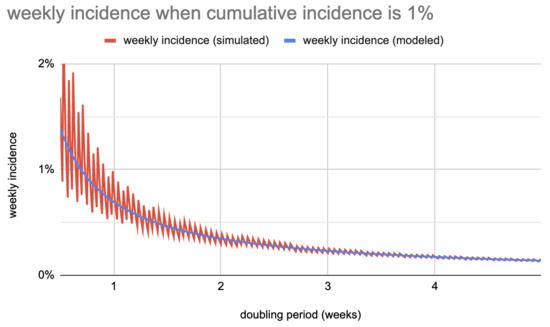
Is this really right, though? Let's check our work with a bit of very simple simulation:

def simulate(doubling_period_weeks):
  cumulative_infection_threshold = 0.01
  initial_weekly_incidence = 0.000000001
  cumulative_infections = 0
  current_weekly_incidence = 0
  week = 0
  while cumulative_infections < \
        cumulative_infection_threshold:
    week += 1
    current_weekly_incidence = \
        initial_weekly_incidence * 2**(
          day/doubling_period_weeks)
    cumulative_infections += \
        current_weekly_incidence

  return current_weekly_incidence

for f in range(50, 500):
  doubling_period_weeks = f / 100
  print(doubling_period_weeks,
        simulate(doubling_period_weeks))

This looks like:

The simulated line is jagged, especially for short doubling periods, but that's not especially meaningful: it comes from running the calculation a week at a time and how some weeks will be just above or just below the (arbitrary) 1% goal.

Comment via: facebook, mastodon