This is a useful paper for those wanting to better understand the risks posed by pandemics and, more generally, global catastrophic biological risk.
I have not seen this paper mentioned on LW or EAF and it does not appear on LW or EAF when entered in the search box, so I thought I'd contribute it to the wider conversation.
In this linkpost, I include, in the following order, the structure of the paper, the paper's abstract, some commentary and quotes, and the 2 most important figures from the paper.
To see the papers that have cited Intensity and frequency of extreme novel epidemics, click here. To see papers that Intensity and frequency of extreme novel epidemics cites, click here.
Possible ways to cite the paper:
Marani, Marco, Gabriel G. Katul, William K. Pan, and Anthony J. Parolari. "Intensity and frequency of extreme novel epidemics." Proceedings of the National Academy of Sciences 118, no. 35 (2021): e2105482118.
@article{marani2021intensity, title={Intensity and frequency of extreme novel epidemics}, author={Marani, Marco and Katul, Gabriel G and Pan, William K and Parolari, Anthony J}, journal={Proceedings of the National Academy of Sciences}, volume={118}, number={35}, pages={e2105482118}, year={2021}, publisher={National Acad Sciences} }
Structure
- Introduction
- Results
- The Probability Distribution of Epidemic Intensity
- The Probability of Occurrence of Extreme Epidemics
- Discussion
- Materials and Methods
Abstract
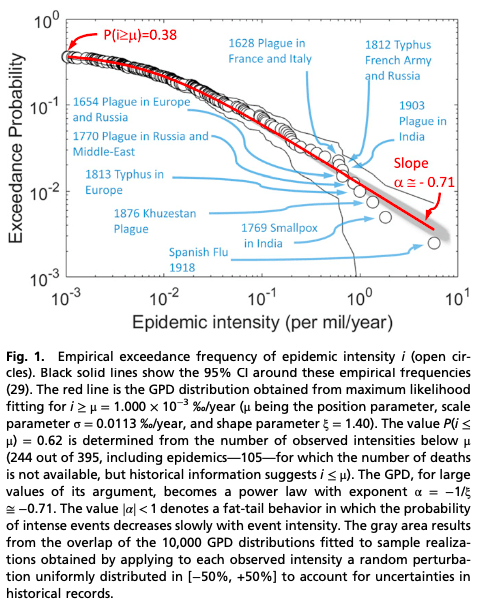
Observational knowledge of the epidemic intensity, defined as the number of deaths divided by global population and epidemic duration, and of the rate of emergence of infectious disease outbreaks is necessary to test theory and models and to inform public health risk assessment by quantifying the probability of extreme pandemics such as COVID-19. Despite its significance, assembling and analyzing a comprehensive global historical record spanning a variety of diseases remains an unexplored task. A global dataset of historical epidemics from 1600 to present is here compiled and examined using novel statistical methods to estimate the yearly probability of occurrence of extreme epidemics. Historical observations covering four orders of magnitude of epidemic intensity follow a common probability distribution with a slowly decaying power-law tail (generalized Pareto distribution, asymptotic exponent = −0.71). The yearly number of epidemics varies ninefold and shows systematic trends. Yearly occurrence probabilities of extreme epidemics, Py, vary widely: Py of an event with the intensity of the “Spanish influenza” (1918 to 1920) varies between 0.27 and 1.9% from 1600 to present, while its mean recurrence time today is 400 y (95% CI: 332 to 489 y). The slow decay of probability with epidemic intensity implies that extreme epidemics are relatively likely, a property previously undetected due to short observational records and stationary analysis methods. Using recent estimates of the rate of increase in disease emergence from zoonotic reservoirs associated with environmental change, we estimate that the yearly probability of occurrence of extreme epidemics can increase up to threefold in the coming decades.
Commentary and Quotes
- Main contributions: produced a dataset of yearly historical epidemics [1600, 2022]; estimated annual probability of occurrence of extreme epidemics; commented on how the annual probability of extreme epidemics may change
- Dataset (see here): "...the 1600 to 1945 dataset includes 182 epidemics with known oc- currence, duration, and number of deaths, 108 known to have caused less than 10,000 deaths, and 105 for which only occurrence and duration are recorded, for a total of 395 epidemics."
- Epidemic intensity "..is well described by a generalized Pareto distribution (GDP)"
- Recurrence of Spanish Flu-like pandemic: "Such a change would bring, possibly over decadal time scales, the average recurrence interval of a Spanish flu–like event down to 127 y (95% CI 115 to 141 y), comparable to the value it had around 1918 (i.e., 91 y)."
- Recurrence of COVID-19 like pandemic: "Our analysis also quantifies how frequently a COVID-19–like event may occur in the future. Current information (19) indicates that the epidemic progresses at a rate of about 2.5 million deaths/ year (3,549,710 in 72 wk), which, normalized by the global pop- ulation, corresponds to an intensity of the epidemic of 0.33 ‰/year. Using the number of epidemic occurrences observed in the past 20 y (i.e., 2000 to 2019) in the MEVD model, this in- tensity corresponds to an average recurrence time of 59 y (95% CI 55 to 64 y)."
Dataset Figure
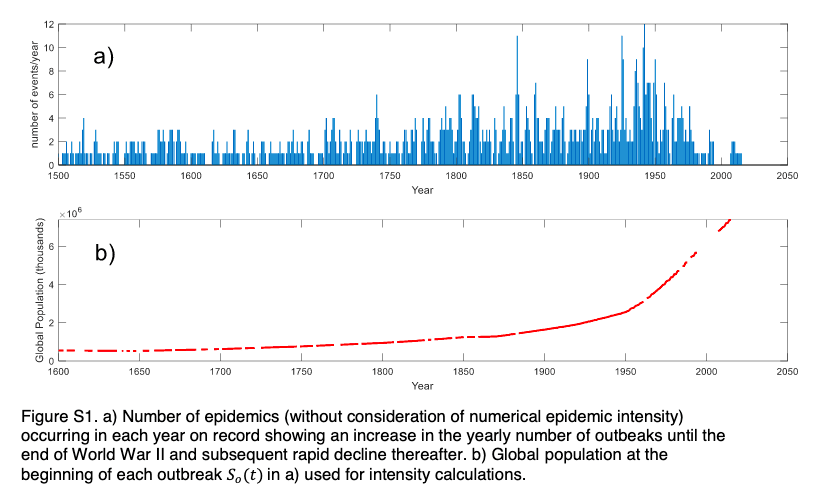
Estimates Figure