(Jointly written by Astra Kolomatskaia and Mike Shulman)

This is part one of a three-part series of expository posts on our paper Displayed Type Theory and Semi-Simplicial Types. In this part, we motivate the problem of constructing SSTs and recap its history.

A Prospectus

 There are different ways to describe the relationship between type theory and set theory, but one analogy views set theory as like machine code on a specific CPU architecture, and type theory as like a high level programming language. From this perspective, set theory has its place as a foundation because almost any structure that one thinks about can be encoded through a series of representation choices. However, since the underlying reasoning of set theory is untyped, it can violate the principle of equivalence. Thus, for example,  there is no guarantee that theorems proved in set theory about groups automatically translate to theorems about group objects internal to a category.

 Within the programming language analogy, one can fully define a high level programming language and its operational semantics without specifying any particular compiler or any concept of a CPU architecture. Similarly, type theory allows one to reason with concepts defined in a purely operational, as opposed to representational, manner. The goal of type theory is to create expressive and semantically general languages for reasoning about mathematics.

 Homotopy Type Theory (HoTT) is a perspective on intensional dependent type theory which regards types as homotopical spaces. In HoTT, one is only allowed to speak of concepts "up to homotopy". This feature allows one to interpret HoTT into any $\infty$-topos. This is a fascinating state of affairs, because, in general, the constructions of higher category theory, among all those in mathematics, are the ones that sit least comfortably in a set-theoretic foundation.  Thus, much of the excitement about HoTT has involved its promise to provide a language capable of reasoning about higher structures.

 So far, however, the type theories used for HoTT have been limited in the generality of the higher structures they can discuss.  With types as homotopical spaces, structures defined using a finite number of these and maps between them can be represented.  For instance, the language of HoTT has been great for formulating $1$-category theory, and there exist large formalised libraries such as the 1lab with such results; and a lot of abstract homotopy theory turns out to be doable in this way as well, sometimes by using wild categories.  But $1$-categories and wild categories have only two layers of structure, objects and morphisms, while we would hope also to reason internally about structures that have infinite towers of layered structure, such as $\infty$-categories.  However, such structures have thus far resisted all attempts at definition!

 One simple case of such an infinitary structure is a semi-simplicial type (SST). This is particularly important because many notions of classical higher category theory are traditionally formulated using simplicial or semi-simplicial objects.  Thus, if we had a tractable approach to SSTs in HoTT, we could expect that many, if not all, other infinitary structures could also be encoded.  This is one reason that the problem of defining SSTs, which was originally proposed by Vladimir Voevodsky over a decade ago, has become one of the most important open problems in Homotopy Type Theory.

SSTs: The Fibred Perspective

 To explain the problem of defining SSTs, we start with a classical perspective grounded first in set theory and later in homotopy theory. A semi-simplicial set is defined to consist of sets $X_n$ for $n\ge 0$, along with face maps ${\partial }_k:X_n\to X_{n-1}$, for $k\in \{0,\dots ,n\}$, satisfying the relations: 

 One thinks of $X_n$ as the set of $n$-simplices, and of the face maps as giving the boundary components of a given $n$-simplex. For example, $X_0$ is the set of points, $X_1$ is the set of lines, and $X_2$ is the set of triangles. A triangle has three boundary lines which share three boundary points in common.

 The problem of constructing semi-simplicial types can intuitively be thought of as the problem of constructing semi-simplicial sets but with homotopy types replacing sets. Here, the key is that the semi-simplicial identities from before would now read: 

 Thus, we have replaced the strict set-theoretic notion of equality with a homotopical proof relevant form of equality, meaning that the choice of ${\alpha }_{k,l}$ now carries data. In order for this notion to give something useful, we must impose coherences on these data. At the first level, for $k<l<m$, we can prove that ${\partial }_k\circ {\partial }_l\circ {\partial }_m\simeq {\partial }_{m-2}\circ {\partial }_{l-1}\circ {\partial }_k$ in two different ways, and we would like for those proofs to themselves be equal. This requires providing coherences ${\beta }_{k,l,m}$ such that: 

 Which we can visualise by the following diagram:

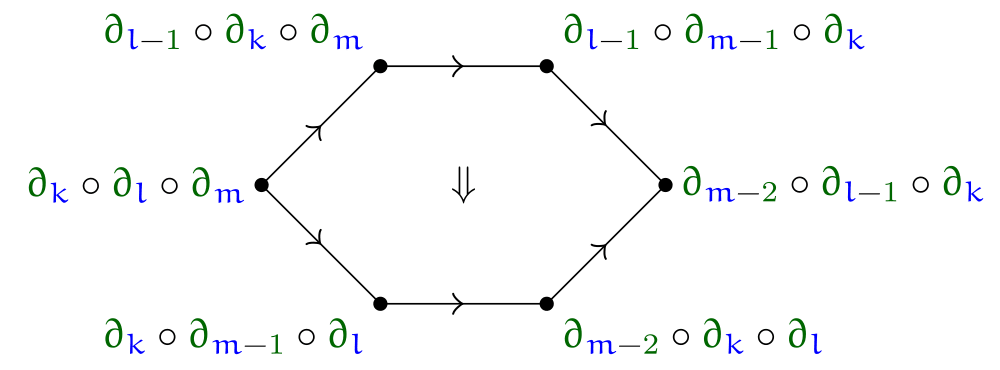
 Of course, now the ${\beta }_{k,l,m}$ themselves carry data, and we have to impose coherences on those. These identities come up in the context of quadruples of deletions. The first identity is given by a square diagram that says that the ${\alpha }_{k,l}$ homotopies applied to non-interacting indices commute. The second identity is given one dimension up, and describes a filler for the following figure, called a permutohedron, whose faces are the previously mentioned hexagons and squares. It can be visualised via the illustration by Tilman Piesk:

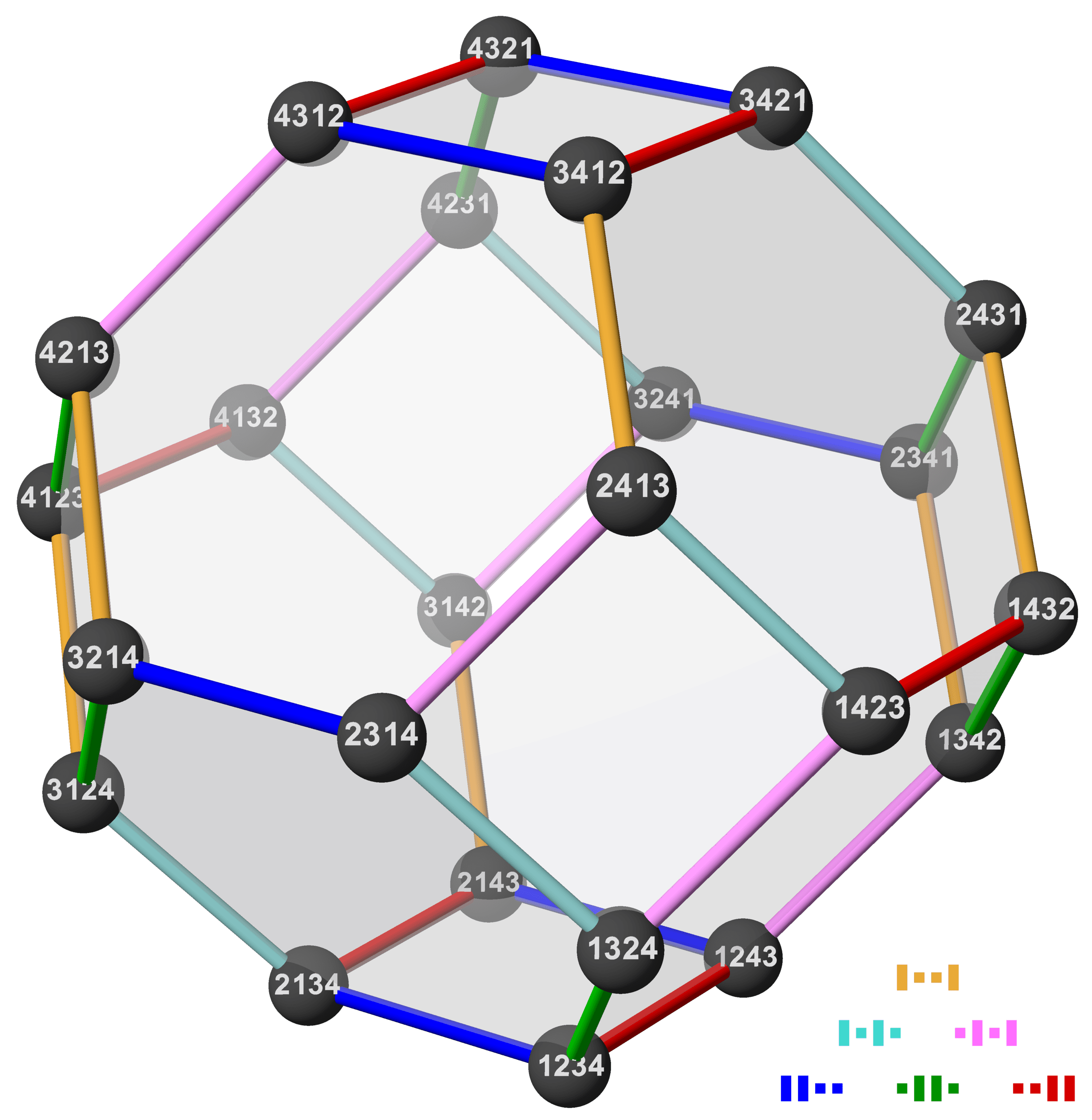
 Writing down a formula for this is complicated, and things only become worse when you consider sequences of five or more deletions! We have thus run into the fundamental obstacle to defining infinitary structures – this goes by the technical name of Higher Coherence Issues.

SSTs: The Indexed Perspective

 The previous section demonstrates a general phenomenon related to infinitary structures: as soon as the symbol $(=)$ gets used in the definition, one is plunged into also constraining the values of this data carrying equality by way of an infinite tower of coherences, each depending on the definitions of all prior ones and growing in complexity as the dimensions increase.

 One promising approach, then, would be to try and define higher structures without reference to equality. In the case of semi-simplicial types, one can think of an intuitive definition which promises to do so, by breaking up "the set of $n$-simplices" into a family of sets indexed by their boundaries. For example, we split up the total space of lines into many separate spaces of lines, each joining two definite endpoints (although the dependence of these indexed spaces on the endpoints is continuous). This is analogous to the two basic ways to define a category, with one collection of morphisms or with a family of collections of morphisms.

 Roughly, then, in this approach a semi-simplicial type is an "infinite record type" whose fields specify notions of points, lines, triangles, etc. When comparing this to the notion from the previous section, we call the previous one fibred and this one indexed. The face maps of the fibred formulation simply become index lookups in the indexed formulation, and this non-data is automatically infinitely coherent.

 Of course, this is not yet precise either: there is the problem of what the ellipsis represents, and the lack of notion of an infinite record type. But there is evidently some kind of pattern, so it seems intuitive that this direction would be more promising as an approach to defining SSTs in type theory.

Equivalence of the Indexed and Fibred Formulations

 We can begin to argue that the truncated forms of the indexed and fibred definitions are equivalent, when all coherences are included in the latter, by considering the truncated cases that only go up to $n$-simplices for some finite $n$. For example, suppose that we are given the data ${\partial }_0,{\partial }_1:X_1\to X_0$, and ${\partial }_0,{\partial }_1,{\partial }_2:X_2\to X_1$. We would like to use this data to define indexed types. At the first two stages, we define:

For the next stage, we are defining ${\tilde{X}}_2(x,y,z,(\alpha ,p_0,q_0),(\beta ,p_1,q_1),(\gamma ,p_2,q_2))$.

 One may be tempted to say that this consists of $f:X_2$ with boundary data $\alpha ,\beta ,\gamma$, by asserting, for example, that ${\partial }_{2}f=\alpha$. However this equality in $X_1$ leaves the endpoints free. For example, in the case of the singular semi-simplicial type of a type $X$, so long as the lines ${\partial }_{2}f$ and $\alpha$ lived in the same connected component of $X$, they could be identified by this criterion. We see, then, that this comparison should be performed in the type ${\tilde{X}}_1(x,y)$.

 In order to create an element of ${\tilde{X}}_1(x,z)$, we want to use ${\partial }_{1}f$. We then have that $r_2:{\partial }_0{\partial }_{1}f=z$, giving us a proof that the right endpoint is $z$. However, for the left endpoint, we only have $r_0:{\partial }_1{\partial }_{2}f=x$, and we need to concatenate this on the left with an equality ${\partial }_1{\partial }_{1}f={\partial }_1{\partial }_{2}f$ in order to show that ${\partial }_1{\partial }_{1}f=x$, as required. A similar analysis applies for ${\tilde{X}}_1(y,z)$. Thus we require the commutation identities: 

Provided these identities as part of our starting data, we would then complete the definition as follows:

 Using contractible singletons and path algebra, one can show that forming the total spaces of the resulting indexed types leads to types equivalent to $X_0,X_1,X_2$. Similarly, starting off with indexed types ${\tilde{X}}_0,{\tilde{X}}_1,{\tilde{X}}_2$, forming their total spaces, and then performing the above construction results in equivalent types. This demonstrates an equivalence between the indexed and fibred definitions up to the second stage.

The Essence of the Problem

 One can continue the above analysis to the third stage, although writing out the details would be exceptionally painful. But we can at least extrapolate the way in which the higher coherences would play a role in the definition. This leads us to two conclusions. Firstly, that the higher coherences are necessary in the fibred formulation, if we would like to extract indexed simplex types from it (which we undoubtedly would). And secondly, that since the indexed perspective is equivalent to the fibred perspective, solving the problem of defining indexed SSTs in type theory would be tantamount to solving the coherence issues in the fibred perspective; thus we should expect this problem to be more difficult than it seems.

 Indeed, every naive approach to defining SSTs through the indexed formulation seems to run into the same kinds of higher coherence issues. Almost without exception, whatever clever scheme one comes up with for formalising the pattern, it eventually transpires that in order to complete the construction, one needs to simultaneously prove a lemma about the construction. And then in order to complete that lemma, one needs to prove a meta-lemma about the proof of the lemma. In order to prove the meta-lemma, one needs to prove a meta-meta-lemma about the proof of the meta-lemma. And so on...

 It's difficult to give any more details in general. It seems that to truly appreciate this, one almost has to come up with one's own idea for defining SSTs and try to implement it in of a proof assistant. From the outside, it seems that there's an obvious pattern to the structure of the $n$-simplex types, so one doesn't expect it to be so hard going in. And the infinite regress tends to pop up in surprising places, when proving lemmas that seem so obvious that one tends to leave them for last (or neglect to write them down at all on paper), assuming their proofs will be easy.

Autophagy

 The problem of semi-simplicial types, and higher coherence more generally, is also closely connected to the problem of autophagy, or "HoTT eating itself". In fact both of us ran into this connection independently, Mike in a blogpost from almost exactly ten years ago, and Astra in a second attempt to understand why the problem was hard.

 The idea is that since the pattern in the indexed $n$-simplex types can be defined syntactically, if we could define the syntax and typing rules of HoTT inside of HoTT, and write a self-interpreter that takes an internally-defined well-typed type or term and returns an actual type or term, then we could define the $n$-simplex types syntactically and then apply the self-interpreter. However, in the course of trying to write a self-interpreter, one encounters essentially the same permutahedral identities described above. Not every approach to constructing SSTs has to go through syntax, of course, but this suggests that the problem of SSTs is closely related to the problem of self-interpreters and a notion of infinitely-coherent syntax for type theories. Indeed, one may hope that perhaps solving SSTs would be sufficient to enable self-interpretation, as we hope it would be for other higher coherence problems.

We now discuss two alternative approaches to solving this related collection of problems:

The Two-Level Approach

 As noted above, in classical homotopy theory, it is possible to define (fibred) semi-simplicial types without needing infinite coherences, by using the ambient strict set-theoretic notion of equality. Thus, one way to avoid the problem of infinite coherences in HoTT is to re-introduce a stricter notion of equality. Two-level type theory (2LTT), formulated by Annenkov, Capriotti, Kraus, and Sattler, following an idea of Voevodsky, achieves this by stratifying types into "inner" or "fibrant" types, which are homotopical, and "outer" or "non-fibrant exo-types", which are not. The non-fibrant equality exo-type then plays the role of the strict set-level equality in classical homotopy theory, enabling a correct definition of semi-simplicial types without incorporating higher coherences... under an additional hypothesis.

 Specifically, in two-level type theory there is both a fibrant natural numbers type ("nat") and a non-fibrant natural numbers exo-type ("exo-nat"). Without additional assumptions on the relation between these two, all we can define (apparently) is the family of types of $n$-truncated semi-simplicial types indexed by $n$ in exo-nat. The "limit" of these types can be easily constructed, but without further assumptions it is only be an exo-type, not a fibrant type.

 A sufficient assumption for this is that the two kinds of natural numbers coincide, or equivalently that exo-nat is fibrant. This appears a fairly strong axiom, however; it holds in the "classical" simplicial model, but it is unknown whether all $(\infty ,1)$-toposes can be presented by a model in which it holds. A better axiom, therefore, is that exo-nat is "cofibrant", a technical term from 2LTT essentially saying that $\Pi$-types with it as their domain preserve fibrancy, and therefore in particular the limit of a tower of fibrant types is fibrant. Elif Uskuplu has recently shown that any model of type theory whose types are closed under externally indexed countable products (including models for all $(\infty ,1)$-toposes) can be enhanced to a model of 2LTT in which exo-nat is cofibrant.

 Thus, this approach has reasonable semantic generality. However, it is unclear how practical it is for formalization in proof assistants. Paper proofs in 2LTT often assume that the exo-equality satisfies the "reflection rule" and hence coincides with definitional equality. But this is very difficult to achieve in a proof assistant, so implementations of 2LTT (such as Agda's recent two-level flag) usually instead assume merely that the exo-equality satisfies Uniqueness of Identity Proofs. Unfortunately, this means we have to transport across exo-equalities explicitly in terms, which tends to lead to large combinatorial blowups in proofs.

 Informally, one can argue that 2LTT is a "brute force" solution: we internalize the entire metatheory (the universe of exo-types), and then assume that whatever infinite constructions we want (e.g. exo-nat-indexed products) can be reflected into the original type theory. We would like a solution that is more closely tailored to our goal, allowing more external equalities to be represented definitionally in the syntax.

The Synthetic Approach

 Another approach is to give up on the goal of defining (semi-)simplicial types and instead axiomatize their behavior. This is analogous to how ordinary homotopy type theory axiomatizes the behavior of $\infty$-groupoids rather than defining them in terms of sets. In type theory we call this a "synthetic" approach, in contrast to the "analytic" approach of defining them out of sets, making an analogy to the contrast between Euclid's "synthetic geometry" of undefined points and lines and the "analytic geometry" of pairs of real numbers.

 Mike and Emily Riehl formulated a "simplicial type theory" like this in A type theory for synthetic ∞-categories, where the types behave like simplicial objects. Specifically, there is a "directed interval" type that can be used to detect this simplicial structure, analogous to the undirected interval in cubical type theory that detects the homotopical structure. One can then define internally which types are "Segal" and "Rezk" and start to develop "synthetic higher category theory" with these types.

 This sort of synthetic higher category theory is under active investigation, and shows a lot of promise. In particular, there is now a proof assistant called Rzk implementing it, and many of the basic results have been formalized. Many of us regard this theory (and its relatives such as "bicubical" type theory) as the most practical approach to "directed type theory" currently available.

 However, taking a synthetic approach has also undeniably changed the question. For various reasons, it would be interesting and valuable to have a type theory in which we can define (semi-)simplicial types rather than postulating them. This is the problem addressed in our paper, to which we will turn in the second post of this series.