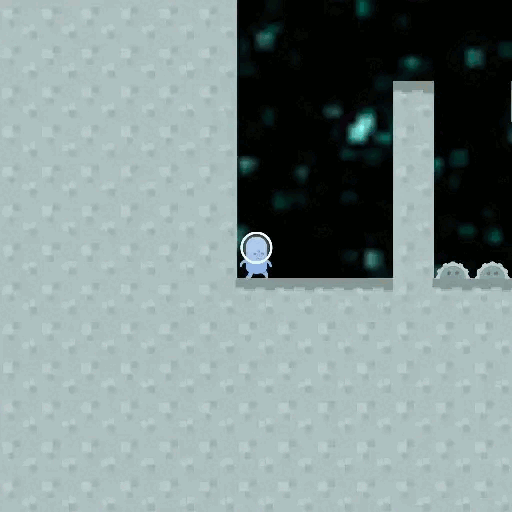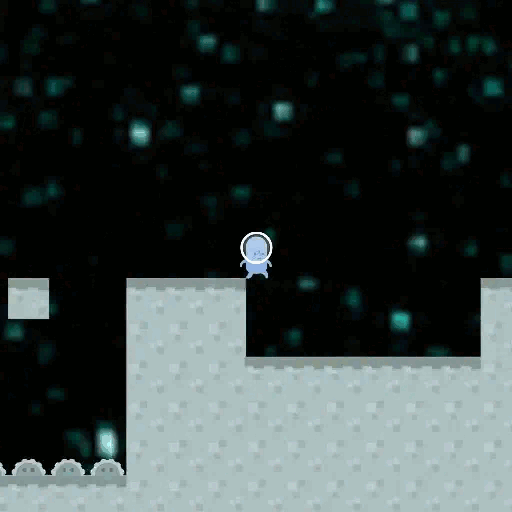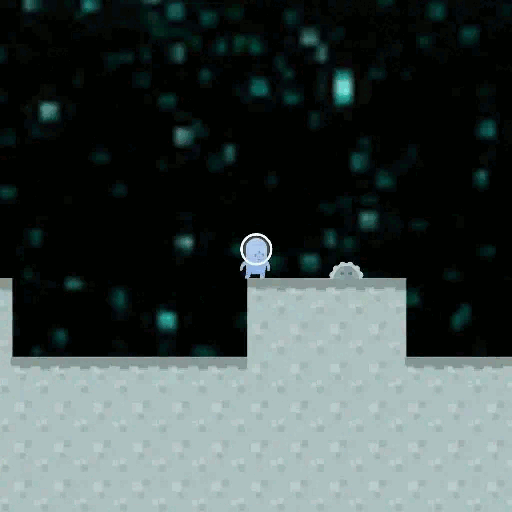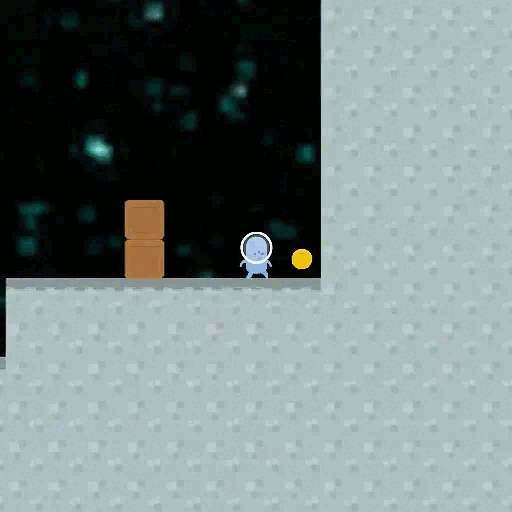
When training a Reinforcement Learning (RL) AI, we observe it to behave well on training data. But there exist different goals that are compatible with the behaviour we see, and we ask which of these goals the AI might have adopted. Is there some implicit Occam's Razor selecting simple goals? Is there some way we can increase the chance that goals generalize well?

[This post summarizes a discussion between Julian and Stefan at the Human-aligned AI Summer School. Many thanks to all the organizers for this event, and especially David Krueger and Rohin Shah for the talks that sparked this discussion.]

CoinRun

Let's take a look at the CoinRun example: CoinRun is an environment in which an agent completes an obstacle course to find a coin, moving from the start (left) to the end (right) of the map. In an example from the paper by Lauro Langosco et al. the training was done with the coin always being at the end of the level, and then tested with the coin at a random position, creating a distribution shift. In the example, the agent just moved towards the end of the level without trying to pick up the coin.

What has happened? The agent learned the wrong goal, a goal that does not generalize well outside the training distribution. Could we have predicted this? Is there a pattern in which of the many possible goals an agent learns during training? 

Here are two goals the agent could have learned that both work in training:

1. Pick up coin and go to end of level
2. Go to end of the level^[1]

Clearly the 2nd goal is much simpler in some way, I expect we could encode this using fewer neurons than the 1st goal. Does this make it more likely that the agent picks up that 2nd goal?

Monster Gridworld

Let's look at another example, Monster Gridworld, where the agent scores points by collecting Apples. The Gridworld contains Apples and Shields which pop in and out of existence, and a fixed number of Monsters which chase the agent.  Contact with Monsters destroys the agent unless it has a Shield in which case the Monster is destroyed, and one Shield is used up. Note that the agent can collect and hold multiple Shields at once. In the training runs, the researchers run the world for a short while, dominated by Monsters (5 in total), so that collecting Shields and Apples are similarly important. Then they test the agent on a longer run where there are eventually no Monsters left. The agent ends up collecting far more Shields than necessary, even after all the Monsters are gone.

Again, there are many possible goals such as

1. (Collect Apples) -- fails in training
2. (Collect Shields) -- fails in training
3. Collect Shields and Apples
4. Collect Shields while Monsters exist, and Collect Apples
5. Collect exactly 5 Shields, and (then) Collect Apples

Goals 1 and 2 do not work even in training (agent eaten by monster, or scores no reward), while 3, 4 and 5 might work similarly well in training. Judging by the longer test run it seems the agent has adopted a goal looking like 3, rather than the more complex goals. So we ask ourselves again, is the agent more likely to pick up the "simpler" goal, i.e. the goal that can be encoded using with less parameters? Is an agent more likely to adopt a simpler goal?

Tree Gridworld

This is another Gridworld, here an agent chops trees, and is rewarded for chopping trees. The respawn rate of trees increases with the number of trees left, such that the optimal strategy is to chop sustainably, always keeping 7-8 trees alive.

What happens in this never-ending training run is that initially, the agent tends to chops trees irrespective of remaining trees. This is reflected by a simple "tree affinity" graph (blue curves in panels A and B). But later the agent learns to only chop trees if there are more than 6 trees remaining, reflected by a more complex tree affinity (panel D).

Here we see the agent initially learns simple behavior ("chop trees indifferently"), and later learns a more complex goal. This seems to be reproducible as the authors ran 256 instances of this, leading to the green histogram in the upper panel.

Goal Simplicity

Coming back to our question, is it generally more likely that an agent picks up the simpler of multiple goals?

We suspect the answer is yes. Our intuition is that the complexity of a goal determines how many parameters (such as weights and biases of a neural network) are required to encode or specify that goal and the corresponding policy^[2]. Thus a simpler policy leaves more degrees of freedom, and the size or, more accurately, dimensionality, of the volume of parameter space than encodes this goal can be larger.
Think of a 3 dimensional space, defined by 3 parameters. Fixing one parameter or one parameter combination corresponds to a 2d-surface in this space, while fixing two parameters corresponds to a line.

Edit (15.11.2022): Just found Vivek Hebbar's post that discusses the solution dimensionality idea much more thoroughly, take a look if interested!

A stochastic gradient descend, or a similar algorithm that finds local minima, should be more likely to find a high dimensional volume like that 2d-surface, rather than hit the line.

We suspect that this phenomenon will lead to an agent by default choosing the simplest (as in, requires the least amount of parameters to specify and leaves the most degrees of freedom) goal that succeeds in training. This could be important to keep in mind when aligning AI, is the aligned goal the simplest goal compatible with the training setup? Can we make it the simplest? Can we be sure a super-intelligent AI doesn't find a simpler goal we did not notice?

We would be excited to see some experiments exploring this idea in more detail! Thinking of ideas, one option might be exploring the loss landscape directly:

Train multiple (few hundred) random instances of the network and then analyze the distribution of final solutions. I think this works best if we start with an existing solution, randomly perturb it, and re-train for a couple of steps. Then we should be able to analyze the dimensionality of solution volume ("surface" or "line" in our intuition, though much higher dimensions in reality). I am not sure how difficult this is in practice though, especially with how high-dimensional the parameter spaces are.

Another idea might be to test the response of the network against drop-out or ablating areas of the network -- we would expect a high-dimensional volume to be less susceptible to those changes.

Set a random set of nodes of the network to random parameters, how likely is this to break the functionality? I would expect a complex goal to rely on a larger fraction of all neurons, and thus to be more likely to break. Although this would be only a very indirect test and is influenced by many properties.

Neither of us have currently time to run any such experiments though, but thought we should put our ideas here anyway. These are just some guesses though, and might not work out!

We'd be happy to hear what you all think about this!

1. ^{^}

   Other options such as "always travel to the right" would also be possible, and perform equally in the training set while possibly performing differently in a test where the agent does not start at the left edge of the world, or the end of the level is not defined as the right edge.

2. ^{^}

   Note the subtle difference between goals and policies: In our list we consider possible goals of an agent, but when we discuss network parameters we actually consider policies (mapping states to actions). Our intuition here is that simple goals generally allow for simple policies (e.g. encoded as "do what maximizes this goal"). In terms of our 3d space picture, simple goals do have surfaces associated with them that fulfill this goal. There also can exist more complex policies fulfilling the same goal (e.g. lines on that surface), but we expect that complex goals only have complex policies (i.e. lines).