The majority of this work was conducted during the 2.5 day AI Safety x Physics Grand Challenge (2025), run by PIBBSS, Timaeus, & Apart Research. We thank Paul Riechers for suggesting this problem (amongst many good suggestions from him and other mentors during the hackathon). More details can be found in an updated (draft) report.

Summary

Context: Computational mechanics has provided examples for which models of the underlying data generating process can be easily found within a transformer's activations. These examples provide concrete settings in which to understand how transformers build world models and how they utilize these world models to form their outputs.
Problem: We focus on a particular data-generating process, RRXOR, and try to better understand how these world models and their formation are affected by architectural constraints inherent to transformers. This is a first step towards identifying the precise underlying circuitry by which transformers utilize these world models to make next-token predictions for this data process.
Experiment & Results: We trained a small transformer on data generated by the RRXOR process and compare its outputs to an ansatz for constrained belief updating previously suggested for similar data.
- We note that this ansatz seemingly fails to generalize to the RRXOR process.
- Despite this, we empirically study the attention patterns of our transformer, finding preliminary evidence that some of the signatures of constrained belief updating found in the above work are still present, despite no longer being predicted by theory.
Next steps: We expect these results will help in forming a more general predictions for how architectural constraints affect the world models that transformers build. Though we focus on a single data process here, we expect this work to be a useful stepping stone in understanding how transformers build and utilize world models in the large scale transformers trained on natural language that are of interest to safety. We discuss some additional stepping stones in the last section.

Introduction & Motivation

LLMs have become increasingly embedded in everyday life, and yet largely remain black boxes. Fully understanding their output requires knowing whether they are at most capable of producing plausible sounding (but ultimately just stochastically chosen) answers, or if they can develop accurate and legible internal models of the world that produced their training data. A particularly concrete approach to this question was taken up in (Shai et al., 2024), which used the framework of computational mechanics to show that for specific data classes, intricate structures – known as belief state geometries, whose form is dictated by optimal prediction of the data generating process – could be easily identified in a transformer’s residual stream.

While the presence of these belief state geometries suggests that transformers (at least in some cases) build models of underlying data-generation processes, it remains to fully understand these beliefs. In particular:

How and when are these world models formed?
How are these world models dependent on the transformer’s architecture? Conversely, how do underlying information-theoretic properties of the data generation process affect how the world model is represented within the transformer?
By which specific mechanisms are these world models used by the transformer to produce its outputs?

The follow-up work (Piotrowski et al., 2025) focused on (2) and (3) (as we will below), pointing out a seeming tension: while optimal prediction requires recursively updating probability distributions after every new token in a sequence, a transformer’s attention head relies on parallelized mechanisms that process an entire context window of tokens at once. They then showed how this tension could be resolved, studying one example of a data generating process from their considered class. After writing down an ansatz for approximate next token prediction (when constrained to parallel updates), they provided evidence that an initial attention layer implemented this constrained updating and had an approximate belief state geometry associated with it. Later fully connected layers then transformed this constrained/approximate belief state geometry into the exact structure dictated by optimal prediction, as depicted in the figure below.

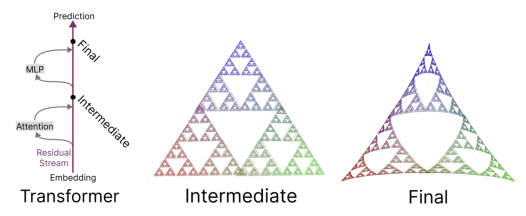
Evolution of the belief state geometry for Mess3, from constrained to optimal — An example of how the belief state geometry can be warped in early layers due to architectural constraints in a transformer. These geometries are belief state geometries for Mess3 data, as studied in (Piotrowski et al., 2025) (from which this figure was taken). Here, the final form is matches that expected from optimal prediction, while the intermediate form follows from their given ansatz for constrained updating. This picture is elucidating, but an analogous form cannot hold for the RRXOR data we study below.

This picture of successive evolution through the transformer – from geometry associated to approximate then optimal prediction – is elegant and elucidating; however, we know it cannot exactly hold in general settings. An obvious obstacle to generalization is that the specific generating process (Piotrowski et al., 2025) studied had the nice property that belief state geometries could be found localized to single layers within the residual stream. However, even for other simple processes studied in (Shai et al., 2024), it was found that the belief state geometry could only be found in a concatenation of the residual streams after every layer in the transformer.

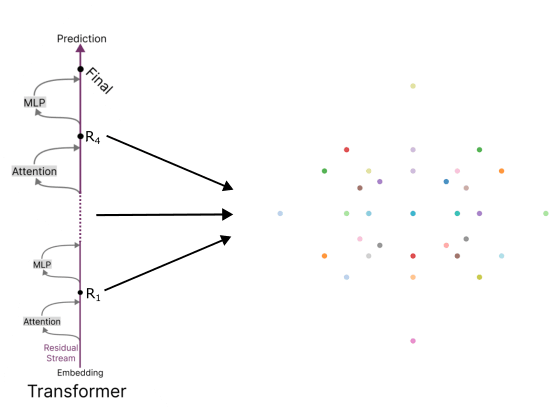
Depiction of the extraction of the belief state geometry for RRXOR, which requires concatenating activations from the residual stream after every layer — Unlike the Mess3 data depicted above, for the RRXOR process studied here, the belief state geometry can only be found after concatenating activations after every layer of the transformer. This means that the nice picture of evolution from geometries associated with constrained to exact prediction cannot hold for this process. It thus remains mysterious how the transformer overcomes the parallelized constraints of its architecture to build its world model.

In the work described below, we take some preliminary steps to understand how transformers can form optimal world models, despite architectural constraints, for one of these non-localized data generating processes, concentrating on the Random-Random-XOR (RRXOR) process. We find that the ansatz for constrained updating given in (Piotrowski et al., 2025) seemingly fails to generalize to this setting (instead predicting that the only non-zero updates to the residual stream come from tokens attending to themselves). Despite this, we empirically study the attention patterns of our transformer, finding preliminary evidence of some of the signatures of constrained updating found in (Piotrowski et al., 2025) carrying over.^[1] If these empirical results prove to be robust, they may suggest modifications to the ansatz of (Piotrowski et al., 2025). We expect that this more general ansatz will help in identifying the exact circuitry by which transformers build and use world models for this data. Ultimately, we expect these same tensions between architecture and accurate world models to be present in natural language settings relevant to AI safety, such that resolving these tensions even in individual examples may shed light on the processes by which LLMs form and utilize models of the world.

Background

As in (Piotrowski et al., 2025; Shai et al., 2024), we focus on data generated by an edge-emitting Hidden Markov model. For these systems, next-token emissions are associated with transitions between underlying (hidden) states of the system. Here in particular, we study the Random-Random-XOR process, which consists of sequences of 0s and 1s. After two tokens are randomly emitted, the next token in the sequence is determined through an exclusive-or (XOR) of the previous two tokens. This pattern is then repeated, with every third token being deterministic. As depicted in the figure below, there are 5 possible hidden states associated with this process; each arrow denotes a transition between states, and the arrow labels “a: p%” denote that the transition has a p% chance of occurring from the initial state, and is associated with emission of token a. For example, starting from the hidden state S_s, there are two possibilities (both occurring with equal probability): emission of a 0 token along with a transition to the state S₀, or emission of a 1 token along with a transition to the state S₁.

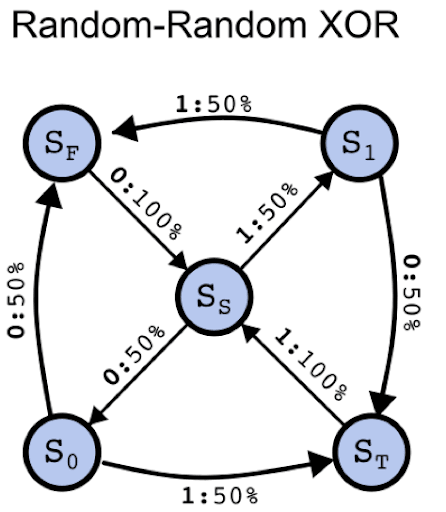
Depiction of the emission and state transition probabilities of the RRXOR process — The token emission and state transition probabilities associated with the RRXOR process. Figure taken from (Shai et al., 2024).

Optimal prediction of such data requires our language models to learn not only the structure behind the data generating process, but to further try to discern the hidden state that the process is currently in, given the context of previously seen tokens. For the RRXOR process, this means that given some sequence of tokens, e.g. 0110, we need to make a best guess as to which tokens are randomly generated and which are deterministically given by the previous two. Since there are multiple consistent possibilities for the sequence 0110, we can at best form a probability distribution over the possible hidden states we could be in at the last seen token. Each additional observed token allows us to update this probability distribution (or belief state). For the sequence 0110, if the next emitted token was 0, for example, we could conclude that this was a random token (since it is not the XOR of the previous two tokens 0 and 1), which sets the probability of then being in state S_s to zero.

Optimal beliefs about the probability of being in any particular hidden state can be represented as points in a probability simplex, the corners of which represent certainty of being in a particular state. For RRXOR, probability distributions over these states naturally live in a 4-simplex (which has 5 corners, corresponding to the 5 hidden states depicted above). The set of possible belief states for RRXOR is finite: there are only 36 distinct probability distributions that can arise from the recursive, optimal prediction as dictated by computational mechanics, updating along any RRXOR sequence. Though this simplex and the corresponding probability distributions naturally live in 4 dimensions, they can be visualized by projecting down to 2 dimensions, as seen in the figure below.

Belief state simplex for the RRXOR process — The belief state geometry for the RRXOR process, projected down into 2 dimensions. Each dot represents one of the 36 distinct optimal belief states associated with the process (with some states overlapping in the projection).

As additional tokens are generated and observed, optimal predictions for belief states evolve through updating, forming trajectories between points in this simplex. Collections of trajectories explore this simplex, building out nontrivial geometric patterns. These geometries are often highly complex and self-similar, though for RRXOR the geometry is particularly simple. The self-similarity of these geometric patterns formed by belief state probability updates are reflective of the recursive nature underlying the updates: finding the optimal belief state probability distribution after emitting the first i tokens requires knowing the optimal belief state probability distribution associated with emitting the first i-1 tokens, and so on.

These geometric patterns can be found in a transformer’s residual stream, suggesting that transformers are implementing this form of recursive updating associated with optimal prediction. How this world model is formed, how it is influenced by the underlying architecture of the transformer, and how exactly it is used by the transformer to make predictions, however, still need to be fully understood. In particular (and as mentioned above) the recursive updating associated with optimal prediction is naively at odds with the parallel computation enforced by the transformer architecture, in which the entire context-widow's tokens are processed through a given attention layer simultaneously.

In (Piotrowski et al., 2025), the authors suggested an ansatz for probability updating, giving an approximate update equation compatible with parallel token processing. From this ansatz, the authors were able to derive specific predictions for the form of the attention patterns and value-vector updates for their considered data process. In particular, they derived that the attention patterns exponentially decay with distance between source and destination tokens, and that the directions of value-vectors depend only on the source token. They then showed that these patterns (and an associated approximate belief state geometry) were present in the residual stream after the first layer, with later layers transforming this approximate geometry into the exact belief state geometry associated with optimal prediction (as depicted in the figure in the introduction).

However, while (Shai et al., 2024) studied several different hidden Markov models (finding belief state geometries in the residual streams for Mess3, RRXOR, and Z1R processes), (Piotrowski et al., 2025) simplified their analysis by focusing on data generated by just one process (Mess3). As noted in (Shai et al., 2024), for that process distinct belief states always have distinct next-token probabilities. (Shai et al., 2024) suggest that, as a result, transformers trained on this data must represent the belief state geometry in the final layer of the residual stream before unembedding. The RRXOR process is chosen here because it has no such simplifying property: some of the 36 belief states depicted above can have the same next-token probabilities, and so (Shai et al., 2024) suggest that because of this, the belief state geometry does not need to be maintained until the final layer of the transformer. Furthermore, for RRXOR, the belief state geometry could only be found in a concatenation of the residual stream across all layers.^[2] As a result, there is no clean separation between the formation of the constrained and exact belief state geometries, and as a result, no obvious way to understand how a transformer trained on RRXOR overcomes its architectural constraints to build its world model.

Experimental Implementation

To better understand how transformers builds its world model, we trained a 4-layer transformer with 4 attention heads per layer (with no layer normalization) on data generated by the RRXOR process described above. Additional details about this experimental setup can be found in a more detailed report and in the associated code for training and attention layer analysis. After training, our transformer achieves 89% of optimal accuracy (as measured by the ratio of theoretical minimal cross entropy to the cross entropy achieved at the end of training). We further verify the success of the training by the extraction of the belief state geometry, shown below (after feeding the transformer all possible context-window-sized sequences generated from the RRXOR process, concatenating the resulting residual stream activations across layers, and regressing onto the theoretically predicted geometry shown above to find the relevant subspace of the residual stream).

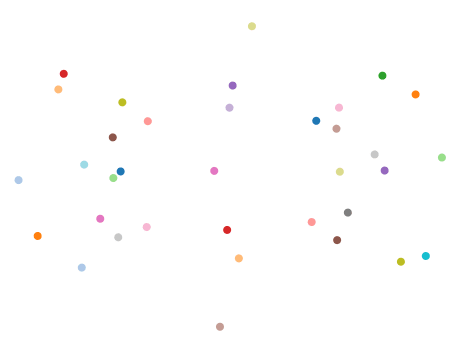
RRXOR belief state geometry, as extracted from our trained transformer — The belief state geometry for the RRXOR process, as extracted from the residual stream of our trained transformer and projected down to 2 dimensions. Each dot represents the average of all activations associated with each ground-truth belief state (for clarity of plotting). Small differences in color compared to the previous plot are unimportant (and due to points overlapping after projection).

Results

Theoretical Findings

As noted above, the expected attention patterns and value-vector properties found in (Piotrowski et al., 2025) for constrained updating were derived with Mess3 data in mind. Since the initial ansatz they used was general, however, we can plug in the various parameters relevant to RRXOR. When we do this, we find that this ansatz predicts

where $f$ is a linear map from the residual stream to the subspace containing our belief state geometry, $A_{d, s}$ are attention patterns for source token $s$ and destination token $d$ , and ${\to v}_{s}$ is the value vector for source token $s$ . This means that under this ansatz, updates to the residual stream are zero (except for $s = d$ ). This prediction is seemingly both in tension with the high accuracy that transformers are able to obtain and with the empirical results discussed next. This suggests that an update to the ansatz of (Piotrowski et al., 2025) is necessary.

Empirical Findings

Despite the lack of a theoretical lamplight to guide us, we nevertheless empirically analyze the attention heads for our transformer. Specifically, we look to match the empirical results of (Piotrowski et al., 2025), even if their mathematical ansatz no longer predicts these results. Interestingly, we also find decaying attention patterns, as depicted below. Unlike in their case, however, which found decaying attention in the first layer of their transformer, we find ours in the last layer. Additionally, the RRXOR parameter controlling the decay length is unclear (and may not even be consistent across heads).

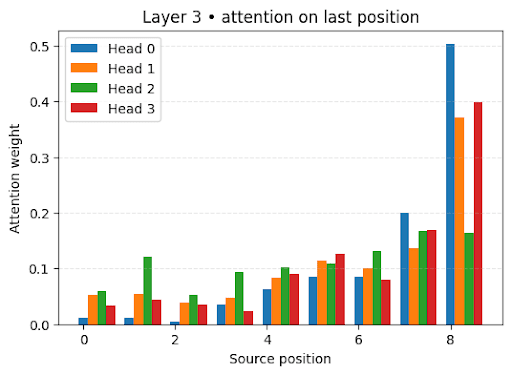
Attention patterns on the last layer of our transformer, with most consistent with exponential decay (though of differing decay lengths) — Attention patterns for the attention heads in the last layer of our transformer. Most heads show attention patterns consistent with the exponential decay found in (Piotrowski et al., 2025).

We also inspect the OV circuit. Here again, we find preliminary evidence of the structure of (Piotrowski et al., 2025) carrying over. We find value-vectors visibly clustering based on the two possible emitted tokens, as seen below (though this structure is far from the sharply parallel vectors found in (Piotrowski et al., 2025)).

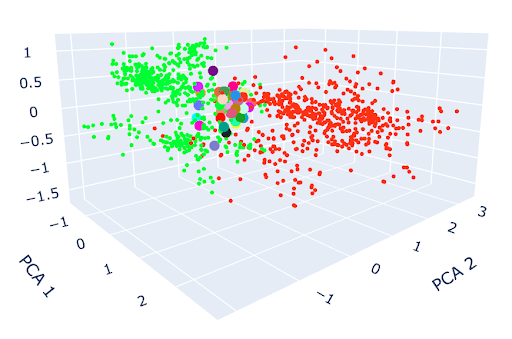
Value vectors, projected down into the subspace containing the belief state geometry. Vectors cluster based on the source token — The small dots represent value-vectors, projected onto the subspace of the residual stream containing the belief state geometry (this time depicted in three-dimensions, for clarity). Large dots indicate the belief state simplex. Vectors are colored by the source token, with 0 colored red and 1 colored green.

While we find the presence of both of these similarities with the structures found for transformers trained on Mess3 data, further analysis is necessary to determine how robust these patterns are and whether they are truly to be expected based on the underlying structure of RRXOR data. Nevertheless, we hope these observations are useful for forming a more general ansatz for constrained updating.

Limitations & Next Steps

Improving Empirical Results: Limitations for these results arise from the limited theoretical guideposts (arising from fundamental differences between the RRXOR process studied here and the previously studied Mess3 process) and still fuzzy empirical data (from limited experimentation with architectures and short training times).^[3] The next obvious steps are sharpening empirical results to determine whether they are robust (or just appeared here by happenstance) through additional experiments. Further, these additional experiments will also help to characterize whether the roughness in the clustering in OV value-vectors is due to an insufficiently trained model or is instead fundamentally limited. Likewise, additional experiments could shed light on whether the exponentially decaying attention patterns are always present (and if so, always in the last layer), and if the decay length is ubiquitous across experiments and architectures.
Finding a General Ansatz for Constrained Updating: We expect clearer empirical signals to help in forming a more general ansatz for constrained inference than that found in (Piotrowski et al., 2025). Further, while it was suggested in (Shai et al., 2024) that degeneracies in next token prediction were associated with the non-localized representation of the belief state geometry in the residual stream, this connection remains a bit unintuitive, but we suspect it is related to failure of the previous ansatz. Ultimately, we expect that better understanding of these properties can help elucidate the specific circuitry the transformer uses to build a world model, utilize it to perform predictions, and how intermediate computations done by attention layers fold into this process.
Building towards LLMs: Even with the generalization to data-generating processes which are only well represented by multi-layer transformers, this still represents a relatively narrow range of processes, vocabulary sizes, and architectures compared to the natural language LLMs of interest to AI safety. Additional stepping stones in this direction could involve yet more general data including the introduction of non-stationary processes (e.g, whose transition and emission probabilities change with time), non-ergodic processes (where the belief simplex consists of disconnected pieces), or where the number of hidden states is very large or infinite. Further, the formation of the belief state geometry was seemingly related to the model trying to implement optimal prediction. In natural language settings, exactly optimal prediction is mostly impossible, as underlying computations become unwieldy. Whether models continue to attempt to implement optimal prediction through the formation of a belief state geometries, or default to different algorithms completely, remains to be better understood.

Acknowledgements

We would like to thank Apart Research, PIBBSS and Timaeus for hosting the hackathon during which most of this work was completed.

^{^}
Note that this conclusion differs from that put forth in the original hackathon results. This comes from two sources: fixing small errors in the initial theoretical analysis for the attention pattern and fixing small errors in the empirical results for the value-vectors analysis.
^{^}
We do not know of an intuitive explanation for this observation, but may be related the ansatz of (Piotrowski et al., 2025), which implicitly assumes a single parallel computation, being incompatible with RRXOR.
^{^}
In particular, we used the same transformer as studied in the original hackathon report, (using the intervening time to fix errors/incomplete results in the theoretical analysis and value-vector analysis, rather than iterating on experiments).

LESSWRONG
LW