12
Infadistributions are exactly the natural hybrid of the two. I also associate (2) with formal logic.
The concept of infradistribution was defined here (Definition 7) although for the current purpose it's sufficient to use crisp infradistributions (Definition 9 here, it's just a compact convex set of probability distributions). Sharp infradistributions (Definition 10 here) are the special case of "pure (2)". I also talked about the connection to formal logic here.
Thanks! Quick question: how do you think these notions compare to factors in an undirected graphical model? (This is the closest thing I know of to how I imagine "notions" being formalized).
Hmm. I didn't encounter this terminology before, but, given a graph and a factor you can consider the convex hull of all probability distributions compatible with this graph and factor (i.e. all probability distributions obtained by assigning other factors to the other cliques in the graph). This is a crisp infradistribution. So, in this sense you can say factors are a special case of infradistributions (although I don't know how much information this transformation loses).
It's more natural to consider, instead of a factor, either the marginal probability distribution of a set of variables or the conditional probability distribution of a set of variables on a different set of variables. Specifying one of those is a linear condition on the full distribution so it gives you a crisp infradistribution without having to take convex hull, and no information is lost.
In everyday life, "notion" implies low-confidence. Often derogatory - low-confidence for the speaker, and a further implication that the holder/object of discussion doesn't even have the idea of confidence.
You might just use "proposition" or "claim" to mean the specific thing that a probability belief applies to.
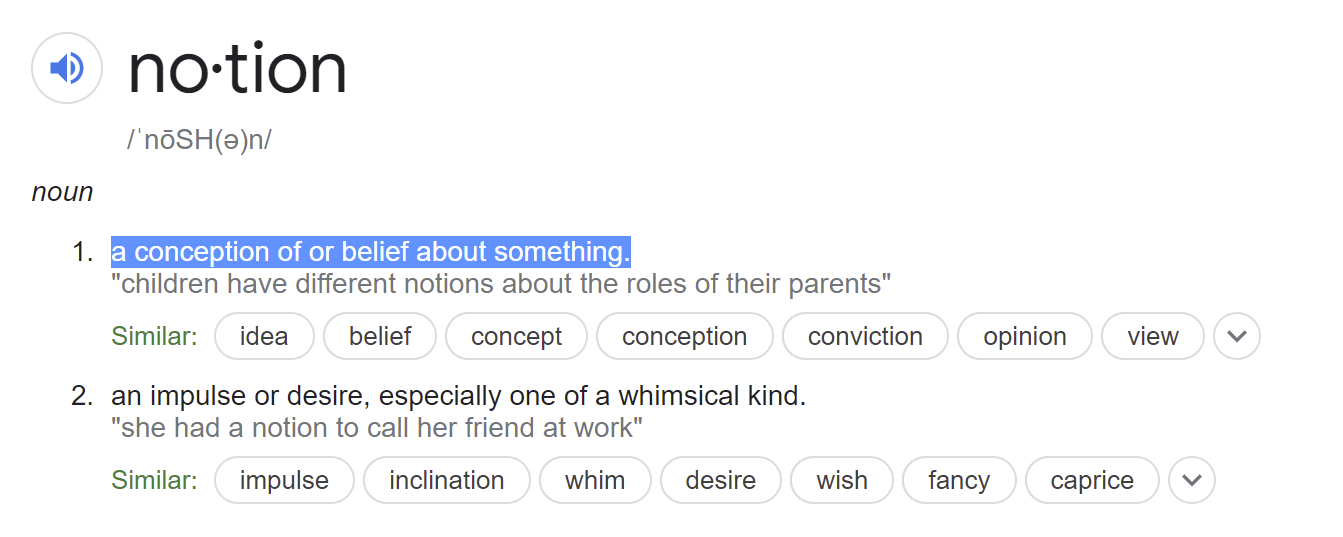
The term "belief" is used very differently in Bayesian ML and everyday life.
1) In Bayesian ML, is refers to a distribution over entire world models.
2) In everyday life, it refers to something more like a single proposition.
I propose the term "notion" for technical use to describe something like (2).