Here’s a typical abstract for a study of a drug that everyone knows works:
We study the efficacy of the drug Azadravapine on pain in a population of chronic pain sufferers. Azadravapine works by downregulating the CHNDA-2 pathway in the calcium channel gateways in the human brain. The target population was a patients in the United States who had been classified as suffering from chronic pain for at least three months. Patients were assessed on the clinical standard 100 point Blob-Allen pain scale before and after intervention. Compared to the placebo group, patients treated with Azadravapine saw a reduction in pain by an average of 6 points on the scale, representing a 0.4 ± 0.3 standard deviation decrease in pain level, with no evidence of treatment effect heterogeneity. The results reach statistical significance at conventional levels but the clinical significance of the effect size is uncertain.
This is surprising because Azadravapine is a drug that everyone knows works. Clinicians know it when they prescribe it and see immediate, miraculous reductions in pain. Patients know it when it allows them to function after years of trying to get through a day without considering suicide. And yet the gold standard RCTs are saying it has a treatment effect of just 0.4 standard deviations, the difference between a moderate annoyance and a slightly less moderate annoyance.
Furthermore, it doesn’t look like the drugs work strongly for some people and not others, which would be easier to believe. If that were true, we would expect to see the variance of pain in the treatment group to be greater than in the placebo group, but the variance looks about equal. I want to highlight this because it’s the most commonly given explanation for a low average treatment effect-that the drug works really well for some people but not others, which is all averaged together. Studies generally don't find evidence of this, however (this is an example for antidepressants).[1]
I made up the drug Azadravapine, but as Scott Alexander has noted, this is a common occurrence for real drugs, including those whose effects are nearly impossible to doubt like benzodiazepines. What might be happening here? Could clinicians and patients really be totally deluded by the placebo effect, attributing miraculous changes to the drug when really all you need is a placebo?
Maybe that’s true in some cases, and maybe even all cases, but I’d like to make an alternative case. It requires thinking about the placebo effect and the treatment effect a little differently, but it could explain why effect sizes always seem smaller and more homogeneous than it seems like they should be.
Setup
Consider a drug that is designed to treat a chronic condition, e.g. depression. Many people experience an episode of what could be considered depression at some point in their life but are not generally depressed. Others suffer from chronic depression and are hardly ever not feeling depressed. Others are in between.
When you run a clinical study on a drug to treat depression, you are inevitably going to capture a mix of group A and group B (and the in-betweens). For simplicity, let’s divide the clinical participants into just groups A (chronic sufferers) and B (transitory sufferers). Group B is likely to experience the placebo “effect” strongly. This is because the placebo effect is just the difference in symptoms between the after and before periods of the study, and group B was likely to get better on their own anyway. Since B are going to be mostly fine anyway, there’s not much extra the drug can do for them, so the extra treatment effect of the drug is likely not going to much for this group.
Group A, on the other hand, is not likely to see a large placebo effect, unless the condition is truly very susceptible to beliefs about treatment becoming a self-fulfilling prophecy. If instead we view the placebo effect as being mostly composed of ordinary mean reversion, the placebo effect for group A will be small. Here is a simplified table of what this might look like.
Let’s imagine what we would expect to see under this kind of setup. Remember, we’re thinking of a published paper that showed a small effect size-let’s say 0.5 standard deviations-and the variance of the placebo group post treatment is the same as the variance of the placebo group.
Example
This isn’t the only possible circumstance that would produce these results of course, but it is one such circumstance, summarized by the following table, with a . for parameters that don’t matter or don’t apply[2]
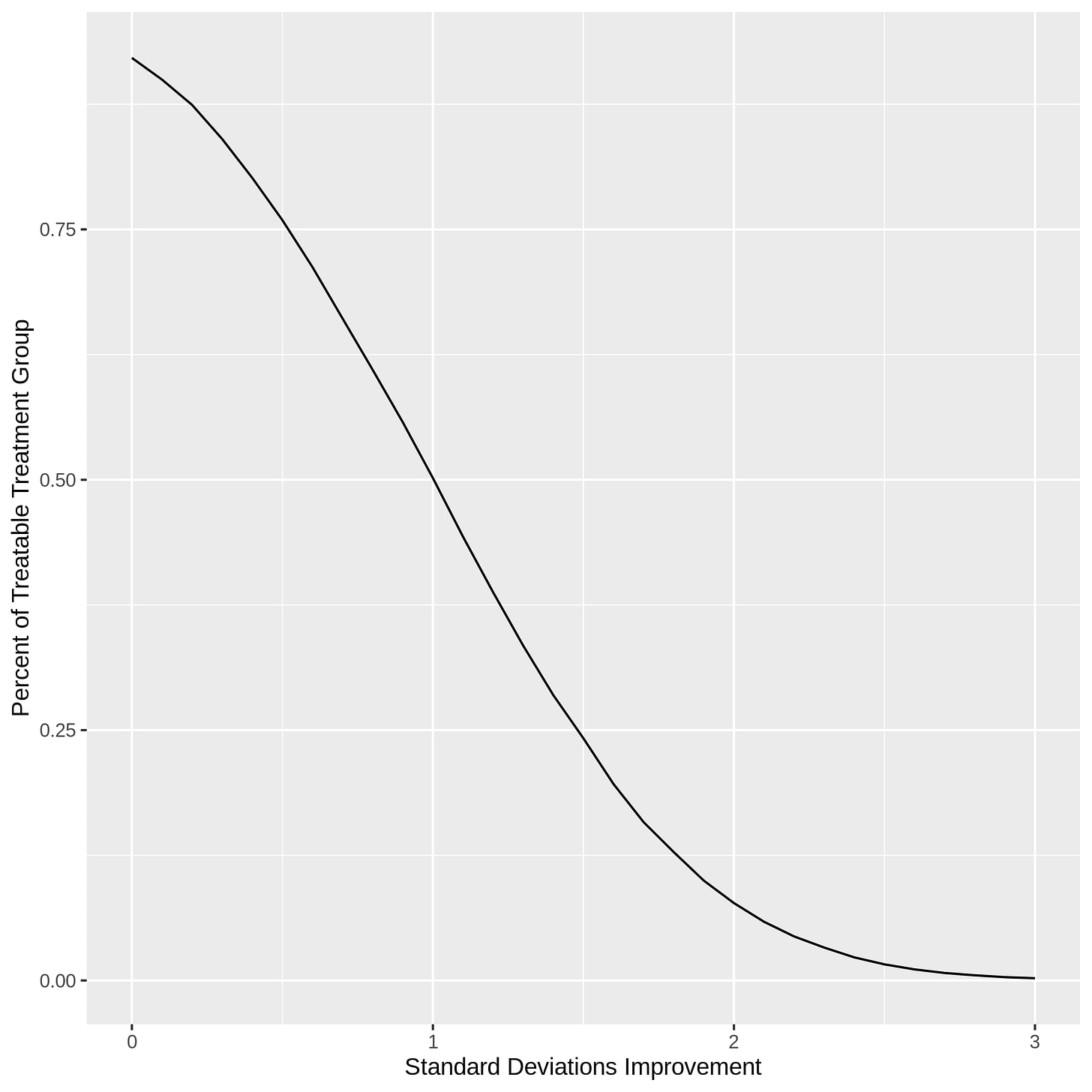
Under this model, the true average treatment effect (ATE) for group A, the only group that is actually susceptible to treatment, is 1 standard deviation, whereas the published ATE is 0.5 standard deviations. Already this is a huge difference, but it goes further, because there is actually substantial treatment effect heterogeneity even within the treatment group. This is possible even with the variance of the post-treatment group being equal to the variance of the post-placebo group because in the absence of a heterogeneous treatment effect, the variance of the post-treatment group would actually be smaller than the variance of the post-placebo group.
Treatment effect heterogeneity means that a substantial proportion of the treated population sees a treatment effect substantially bigger than 1 standard deviation from the treatment, with between 15% of the treatable population seeing a benefit of more than 2 standard deviations from the treatment. These are the patients that see a miraculous benefit from the treatment that seemed to be impossible given the headline results from the study.
Conclusion
The setup I described in this essay was chosen in large part for mathematical tractability. More realistically, susceptibility to the treatment or to the placebo would not be entirely mutually exclusive, and there’s certainly no reason to expect the sample to be split 50-50 between placebo responders and treatment responders. There’s also no reason to expect that the placebo effect for the placebo responders would be numerically the same as the treatment effect for the treatment responders.
Nevertheless, I think this example demonstrates that interpreting the effect size on clinical studies requires taking seriously the possibility that the population that is likely to show a large effect from the placebo is not the same as the population that will see an actual benefit from treatment. If this is the case-that is, there is a negative association between the placebo effect and the treatment effect-the actual treatment effect for those who actually require treatment can be both substantially larger and more heterogeneous than the headline results suggest. This has important implications for clinical study design and interpretation and may ease the mind of clinicians who see an irreconcilable gap between the effects they observe in their clinic versus in studies.
- ^
If you follow this link, you’ll see a glaring caveat: “Simulations showed that a large treatment effect heterogeneity is only compatible with the data if a strong correlation between placebo response and individual treatment effect is assumed.” That possibility is what I will explore in this essay.
- ^
The math for how to get these values is somewhat complicated, but the basic idea is intuitive. Denote a pre-treatment participant i as Xᵢ ~ N(μ, σ²), where μ is the mean pre-treatment value of our clinical outcome σ² is the variance. Consider the post-treatment participant i as Yᵢ ~ N(p, m²) and the post-placebo participant as Zᵢ ~ N(l, v²).
We then make several assumptions. First, half the placebo group sees a placebo effect and the placebo effect is homogeneous for these participants. Therefore, we divide the placebo group into two sequences: Y₁, Y₂, ..., Y_N/2 and Y_N/2+1, Y_N/2+2, ..., Y_N. We then add a constant (the placebo effect D) to the first group: Y₁ = X₁ + D₁, Y₂ = X₂ + D₂, ..., Y_(N/2) = X_(N/2) + D_(N/2). By the properties of variance, we get
- First half: Yᵢ ~ N(μ + D, σ²)
- Second half: Yᵢ ~ N(μ, σ²)
Since the two sequences have the same variance, the variance of the combined sequence is (1/2)(μ + D - (μ + D/2))² + (1/2)(μ - (μ + D/2))² = (1/2)(D/2)² + (1/2)(-D/2)² = D²/4.
Second, we are assuming that the expected value of the treatment effect (T) is equal to the placebo effect. That means that Teᵢ ~ N(D, h²) for some value of h.
Third, we are assuming that the variance of the post-treatment group as a whole is the same as the variance of the post-placebo group. We just showed that the variance of the post-placebo group is D²/4, where D is the placebo effect and the expected value of the treatment effect distribution. So we want to find some value h such that if Teᵢ ~ N(D, h²) for half the sample and Teᵢ = 0 for the other half of the sample, the resulting variance will be D²/4.
Since the post-treatment mean for both halves is the same since half get the treatment effect and half get the placebo effect, the variance of the combined sequence will be (1/2)σ² + (1/2)(σ² + D²) = σ² + D²/2. Setting σ² + D²/2 = D²/4, we get h² = (5C²/2 - 2σ²). This will be the variance of the heterogeneous treatment effect whose mean is D, the same as the placebo effect.
Now we have all the parameters identified to get the results that are typical of a clinical study: a calculated treatment effect of 0.5 standard deviations and a post-treatment variance equal to the post-placebo variance. In our setup, however, the actual effect size is much larger and more heterogeneous, even for the subset of participants who are susceptible to treatment.