Work done as part of my work with FAR AI, back in February 2023. It's a small result but I want to get it out of my drafts folder. It was the start of the research that led to interpreting the Sokoban planning RNN.

I was trying to study neural networks that plan, in order to have examples of mesa-optimizers.

I trained the recurrent maze CNN from Bansal et al. 2022 to solve 9x9 mazes, and applied it to a 33x33 maze. The architecture in their paper is a recurrent convolutional NN (R-CNN) that is regularized to be able to stop its computation at any iteration: during training, the NN runs for a random number of iterations before it is scored.

The task is supervised learning with inputs and labels like the following. The loss is cross-entropy.

Unrolling the R-CNN’s thinking

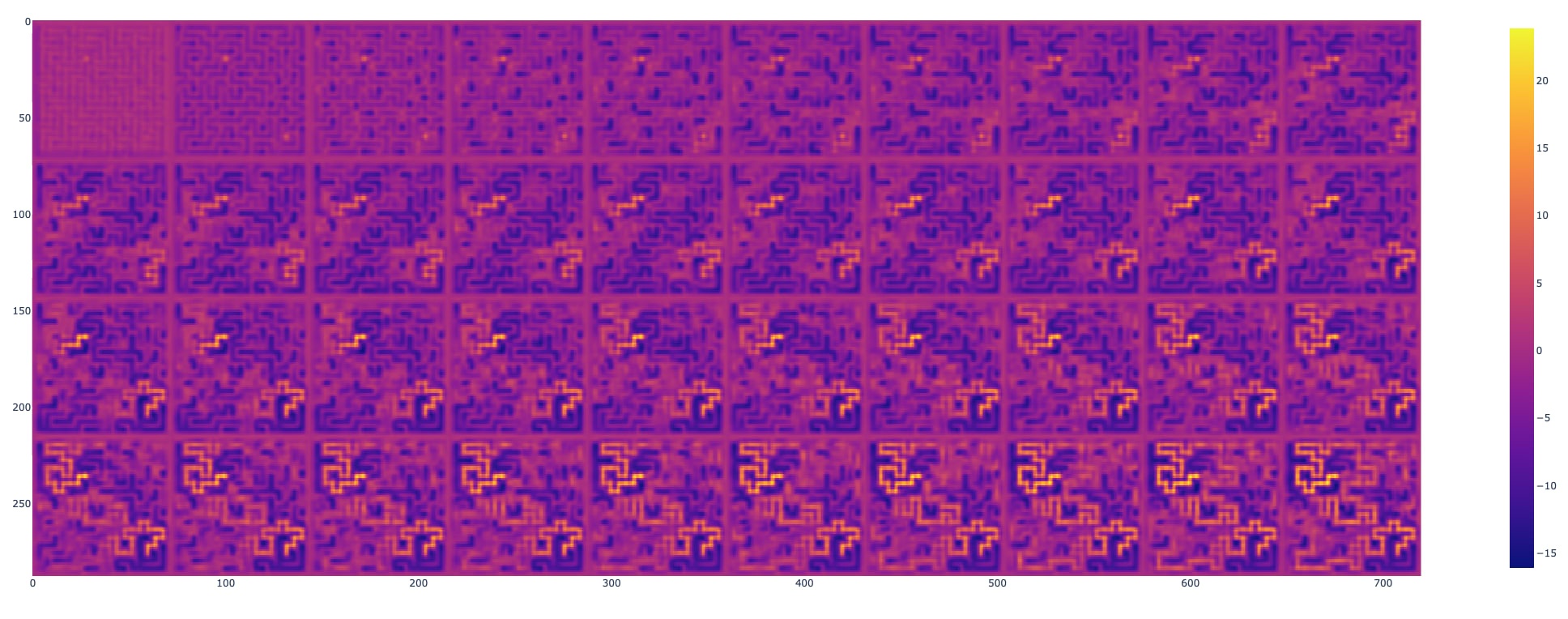
I set out to interpret the R-CNN. I plotted the output of the CNN as it evolves at each step. 

First of all note that simply connected mazes are a tree, so there is only one path between any two locations. Thus, the task is not to find the shortest path between source and goal, but any path at all! This is a very simple task.

Second, the RNN is encouraged to output workable solutions at any amount of iterations. Thus, it’s going to find an algorithm that takes as few iterations as possible.

Roughly the algorithm

This is based on the evidence in the picture above. Here’s the algorithm that I think this R-CNN implements:

• Detect clear dead ends; they can’t be between goal and source. These are white squares surrounded by black squares on 3 out of 4 sides.
  • (I think in this data generation they’re also characterized as white squares with 8 black squares out of 9 in their neighborhood)
• Paint the source/goal positive and the dead ends negative.
• At each iteration, spread the paints using something like flood fill
  • If you come to an intersection, wait until all but one of the paths have filled. (This is guaranteed to always happen because the maze is a tree, so recursively above the leaves at most one path is not a leaf, then at most one path is not a leaf-1, etc.)
    • If the paints were all negative, fill the intersection negative and continue
    • If there was a positive paint, fill the intersection positive and continue

Dead-end filling

After interpreting this NN I read the Wikipedia page on maze-solving algorithms, and found that the algorithm above is known as dead-end filling. See this video on it.

Implications for alignment

The algorithm is pretty clever, it’s simple and quick. It can optimize for connecting any two goals, and is thus technically a learned optimizer. However, the range of goals that it is able to optimize is very limited, and as such it is not very useful for studying more capable mesa-optimizers.