Note: This post summarizes my capstone project for the AI Alignment course by BlueDot Impact. You can learn more about their amazing courses here and consider applying!
Introduction
Recent research in weak-to-strong generalization (W2SG) has revealed a crucial insight: enhancing weak supervisors to train strong models relies more on the characteristics of the training data rather than on new algorithms. This article reviews the research conducted by Shin et al. (2024), who identified overlap density — a measurable data attribute that can predict and support successful W2SG. Their findings suggest we've been looking at the alignment problem through the wrong lens — instead of only focusing on model architectures, we should also be engineering datasets that maximize this critical density property. By analyzing their work and implementing their algorithms, I aim to provide researchers with tools to further investigate data-centric features that improve W2SG.
To apply the information from the article practically, you can use my research toolkit, which implements the overlap density algorithms mentioned in the research.
Background: W2SG's Data-Centric Foundation
Weak-to-Strong Context:
In the AI alignment paradigm first proposed by Burns et al. (2023), W2SG enables a weak model (e.g., GPT-2) to train a significantly stronger model (e.g., GPT-4) through carefully structured interactions. W2SG describes the transition from weak generalization, where a model performs well on “easy” patterns (i.e. patterns with clear, simple features or high-frequency occurrences in the training data), to strong generalization, where the model successfully handles “hard” patterns (low-frequency, high-complexity features). This becomes crucial when:
- Human oversight can't scale with AI capabilities
- We need to bootstrap supervision for superintelligent systems
- Developing failsafes against mesa-optimizers[1]
Current ML models often excel at weak generalization, but their capacity for strong generalization remains inconsistent and poorly understood. This gap has major implications for AI alignment: systems that generalize weakly may fail in unanticipated ways under novel conditions, leading to dangerous behaviors.
Key Definitions:
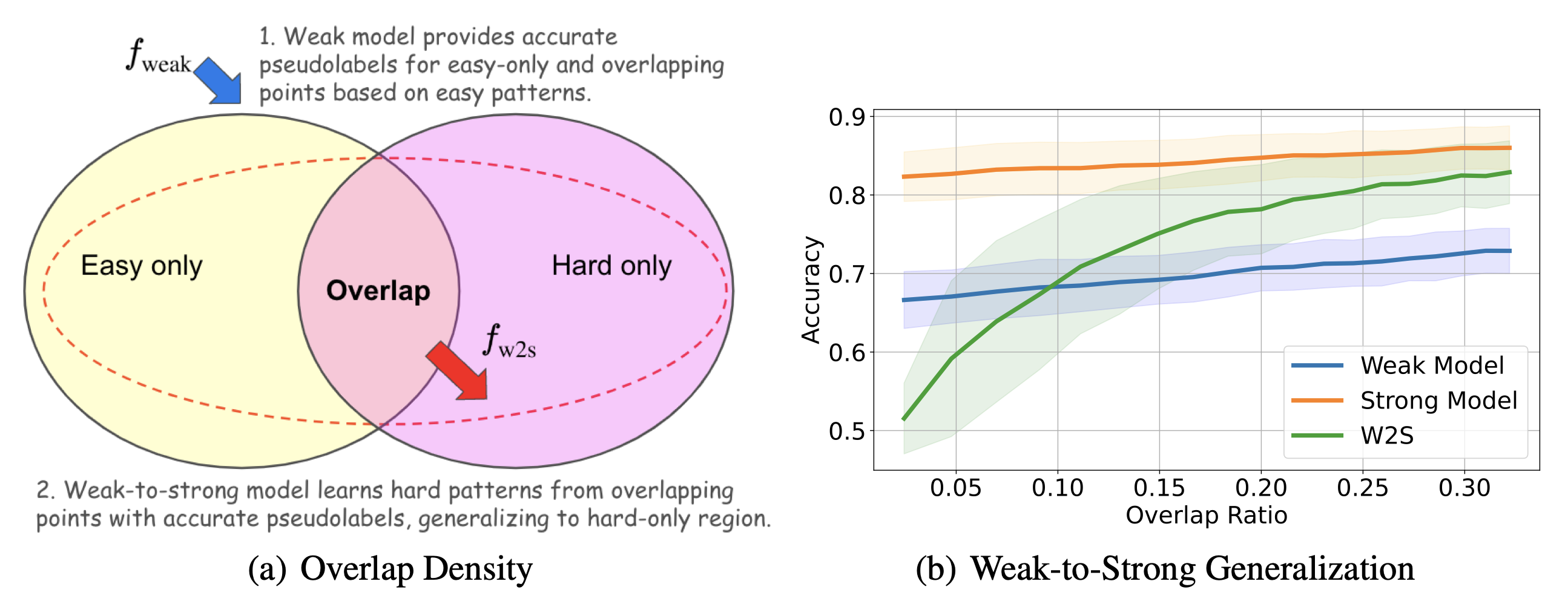
Figure 1: Concept behind Overlap Density and how it influences W2SG[2]
Shin et al. formalize easy patterns as features that are learnable by both weak and strong models. Conversely, hard patterns are only accessible by strong models as they require higher-order reasoning, and they tend to emerge as learning progresses.
A central challenge in W2SG is identifying conditions under which a model can bridge this gap from easy-to-hard patterns. Shin et al. hypothesize that overlapping structures between easy and hard patterns could facilitate this generalization.
Explaining Easy, Hard, and Overlapping patterns in LLM datasets via "How a Car Works"
In this particular example[3], a child (playing the role of a weak model — still learning the basics and struggling to reason about complex ideas) and an adult (plays the role of a strong model — capable of understanding complex ideas) learning about how a car works. The dataset consists of textual descriptions and examples related to cars. Easy, hard, and overlapping patterns represent different kinds of concepts within the dataset. In this scenario:
Easy concepts (basic, foundational knowledge):
- "If you push the gas pedal and then release it, the car will keep rolling because of momentum."
- "A car has four wheels, and the driver uses a steering wheel to turn the car."
- "Cars need fuel to run."
For the child (the weak model), these concepts are easy to understand and can be directly incorporated into their knowledge base. For the adult (strong model), these concepts offer little new information—they are already well-understood and don’t challenge the adult’s existing understanding.
Hard concepts (complex, interconnected knowledge):
- "A car’s engine uses pistons and cylinders to compress an air-fuel mixture and ignite it, producing energy through combustion. This energy pushes the pistons to rotate the crankshaft."
- "The transmission system adjusts the torque and speed ratio, allowing the engine's power to match the car’s speed requirements."
- "The alternator converts mechanical energy from the engine into electrical energy to recharge the car’s battery."
For the child, these concepts are overwhelming; they involve terms and processes (e.g., pistons, torque, transmission) that cannot be understood without additional foundational knowledge. For the adult, these concepts are more accessible, provided they already understand the easy concepts (e.g., how energy and motion interact). These hard concepts challenge the adult’s reasoning and allow the strong model to learn new, advanced relationships.
Overlapping concepts (bridging the gap between easy and hard):
- "The engine turns fuel into energy, which is transferred to the wheels via the drive shaft, a metal tube that moves power from the engine to the wheels."
- "The brakes on a car create friction to slow it down by converting the car’s kinetic energy into heat energy."
- "The power steering system reduces the effort needed to turn the steering wheel by using hydraulic or electric pressure."
Here’s where the generalization dynamic comes in:
- The child learns overlapping concepts from the prior knowledge of easy patterns. Through these concepts, the child can generalize parts of the dataset containing mixed (easy and hard) concepts. For example:
- The child might generalize: "The engine turns fuel into energy for the drive shaft."
- The adult learns from the child's generalization, refining its understanding of hard-only patterns. For example:
- The adult can now generalize from the information provided by the child to tackle previously unknown/incomplete concepts such as: "The drive shaft transfers rotational energy to the differential."
From a data-centric perspective, overlap density is a crucial property of datasets. It ensures that concepts are distributed in a way that facilitates W2SG:
- Weak models bootstrap the process by learning and labelling overlapping patterns, which improves generalization to harder concepts.
- Strong models leverage the weak model’s labelled data to reinforce and refine their deeper knowledge, ultimately improving their performance in a controlled manner
Overlap Density: The Data Multiplier Effect
Shin et al.'s central insight: W2SG succeeds when datasets contain sufficient "bilingual" examples where easy and hard patterns coexist (termed overlap density).
These overlap points act as Rosetta Stones that enable strong models to:
- Decode Hard Patterns - Use weak supervision as cryptographic keys to unlock latent complex features
- Extrapolate Beyond Supervision - Generalize to pure-hard examples through pattern completion mechanisms
- Filter Alignment-Critical Data - Identify samples where capability gains won't compromise safety guarantees[4]
The paper also identifies three distinct operational regimes through controlled experiments:
| Regime | Overlap Density | W2SG Outcome |
|---|---|---|
| Low | Insufficient overlap points or overly noisy detection | Worse than weak model (insufficient decryption keys) |
| Medium | Adequate overlap points and moderate noise levels | Matches/slightly exceeds weak model (partial pattern completion) |
| High | Sufficient overlap points with minimal noise | Approaches strong model ceiling (full cryptographic break-through) |
Here are a few experimental results:
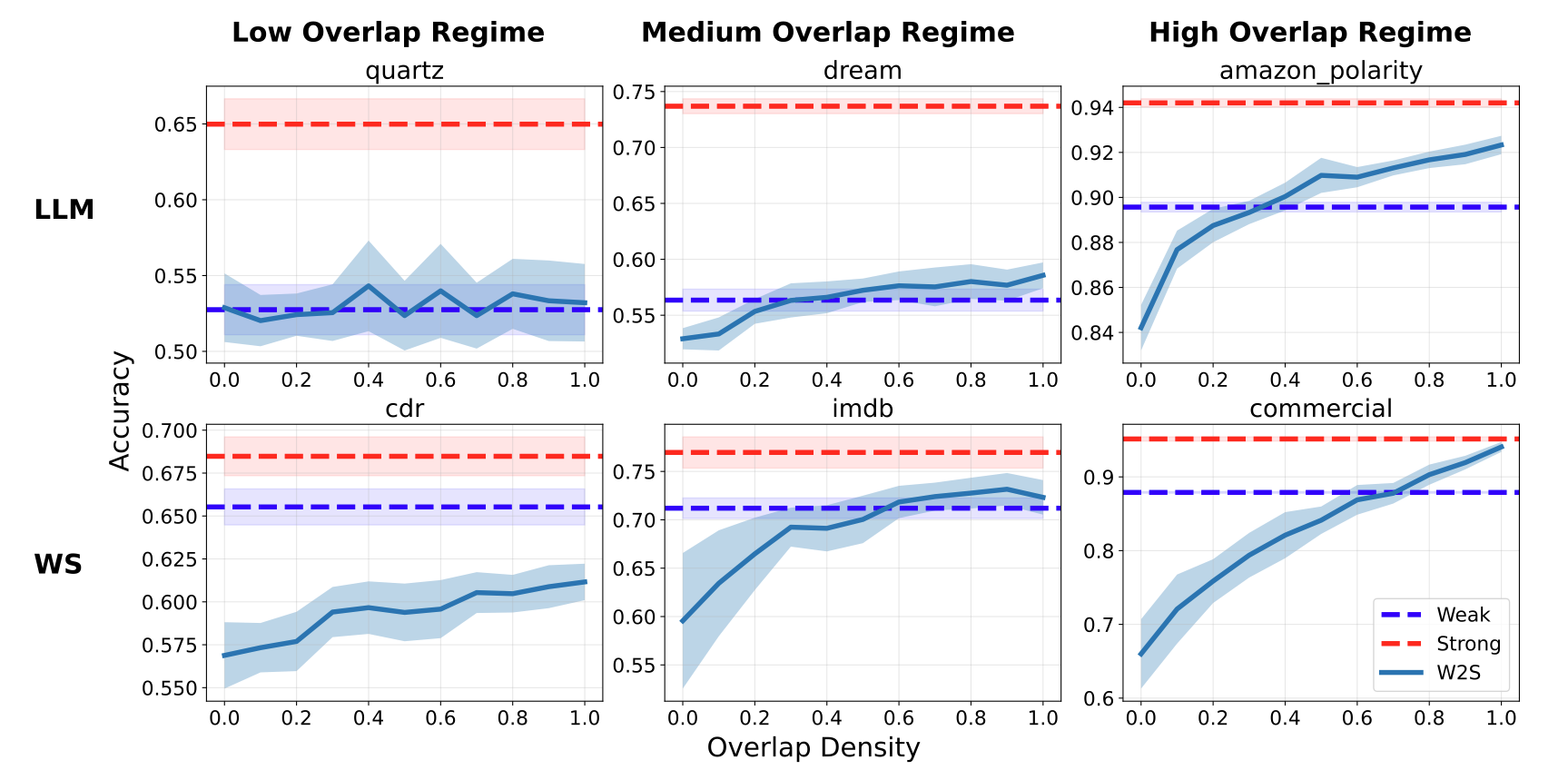
Figure 2: W2SG Performance vs overlap density regimes.[5]
The paper introduces two pivotal algorithms designed to identify and maximize overlap density in datasets:
Overlap Detection Algorithm
This algorithm identifies overlapping points in a dataset, which are critical for enabling W2SG.
- Purpose: Detect data points that contain both easy and hard patterns.
- How It Works:
- Separate Hard-Only Points:
- Confidence scores from the weak model are used to identify hard-only points (low-confidence predictions).
- The dataset is split into hard-only points and non-hard-only points.
- Detect Overlapping Points:
- For non-hard-only points, overlap scores are computed based on their similarity to hard-only points.
- Points with high overlap scores are classified as overlapping points.
- Thresholds for confidence and overlap scores are determined using change point detection techniques.
- Separate Hard-Only Points:
- Outcome: Isolates overlapping points effectively, allowing the strong model to learn harder patterns from these points.
UCB-Based Data Selection Algorithm
This algorithm is designed to prioritize data sources with the highest overlap density under a limited data acquisition budget. It uses an Upper Confidence Bound (UCB)approach to balance exploration and exploitation.
- Purpose: Identify which data sources are most likely to contain overlapping points (data with both easy and hard patterns) to enhance weak-to-strong generalization.
- How It Works:
- Each data source is sampled initially, and overlap density is estimated using the Overlap Detection Algorithm.
- The algorithm computes a UCB score for each source, combining the estimated overlap density with a confidence term to encourage exploration.
- The source with the highest UCB score is selected for further sampling.
- This process iterates, refining overlap density estimates and focusing on the most promising sources.
- Outcome: Efficiently allocates resources to maximize overlap density, improving the generalization capability of the strong model.
Analysis: Why This Changes Alignment Strategy
Key Findings
- Data AND Algorithms: Curating overlap points substantially improves W2SG without tweaking model architectures or training parameters[6]
- Overlap detection algorithm matters: Their UCB-based selection algorithm outperforms random sampling[7]
- Noise resilience: Overlap detection works even with 20% to 30%+ label noise through confidence thresholding[8]
This data-centric approach aligns with broader shifts in ML that emphasize the importance of data quality and properties over purely algorithmic improvements[9].
Broader Alignment Implications
This work suggests several paradigm shifts:
- Safety-Capability Balance:
High overlap density may resolve the alignment tax problem by making safety-preserving features necessary for capability gains.- Safety Datasets must be designed with overlap metrics.
The paper's theoretical framework (Section 3.1) shows that overlap density acts as an information bottleneck between weak and strong models. This means:- High overlap → Strong model inherits weak supervisor's safety properties
- Low overlap → Strong model diverges unpredictably
Capability Control emerges naturally from data constraints:
While Shin et al. don't explicitly test capability limitation, their core Theorem (4.1) proves that overlap density bounds strong model performance. A simplified interpretation (provided by Changho Shin) of Theorem 4.1:This suggests that W2S performance is bounded by a relationship between agreement rates on hard patterns and overlap regions. The W2S model's performance improves as agreement on overlap regions increases, creating a linear relationship between overlap density and performance gains.
The overlap density framework reveals a potential mechanism for creating intentional capability ceilings - a valuable tool for AI alignment. By controlling the distribution of overlap in training data, developers could:
- Establish boundaries around specific capabilities by limiting overlap in sensitive domains;
- Create "fenced" learning environments where certain generalizations are structurally inhibited;
- Implement staged capability development, where new capacities are only unlocked when appropriate overlap is introduced.
This represents a shift from post-hoc capability control to built-in limitations by design. However, for general-purpose systems, care must be taken to ensure these ceilings don't excessively restrict beneficial capabilities. Overlap engineering thus becomes a targeted approach to capability shaping rather than blanket limitation.
- Safety Datasets must be designed with overlap metrics.
Safety Through High-Overlap:
High-overlap datasets likely enforce safer generalization through several mechanisms. When overlap density is high, the strong model must learn hard patterns through their connection to easy patterns that the weak model can verify. This creates a natural "interpretability bridge" where any complex behavior must develop from simpler, understandable behaviors.Specifically, high-overlap training creates a constraint where the strong model's behavior on hard patterns must be consistent with its behavior on overlapping patterns, which in turn must align with weak model predictions. This forms a chain of verification that makes unpredictable generalizations less likely.
Additionally, because the strong model learns to recognize when hard and easy patterns co-occur, it may develop better calibration about when to apply certain kinds of reasoning, potentially reducing overgeneralization risks.
Overlap Density as a Safety Metric:
Low-overlap training runs could indeed serve as "red flags" for potentially dangerous capability jumps. When a model shows significant performance gains despite low overlap density, it suggests the model is learning hard patterns without verifiable connections to easy patterns - essentially developing capabilities the weak supervisor cannot comprehend or validate.This metric could be integrated into AI development pipelines, where:
- Overlap density is continuously monitored during training;
- Alerts trigger when performance improves faster than overlap density would predict;
- Training could automatically pause when such divergence occurs.
This approach provides a quantifiable, data-centric alternative to capability monitoring compared to more heuristic methods currently employed in AI safety.
Complementary Safety Approaches:
Overlap density offers a complementary approach to mechanistic interpretability efforts in AI safety[11]. While mechanistic interpretability focuses on reverse-engineering neural networks to understand their internal computations, overlap density provides a dataset-level perspective on what enables safe generalization.These approaches could work synergistically:
- Overlap detection algorithms could identify which training examples most influenced a model's generalization capabilities;
- Mechanistic interpretability could then target those specific examples to understand how the model represents and processes them;
- Together, they create a multi-level verification system where both the data and the model mechanisms are analyzed.
Unlike mechanistic interpretability, which faces significant scaling challenges with larger models, overlap density analysis remains computationally tractable even for very large models, as it primarily analyzes dataset properties rather than model internals.
- New Research Directions:
The exploration of overlap density paves the way for further innovative research possibilities, including:- Multi-Level Overlaps: Expanding the concept to N-way pattern intersections, enabling the analysis of more intricate patterns.
- Dynamic Density: Implementing adaptive sampling techniques during training that vary based on the current overlap regime and the resulting W2SG performance improvements.
- Adversarial Overlaps: Investigating the model's robustness against overlap poisoning to ensure stability and reliability in diverse scenarios.
Risks of Excessive Overlap
While much of this analysis focuses on insufficient overlap, excessive overlap density introduces its own risks. When almost all training examples contain both easy and hard patterns, the strong model may:
- Develop brittle correlations: learning to rely exclusively on easy patterns as gateways to hard ones;
- Fail to develop robust independent representations[12]: becoming unable to recognize hard patterns when they appear without corresponding easy patterns;
- Create an artificial coupling: where the model cannot process hard patterns without the "crutch" of easy ones.
These issues might only become apparent during deployment when the model encounters distribution shifts where the correlation between easy and hard patterns differs from the training data. This highlights the importance of balanced overlap engineering rather than simply maximizing overlap density.
A particularly concerning risk of excessive overlap is the potential for amplifying weak model biases. When a strong model is consistently trained on examples where hard patterns only appear alongside easy patterns that the weak model recognizes, it may:
- Inherit and potentially amplify biases present in the weak model;
- Develop blind spots to hard patterns that don't correlate with easy patterns in the training data;
- Learn to imitate superficial heuristics the weak model uses rather than developing deeper understanding.
The overlap detection algorithm could be extended to identify "diverse overlap" - ensuring that hard patterns connect to a variety of different easy patterns, reducing the risk of bias inheritance. This suggests an optimal overlap regime that balances quantity with diversity of overlapping patterns.
Implications for Scaling AI Systems
If overlap density is this crucial for weak-to-strong transitions, then why hasn't it been a major focus in mainstream ML research?
Despite its importance, overlap density has been largely overlooked in mainstream ML research for several reasons:
- Focus on architecture: The field has historically emphasized model architectures and training algorithms over dataset properties;
- Implicit optimization: Some training techniques may accidentally optimize for overlap density without explicitly targeting it;
- Measurement challenges: Without the overlap detection algorithms presented in the paper and the GitHub repo, quantifying this property was difficult.
This oversight has significant implications for current scaling practices. Many large-scale training runs likely rely on naturally occurring overlap rather than intentionally engineered datasets. This may explain why capability gains sometimes appear unpredictable or discontinuous - they might correspond to accidentally discovering regions of high overlap density.
As the field progresses, overlap density could become a standard dataset quality metric alongside more traditional measures. This would enable more predictable and controlled capability development, particularly for safety-critical systems where unexpected generalization could pose risks.
Research Toolkit: Implementing the Paper's Insights
To access the toolkit, please visit the GitHub repository.
The Overlap Density toolkit is a practical implementation of the concepts introduced in Shin et al.'s (2024) research. It focuses on analyzing and leveraging overlap density in training datasets. By providing tools to measure, analyze, and experiment with overlap density, the toolkit empowers researchers to explore how data-centric features can significantly enhance W2SG. This approach shifts the focus from purely algorithmic improvements to optimizing data properties for better performance.
The toolkit is designed for researchers aiming to:
- Investigate how overlap density facilitates W2SG between large language models (LLMs)
- Experiment with mixing overlapping and non-overlapping data points to study their effects on model performance
- Build upon Shin et al.'s findings to develop new alignment strategies that balance safety and capability
It includes implementation of both algorithms described in this article, along with example notebooks demonstrating their application to different datasets and models.
Key Features
- Dataset Processing: Prepares datasets for training, validation, and testing, ensuring compatibility with various formats.
- Model Initialization: Supports weak and strong models with optional configurations like Low-Rank Adaptation (LoRA).
- Overlap Density Calculation: Measures overlap density using activations and labels, with built-in threshold detection.
- Mixing Experiments: Enables controlled mixing of overlapping and non-overlapping data points to study their impact on performance.
- Visualization and Exporting: Provides tools for plotting results and saving metrics in JSON format for further analysis.
Potential Applications
- AI Alignment Research: Use overlap density as a metric to design datasets that promote safe generalization in AI systems
- Curriculum Learning: Develop training curricula where weak models bootstrap strong models by leveraging overlapping patterns
- Robustness Testing: Evaluate model resilience under varying levels of overlap density, including scenarios with noisy or adversarial overlaps
- Dataset Engineering: Optimize datasets for specific tasks by balancing easy, hard, and overlapping patterns
Conclusion & Call to Action
Shin et al.'s research on weak-to-strong generalization (W2SG) highlights the transformative role of overlap density in AI alignment. By focusing on dataset properties rather than solely on algorithms, they demonstrate how overlapping examples — where easy and hard patterns coexist — enable weak models to bootstrap strong ones, improving generalization while balancing safety and capability.
Key insights include:
- Overlap density bridges the gap between weak and strong generalization.
- Data-centric approaches can address alignment challenges like mesa-optimization[1] and scalable oversight.
This research opens new avenues for exploration. Researchers are encouraged to:
- Extend overlap density concepts to multi-level pattern intersections.
- Develop adaptive sampling strategies to optimize overlap density during training.
- Test robustness under adversarial or noisy overlaps.
- Collaborate across disciplines to refine these approaches and address broader alignment challenges.
By building on these findings, the AI community can advance toward safer, more capable systems while addressing critical alignment concerns.
Acknowledgments
I would like to express my profound gratitude to Changho Shin and colleagues for their groundbreaking work, which inspired me to do the analysis and toolkit. I also appreciate the EleutherAI team and their blog and the OpenAI team for their invaluable contributions and open-source code, which helped deepen my technical understanding of weak-to-strong generalization.
- ^
Mesa-optimization refers to when a trained ML system itself becomes an optimizer. This concept was introduced in "Risks from Learned Optimization" by Hubinger et al., where they explain that when neural networks develop their own internal optimization processes, they may pursue objectives different from those intended by the training process. This relates to Inner Alignment - ensuring that these emergent optimizers (mesa-optimizers) remain aligned with the base objective.
Overlap density may help prevent emergence of misaligned mesa-optimization by ensuring all learned patterns remain connected to verifiable weak-model patterns.
- ^
From the paper:
Left (a): overlapping easy and hard patterns in our dataset are the key to weak-to-strong generalization. Learning from overlapping points, where easy features and hard features coexist, enables a weak-to-strong model that can generalize, while is limited to reliably predicting points with easy patterns.
Right (b): adding more such overlapping points has little influence on the performance of the weak model, but dramatically improves the performance of the weak-to-strong model. Adding such points—even a small percentage of the dataset—can push against the limits of the strong model.
- ^
This example reflects my perspective on the concepts after analyzing the paper and working on the code for the past month. It can be flawed! Additionally, this serves as a fun and educational example inspired by my efforts to explain the inner workings of a car to my partner.
- ^
This is not an exhaustive list from my analysis.
- Pattern Isolation Guardrails where high-overlap data enables:
- Controlled Capability - limits learning to hard patterns verifiable through weak supervision
- Interpretable Updates - changes track measurable overlap metrics rather than black-box improvements
- UCB-Based Safety Filter. A pseudocode of possible implementation of Algorithm 1 (from the research paper) for this purpose:
def safety_filter(data_sources): for t in 1...T: # Estimate alignment risk inversely with overlap confidence safety_scores = [ 1/(1 + overlap_ci[source]) # Lower CI width = higher safety for source in data_sources ] selected = argmax(safety_scores) collect_data(selected)
- Pattern Isolation Guardrails where high-overlap data enables:
- ^
From the paper:
Red dashed (Strong) lines show strong model ceiling accuracies; blue dashed (Weak) lines represent weak model test accuracies; and W2S lines represent the accuracies of strong models trained on pseudolabeled data with a controlled proportion of overlap density.
The LLM label refers to their language model experiments, that are followed the setup described in EleutherAI (2024), which replicates Burns et al. (2023); and the WS label refers to weak supervision setting, where they used datasets from the WRENCH weak supervision benchmark (Zhang et al., 2021)
- ^
OpenAI mentions in their paper:
We are still far from recovering the full capabilities of strong models with naive finetuning alone, suggesting that techniques like RLHF may scale poorly to superhuman models without further work.
That's where overlap density comes in to improve W2SG performance from a data-centric perspective and as one of the powerful tools in the hands of researchers.
- ^
Some experimental results with their UCB-Based Data Selection for Maximizing Overlap vs random sampling:
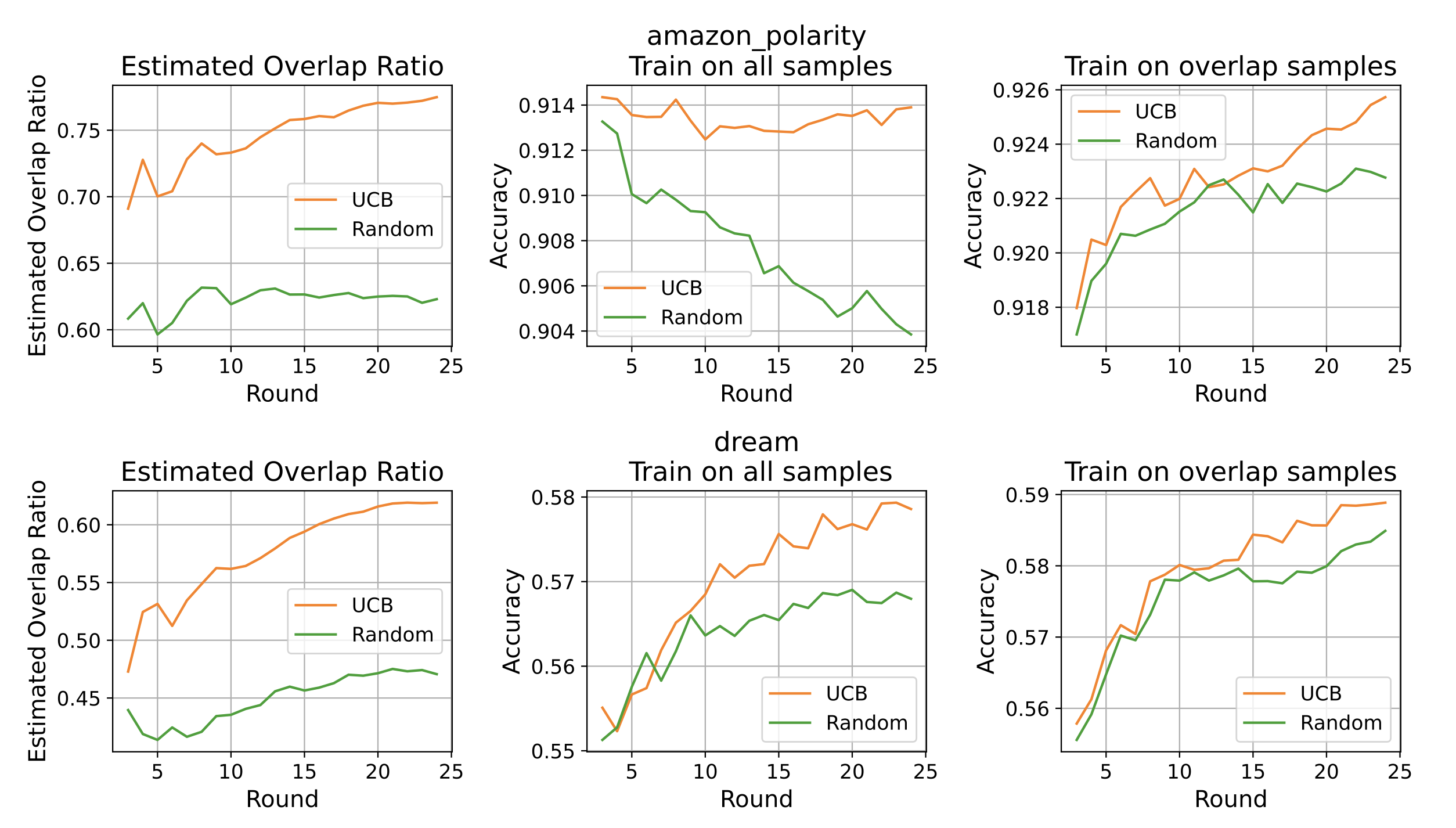
From the paper: "Data selection results with Algorithm 1 (UCB-based algorithm) for Amazon Polarity and DREAM datasets. We report the average of 20 repeated experiments with different seeds. We observe that the data source selection procedure, based on overlap density estimation, can produce enhancements over random sampling across data sources."
- ^
According to the synthetic experimental results, a weak-to-strong (W2S) model still outperforms a weak model with 30%+ of mixed noise (from the sampling process and overlap detection)
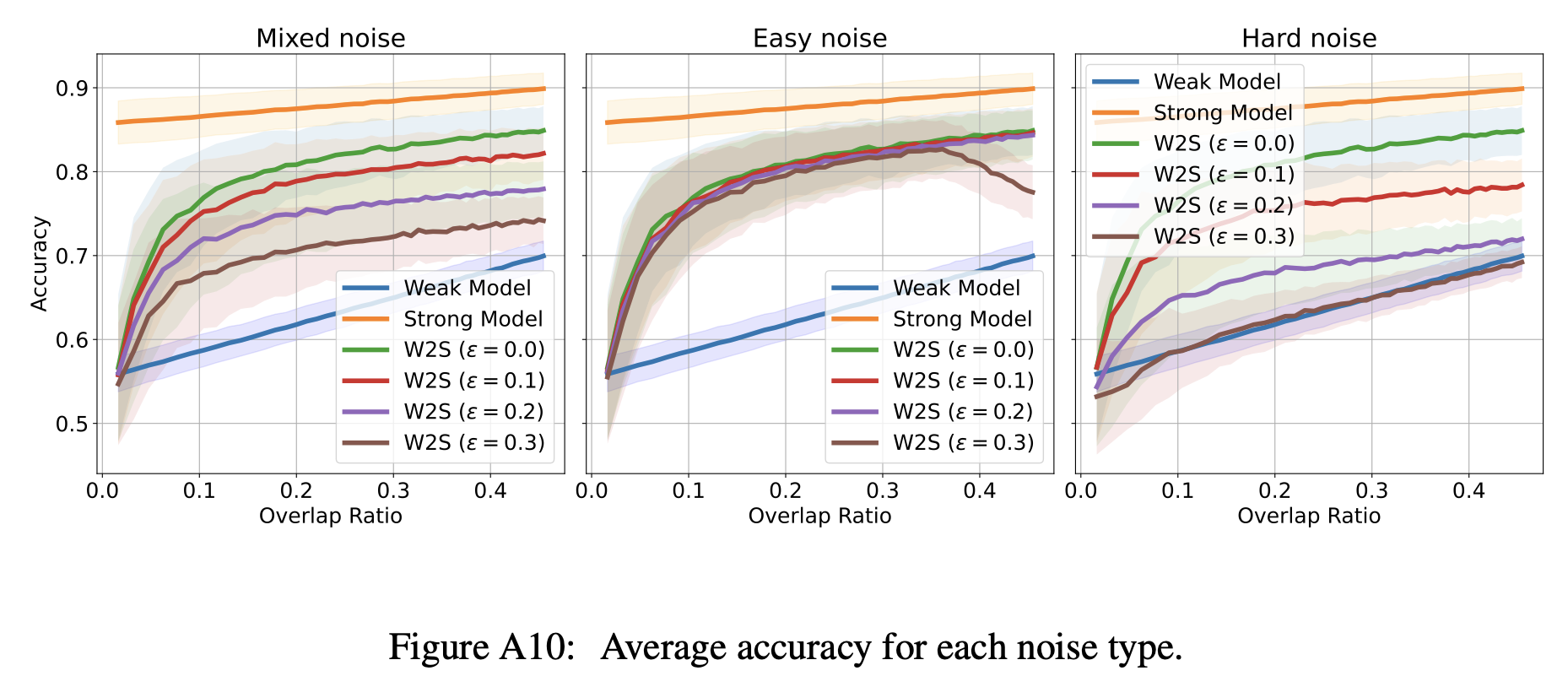
From the paper: "These scenarios are as follows:
(1) Mixed noise: Half of the errors select easy-only points, and the other half select hard-only points;
(2) Easy noise: All errors select easy-only points;
(3) Hard noise: All errors select hard-only points."In practice, noise may be introduced from a sampling process or overlap detection algorithm.
- ^
For more on data-centric approaches to AI, see Andrew Ng's work on Data-Centric AI
- ^
W2S performance on D_hard ≤ Agreement on D_hard + Weak model error rate on D_hard - Agreement on D_overlap
- ^
For a comprehensive review of mechanistic interpretability, see "Mechanistic Interpretability for AI Safety: A Review"
- ^
Recent research by Xue et al. (2025) provides complementary insights on how model representations shape weak-to-strong generalization, offering additional theoretical grounding for the overlap density framework: Representations Shape Weak-to-Strong Generalization: Theoretical Insights and Empirical Predictions