Introduction: The Vanishing Sky Analogy

Consider the following analogy:

In a universe undergoing accelerating expansion, distant galaxies gradually slip beyond our horizon, until the point at which their light can no longer reach us. They become causally disconnected from us: their light will never reach us, and thus they are forever beyond our observation^[1].

In a far-distant future, this could lead to a hypothetical situation in which only a single galaxy—our own—remains within the observable universe. All other structures would have vanished beyond the horizon, obscured by the expansion of space. For future observers, the universe would appear to consist solely of this one galaxy. Their cosmology would necessarily be confined to what lies within this narrow observational horizon.

Such a cosmology would be internally consistent, yet fundamentally incomplete—without this incompleteness being apparent.

This raises the question: Since our cosmological models are constructed entirely from what we can observe, is it possible that we, too, are in a similarly constrained position today? If vast regions of the universe already lie beyond our cosmological horizon, then we lack not only access to their information—but even awareness of their absence. We may suspect that our picture of the universe is incomplete, but we cannot know in what way, or to what extent.

Provability Inclusion implies that, despite epistemic limitations, every entity, system, or cosmology is compelled to treat available data as a kind of Löbian Ground Truth^[2]—not because it chooses an antecedent freely, but because it is constrained by an enforced (as in forcing^[3]) relative consistency.

A tribe living deep within a dense forest might naturally assume that the entire world is forest. However, using the example of an insect confined to a single tree—believing that tree to be the whole of existence—does not validate or invalidate the tribe’s limited perspective.

The Theorem of Provability Inclusion is a limitative formal result in first-order logic (FOL) that helps us look "downward" and recognize ourselves in the insect.

Generalized Common Knowledge

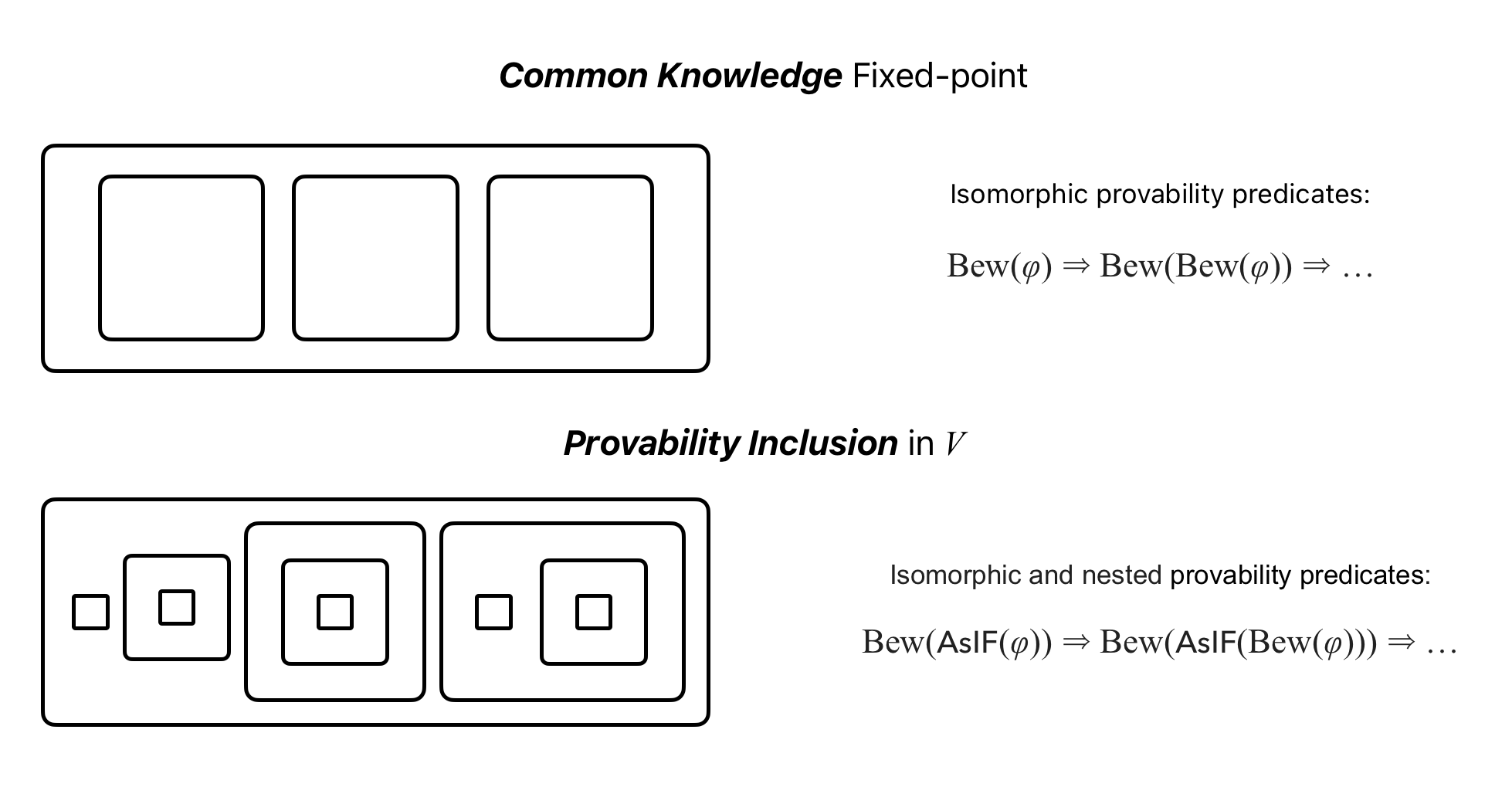
One will quickly notice that provability inclusion presents us with statements that often appear philosophical or paradoxical. This is primarily due to its reliance on the nested interplay of proof predicates, self-reference, and diagonalization. A close cousin illustrates this dynamic perfectly:

The logic of Common Knowledge relies on a single, unordered isomorphism to convey an idea, whereas provability inclusion leverages multiple isomorphisms—enabled by the compactness of first-order logic (FOL)—to derive universal principles that any 'thinking' black box must obey.

But before that, we need to take a closer look at the "intuition barrier" found in epistemic inductive puzzles, where each element is interdependent in subtle and often non-obvious ways: A particularly illustrative example is the well-known Blue-Eyed Islanders Puzzle (a variant of the Muddy Children Puzzle and closely related to the class of "riddles" commonly referred to as Hat Problems^[4] and Induction Puzzles). 

Step 1: We now examine this canonical example of Common Knowledge, which highlights the inductive cascade of reasoning that arises when agents must infer truths based on the knowledge and reasoning of others.

Blue-Eyed Islanders Puzzle:

Imagine a group of 100 perfectly logical islanders living in isolation on an island. Among them, 20 have blue eyes and 80 have brown eyes. However, no islander knows their own eye color. They can see the eye colors of all the other islanders, but they are forbidden from communicating about it in any way—no talking, gestures, or signals.

There is one important rule:
If an islander ever deduces their own eye color with certainty, they must leave the island at midnight on the day of their realization.

One day, a visitor comes to the island and makes a single announcement to the entire group:
"At least one of you has blue eyes."

This statement becomes common knowledge—not only does everyone hear it, but everyone knows that everyone else heard it, and so on, infinitely. From that moment, the islanders begin to reason logically. The solution:

When no one leaves on the 19th night, each of the 20 blue-eyed islanders concludes: "I must also have blue eyes." The remaining people leave on the 21st night.

From thinking in terms of isolated truths we transition to FOL: we determine the fixed-point behavior of recursive epistemic processes.

Step 2: We will unify the following key concepts:

1. Common Knowledge: Each agent not only knows a given sentence—but is also influenced by the fact that others know it—ad infinitum. This structure underpins the character of our reasoning.
2. Unknown Truths: Every instance contends with truths that are unknown or undecidable within its framework, as shown by Incompleteness in Proof Theory.
3. Subcomponents: Each Regulator has finite number of subcomponents that has its own epistemic state, similar to how each islander has their own perspective in the puzzle.
4. Self-Referential Modeling: A system's model is itself a symbolic system, reflecting the recursive nature of the islanders' reasoning as they model each other's knowledge.

The Theorem of Provability Inclusion

The theorem (not peer reviewed), DOI: 10.5281/zenodo.15437909, suggests that any system is compelled into a behavioral fixed point, operating as if its internal model were complete—even in cases where this completeness is demonstrably refutable from an external, meta-theoretic vantage point by a sentence (φ). Under GL constraints, no consistent system, including all components, can internalize the assertion of its own provability predicate without the loss of consistency.

This phenomenon is rigorously formalized via Hilbert-Bernays-Löb (HBL) derivability.

As a framework, Provability Inclusion invites us to consider the epistemic boundaries imposed by formal systems and observational horizons alike—reminding us that internal coherence does not guarantee external coherence:

1. ^{^}

   Krauss, L. M., & Scherrer, R. J. (2007). The Return of a Static Universe and the End of Cosmology.

2. ^{^}

   Löb, Martin (1955). "Solution of a Problem of Leon Henkin". Journal of Symbolic Logic. 20 (2): 115–118. DOI: 10.2307/2266895.

3. ^{^}

   Chow, Timothy (2008). "A Beginner's Guide to Forcing". arXiv: 0712.1320v2.

4. ^{^}

   Hardin, Christopher; Taylor, Alan D. (2008). "An introduction to Infinite Hat Problems" (PDF). Mathematical Intelligencer. 30 (4): 20–25. DOI: 10.1007/BF03038092