This post assumes knowledge of category theory, finite factored sets, and Bayes nets.

The Setup

I've already talked about DAGs and factor overlap Venn diagrams in a previous post, where I studied them within a category-theoretic framework. Here I'll also perform an explicit construction of them using set theory.

DAGs

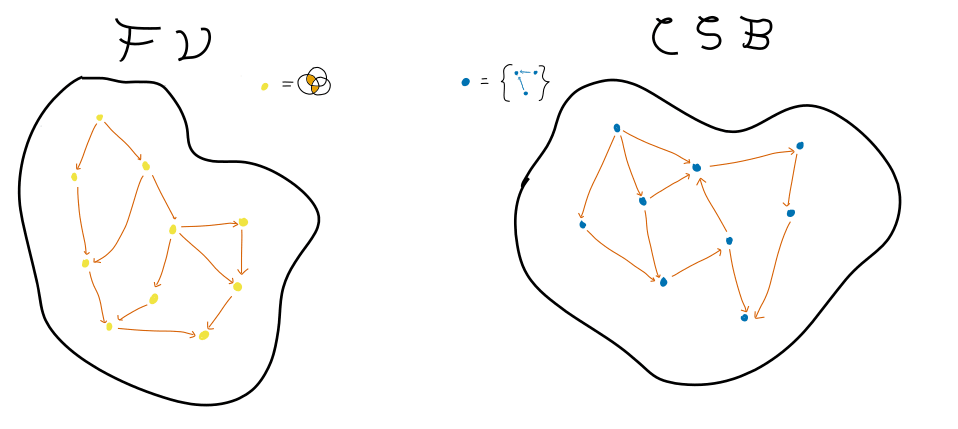
I have already discussed the set of directed acyclic graphs over $n$ elements. We will denote the set of all DAGs of $n$ elements as $DAG\left(n\right)$. Each Bayes net can be thought of as a set of pairs of elements $\left\{\right(i\in \{1,...,n\},j\ne i\in \{1,...,n\}),...\}$. 

This set can be converted into the category of Bayes nets over $n$ elements by the addition of morphisms corresponding to "bookkeeping"-type relationships, which we will denote${DAG}_n$. From this category, we can form a category whose elements are sets of the elements of ${DAG}_n$, subject to the following condition on a set $S$:

(I'll slightly go against standard notation by using calligraphic acronyms for my category names i.e. ${DAG}_n$. I don't feel like any of my categories are definitely natural or useful enough to earn a "proper" bold name like ${DAG}_n$)

$\forall s\in S,b\in DAG\left(n\right),s\to b⟹b\in S$

This means that, if we can reach a given Bayes net $b$ from any element $s$ of our set $S$, that Bayes net $b$ must also be in $S$. I refer to these as compatible sets and denote the category ${CSB}_n$ (standing for compatible sets of Bayes nets) as the category whose elements are compatible sets of $n$ elements and for any two elements. To write it out fully:

$Ob\left({CSB}_n\right)=\{S\in P(DAG\left(n\right))|\forall s\in S,d\in DAG(n),{DAG}_n(s,d)=\{\to \}⟹d\in S\}$

${CSB}_n(A,B)=\{\begin{array}{cc}\{\to \}& A\supseteq B\\ \left\{\right\}& A\subset B\end{array}$

This should be read as "There is a unique morphism from $A$ to $B$ if and only if $A$ is a weak superset of $B$, otherwise there is no morphism". Orderings of this form always follow the rules required to create a category.

(Aside: sometimes we think about equivalence classes of Bayes nets. If we choose, we can first convert our Bayes nets to equivalence classes, then convert them to compatible sets, but this is not needed here)

This category has an initial object ${Dis}_n$ which is a set consisting of the discrete Bayes net (with no arrows at all) and therefore all Bayes nets. Less trivially it has a terminal object ${Ind}_n$ which contains exactly the Bayes nets which have an arrow between every pair of objects.

Venn diagrams

Presence/absence Venn diagrams of $n$ elements can be thought of as elements of the power-set of the power-set of the set $\{1,...,n\}$. We can write this as $P\left(P\right(\{1,...,n\}\left)\right)$, but I will abbreviate this by writing $PP\left(n\right)$ in future. As before, we can form a category by ordering the sets, but in this case we will reverse the order of the morphisms, to create the category ${FV}_n$ (standing for factor Venn diagrams).

$Ob\left({FV}_n\right)=PP\left(n\right)$

${FV}_n(A,B)=\{\begin{array}{cc}\{\to \}& A\subseteq B\\ \left\{\right\}& A\supset B\end{array}$

This category has an initial object $\left\{\right\}$ and a terminal object $P\left(1,...,n\right)$. 

Our categories look (something) like this:

The Payoff

Functors $F_n$ and $G_n$

There exist functors ${FV}_n\stackrel{F_n}{\underset{G_n}{\rightleftarrows }}{CSB}_n$ which are naturally-defined with respect to the properties of joint probability distributions. There exist subcategories ${FV}_n^{\prime }$ and ${CSB}_n^{\prime }$ on which the functors $F_n$ and $G_n$ are totally inverse. The resulting category structure - I hope - will be useful for causal inference.

We will define compatibility $Cmp(a,b)$ between a set of elements $a\subseteq \{1,...,n\}$  and a Bayes net $b\in DAG\left(n\right)$ as follows: there must exist some node $a_i\in (a\hookrightarrow b)$ (the hook arrow $\hookrightarrow$ denotes the "inclusion" of the elements of $a$ into $b$, so it refers to the nodes in $b$which are elements of $a$) such that all other nodes $a_{\overline{i}}\in (a\hookrightarrow b)$ are reachable via paths including only elements of $a\hookrightarrow b$. 

$F_n:{FV}_n\to {CSB}_n$ maps an object  $V\in Ob\left({FV}_n\right)$ is mapped to an object $S\in Ob\left({CSB}_n\right)$according to the following rule: a Bayes net $s\in DAG\left(n\right)$ is present in $S$ if and only if  $Cmp(v,s)$ holds for every set $v\in V$.

We will quickly verify that this respects morphisms. Any $W$ such that $V\to W$ must contain at least all of the sets present in $V$ (since $V\to W⟺V\subseteq W$) and possibly more. Therefore, any $r\in R=F_n\left(W\right)$ must also follow all of the constraints imposed by $F_n\left(V\right)$ and possibly more, so $S\supseteq R⟺S\to R$.

Next, we wish to define $G_n$. This requires a little finesse but isn't too difficult. We shall say that $G_n:{CSB}_n\to {FV}_n$ maps an object $S\in Ob\left({CSB}_n\right)$ to an object $V\in Ob\left({FV}_n\right)$ according to the following rule: a set $v$ is present in $V$ if and only if $Cmp(v,s)$ holds for every Bayes net net $s\in S$.

You may notice that this is almost the reverse of $F_n$. This is by design. It's worth pausing for a moment to consider how they differ: $F_n$ maps a factor overlap Venn diagram, constructed as a set of sets of items from $\{1,...,n\}$, to a set of DAGs. We can think of it as starting with the complete set of DAGs, then going through our venn diagram $V$, and for each $v\in V$ throwing out the DAGs which don't conform. 

Conversely $G_n$ maps a set of DAGs to a set of factor overlaps. We can think of it as starting with the completely full factor overlap Venn diagram, and for each DAG $s\in S$, it throws out the factors which don't apply.

Quick Examples

Our functors are not quite inverses: for an example consider the Venn diagram corresponding to the set $\left\{\right\{\},\{1\},\{2\},\{1,2\},\{1,3\},\{2,3\left\}\right\}$ in ${FV}_3$. This is mapped by $F_3$ to exactly the set of totally connected DAGs, which is the terminal object in ${CSB}_3$. The terminal object in ${CSB}_3$ is mapped by $G_3$ to the terminal object $\left\{\right\{\},\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\left\}\right\}$ in ${FV}_3$. This corresponds to what I called "agnosticism" in our set of Venn diagrams in the last post.

Note that all objects $V\in Ob\left({FV}_n\right)$ such that $V=G_n(S\in Ob({CSB}_n\left)\right)$ will contain the elements $\left\{\right\}$ and $\left\{1\right\},...,\left\{n\right\}$. We will often write this as a $...,$ at the start of our set to save time.

For an example in the opposite direction, consider the set in ${CSB}_3$ which consists of the DAGs $\left\{\right(1,2),(3,2\left)\right\}$, $\left\{\right(2,3),(1,3\left)\right\}$ and the minimal set of other DAGs needed for this to be a valid element of ${CSB}_3$. This is mapped by $G_3$ to the set $\{...,\{2,3\left\}\right\}$, which is correspondingly mapped by $F_3$ to the set of DAGs "downstream" of $\left\{\right(2,3\left)\right\}$ and $\left\{\right(3,2\left)\right\}$. I left sets like this out of our category in the previous post.

As an example where our functors are inverse to one another, consider the initial object of ${FV}_3$, which is the empty set $\left\{\right\}$. This is mapped by $F_3$ to the initial object of ${CSB}_3$, which is the set containing all elements of $DAG\left(3\right)$. This is compatible with no shared factors (as any shared factors impose constraints on Bayes nets) so is mapped by $G_3$ right back to the empty set. This is true for any $n$. It also applies to the terminal objects of any ${FV}_n$ and ${CSB}_n$ i.e. the total power set $P\left(n\right)$ and the set containing only fully-connected Bayes nets.

Composing $F$ and $G$

I am going to be lazy here and omit the subscript $n$s, just imagine I've put them in while I'm talking about general properties of all $F_n$ and $G_n$. Consider the following sequence starting with an element $V\in Ob\left(FV\right)$:

$V\stackrel{F}{\to }S\stackrel{G}{\to }W\stackrel{F}{\to }R$

We have that $\forall v\in V,s\in S,Cmp(v,s)$. But $W$ is defined as the set of all elements $w$ (in the relevant set $P\left(\right\{1,...,n\left\}\right)$ for our given $n$) such that $\forall s\in S,Cmp(w,s)$. This means that all of our elements of $V$ are also elements of $W$, in other words $V\subseteq W$, and by the definition of our functor $F$, $V\subseteq W⟹S\supseteq R$.

But consider that we can reverse the logic: $\forall s\in S,w\in W,Cmp(w,s)$, but $R$ is defined by $R=\{r|\forall w\in W,Cmp(w,r\left)\right\}$. This means that $S\subseteq R$, which alongside $S\supseteq R$ gives us $S=R$.

This means that for all $V\in Ob\left(FV\right)$, $FGF\left(V\right)=F\left(V\right)$. We can skip writing $V$ and write this as $FGF=F$, which is also the same as saying that $FG=I$ (the identity morphism) on the image of $FV$ under $F$. Conversely $GF=I$ on the image of $CSB$ under $G$.

This also means that $(GF{)}^n=GF\forall n\in N_{+}$ so $GF$ is a "projection" operator. It "projects" the elements of $FV$ onto a subcategory of $FV$, but then doesn't do anything further to elements that are already there. Likewise for $FG$. 

On our earlier diagram this all looks like this:

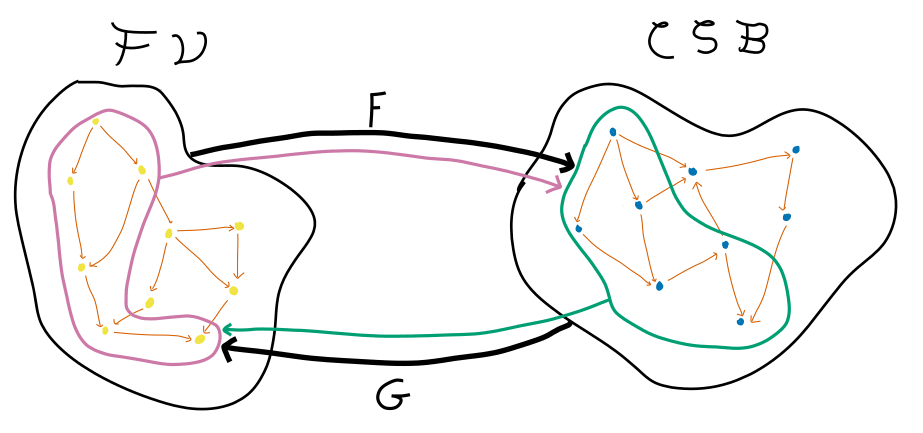
$F$ maps elements of $FV$ to a elements of $CSB$. We can label all of the elements that get "hit" as the image of $F$, written $Im\left(F\right)$. Likewise $G$ maps elements of $CSB$ to elements of $FV$, giving its image $Im\left(G\right)$. More importantly, $Im\left(G\right)\equiv Im\left(F\right)$, with $F=G^{-1}$ on these subcategories.

Properties of the Resulting Subcategories

In category theory, we tend not to care about what the elements of a category are, only about the structure present in the morphisms. Therefore, rather than consider the rather clunky concept of two equivalent subcategories which are formed as the images of functors, we really just want to look at the resulting structure. Since I have no idea what to call it, I will call these categories $D_n$ for now. Since it makes no sense to perform inference on zero variables, we'll impose the limit $n>0$.

$D_1\equiv 1$, which is the trivial category, with one element and one morphism. $D_2$ is a two element category with a morphism from one of its elements to the other. $D_3$ is a fifteen-element category with the structure discussed in the previous post.

$D_4$ has 1218 elements. This is the highest I've been able to enumerate using inefficient python code and a mediocre PC. I could perhaps try to get something to work on $D_5$, but no amount of efficiency can fight $O\left(2^{2^n}\right)$ for long. OEIS has nothing for the sequence 1,2,15,1218 so I'm stumped for better representations.

Combining Nodes in Bayes Nets

One bookkeeping rule we have not used yet is the node-combining rule. This lets us map an object of ${DAG}_n$ to an object of ${DAG}_{n-1}$. We do this by combining two numbers $i\ne j\in \{1,...,n\}$, replacing every $j$ in an edge with $i$, and then relabelling our numbers to be $\{1,...,n-1\}$. We can also do the same for ${FV}_n$, mapping its elements to ${FV}_{n-1}$. This also works by combining two numbers as above.

For a given set $X$ of possible "worlds", we might want to split it up into various partitions $X_i$ (unlike in FFS, we do not impose any restrictions on these partitions). So if we have $X\in \{a,b,c,d\}$ then the partition $X_1\in \{a,b\vee c\vee d\}$ is a totally valid variable, as is $X_2\{a\vee b,c\vee d\}$. These "naturally" give a new variable $(X_1,X_2)=\{a,b,c\vee d\}$ when combined.

So, given a copy of ${DAG}_n$, we can "join" two variables together to map each element to an element of a copy of ${DAG}_{n-1}$. We can do this in ${}^n{C}_2$ different ways. Up to now, we haven't really cared about what each node of a Bayes net actually was, but if we want to combine nodes we'll need to think about this. 

For a given set, $X$ and a set of set of partitions $X_i$, we can define ${DAG}_{\left\{X_i\right\}}$ as the category of Bayes nets over those partitions. We can then "glue together" all categories like this, to create ${DAG}_X$ for a set $X$. We can likewise associate factor overlap diagrams with these, and create ${FV}_{\left\{X_i\right\}}$ for each set of disjoint partitions. By gluing together the relevant functors $F$ and $G$ for each pair of categories, we can make an enormous category $D_X$ corresponding to all sets of Bayes nets that a probability distribution over $D_X$ could obey.

Three Further Thoughts

Thought 1

What are the properties of the sets in $GF\left(FV\right)$, i.e. the ones post-projection? Given a set of $m$ factor overlaps (which includes $\left\{\right\},\left\{1\right\},...,\left\{n\right\}$), can we determine in some reasonable time (polynomial in $m$ and $n$ perhaps?) whether it is changed by $GF$? We have no good closed-form representation of the elements of $D$ yet.

Thought 2

Bayes nets let us combine nodes (i.e. partitions) to get a new node and shrink the Bayes net, but is there some way to think about "blending" nodes continuously to move between Bayes nets with the same number of nodes?

So if we have our world $X\in \{a,b,c,d\}$, then we can split this into two nodes in a two-element Bayes net: $X_1\in \{a\vee b,c\vee d\},X_2\in \{a\vee c,b\vee d\}$. Or we could split it into two nodes like this: $X_1\in \{a\vee b,c\vee d\},X_3\in \{a\vee d,b\vee c\}$. Is there a way to embed these into a continuous space? Can we rotate between them? Can we describe probability distributions as elements of some space like $P\left(C^n\right)$ or something, then Bayes nets as regions in this space?

Thought 3

$D_X$ is unfathomably large even for small sets: we can have up to $Bell\left(n\right)$ different partitions (and $Bell\left(n\right)$ grows exponentially fast), so we may have up to $2^{Bell\left(n\right)}$ different Bayes nets, with the largest being