Suppose we have a bunch of earthquake sensors spread over an area. They are not perfectly reliable (in terms of either false positives or false negatives), but some are more reliable than others. How can we aggregate the sensor data to detect earthquakes?

A “naive” seismologist without any statistics background might try assigning different numerical scores to each sensor, roughly indicating how reliable their positive and negative results are, just based on the seismologist’s intuition. Sensor i gets a score $s_i^{+}$ when it’s going off, and $s_i^{-}$ when it’s not. Then, the seismologist can add up the $s_i^{+}$ scores for all sensors going off at a given time, plus the $s_i^{-}$ scores for sensors not going off, to get an aggregate “earthquake score”. Assuming the seismologist has decent intuitions for the sensors, this will probably work just fine.

It turns out that this procedure is equivalent to a Naive Bayes model.

Naive Bayes is a causal model in which there is some parameter $\theta$ in the environment which we want to know about - i.e. whether or not there’s an earthquake happening. We can’t observe $\theta$ directly, but we can measure it indirectly via some data $\left\{x_i\right\}$ - i.e. outputs from the earthquake sensors. The measurements may not be perfectly accurate, but their failures are at least independent - one sensor isn’t any more or less likely to be wrong when another sensor is wrong.

We can represent this picture with a causal diagram:

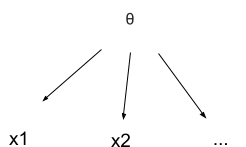
From the diagram, we can read off the model’s equation: $P[\theta ,\{x_i\left\}\right]=P\left[\theta \right]{\prod }_{i}P\left[x_i|\theta \right]$. We’re interested mainly in the posterior probability $P\left[\theta |\right\{x_i\left\}\right]=\frac{1}{Z}P\left[\theta \right]{\prod }_{i}P\left[x_i|\theta \right]$ or, in log odds form,

$L\left[\theta |\right\{x_i\left\}\right]=ln\frac{P\left[\theta \right]}{P[\sim \theta ]}+{\sum }_{i}ln\frac{P\left[x_i|\theta \right]}{P[x_i|\sim \theta ]}$

Stare at that equation, and it’s not hard to see how the seismologist’s procedure turns into a Naive Bayes model: the seismologist’s intuitive scores for each sensor correspond to the “evidence” from the sensor $ln\frac{P\left[x_i|\theta \right]}{P[x_i|\sim \theta ]}$. The “earthquake score” then corresponds to the posterior log odds of an earthquake. The seismologist has unwittingly adopted a statistical model. Note that this is still true regardless of whether the scores used are well-calibrated or whether the assumptions of the model hold - the seismologist is implicitly using this model, and whether the model is correct is an entirely separate question.

The Embedded Naive Bayes Equation

Let’s formalize this a bit.

We have some system which takes in data $x$, computes some stuff, and spits out some $f\left(x\right)$. We want to know whether a Naive Bayes model is embedded in $f\left(x\right)$. Conceptually, we imagine that $f\left(x\right)$ parameterizes a probability distribution over some unobserved parameter $\theta$ - we’ll write $P[\theta ;f(x\left)\right]$, where the “;” is read as “parameterized by”. For instance, we could imagine a normal distribution over $\theta$, in which case $f\left(x\right)$ might be the mean and variance (or any encoding thereof) computed from our input data. In our earthquake example, $\theta$ is a binary variable, so $f\left(x\right)$ is just some encoding of the probability that $\theta =True$.

Now let’s write the actual equation defining an embedded Naive Bayes model. We assert that $P[\theta ;f(x\left)\right]$ is the same as $P\left[\theta |x\right]$ under the model, i.e.

$P[\theta ;f(x\left)\right]=P\left[\theta |x\right]=\frac{1}{Z}P\left[\theta \right]{\prod }_{i}P\left[x_i|\theta \right]$

We can transform to log odds form to get rid of the Z:

$L[\theta ;f(x\left)\right]=ln\frac{P\left[\theta \right]}{P[\sim \theta ]}+{\sum }_{i}ln\frac{P\left[x_i|\theta \right]}{P[x_i|\sim \theta ]}$

Let’s pause for a moment and go through that equation. We know the function $f\left(x\right)$, and we want the equation to hold for all values of $x$. $\theta$ is some hypothetical thing out in the environment - we don’t know what it corresponds to, we just hypothesize that the system is modelling something it can’t directly observe. As with $x$, we want the equation to hold for all values of $\theta$. The unknowns in the equation are the probability functions $P[\theta ;f(x\left)\right]$, $P\left[\theta \right]$ and $P\left[x_i|\theta \right]$. To make it clear what’s going on, let’s remove the probability notation for a moment, and just use functions $G$ and $\left\{g_i\right\}$, with $\theta$ written as a subscript:

$\forall \theta ,x:G_{\theta }\left(f\right(x\left)\right)=c_{\theta }+{\sum }_i{g}_{\theta i}\left(x_i\right)$

This is a functional equation: for each value of $\theta$, we want to find functions $G$, $\left\{g_i\right\}$, and a constant $c$ such that the equation holds for all possible $x$ values. The solutions $G$ and $\left\{g_i\right\}$ can then be decoded to give our probability functions $P[\theta ;f(x\left)\right]$ and $P\left[x_i|\theta \right]$, while $c$ can be decoded to give our prior $P\left[\theta \right]$. Each possible $\theta$-value corresponds to a different set of solutions $G_{\theta }$, $\left\{g_{\theta i}\right\}$, $c_{\theta }$.

This particular functional equation is a variant of Pexider’s equation; you can read all about it in Aczel’s Functional Equations and Their Applications, chapter 3. For our purposes, the most important point is: depending on the function $f$, the equation may or may not have a solution. In other words, there is a meaningful sense in which some functions $f\left(x\right)$ do embed a Naive Bayes model, and others do not. Our seismologist’s procedure does embed a Naive Bayes model: let $G$ be the identity function, $c$ be zero, and $g_i\left(x_i\right)=s_i^{x_i}$, and we have a solution to the embedding equation with $f\left(x\right)$ given by our seismologist’s add-all-the-scores calculation (although this is not the only solution). On the other hand, a procedure computing $f\left(x\right)=x_1^{x_2^{x_3}}$ for real-valued inputs $x_1$, $x_2$, $x_3$ would not embed a Naive Bayes model: with this $f\left(x\right)$, the embedding equation would not have any solutions.