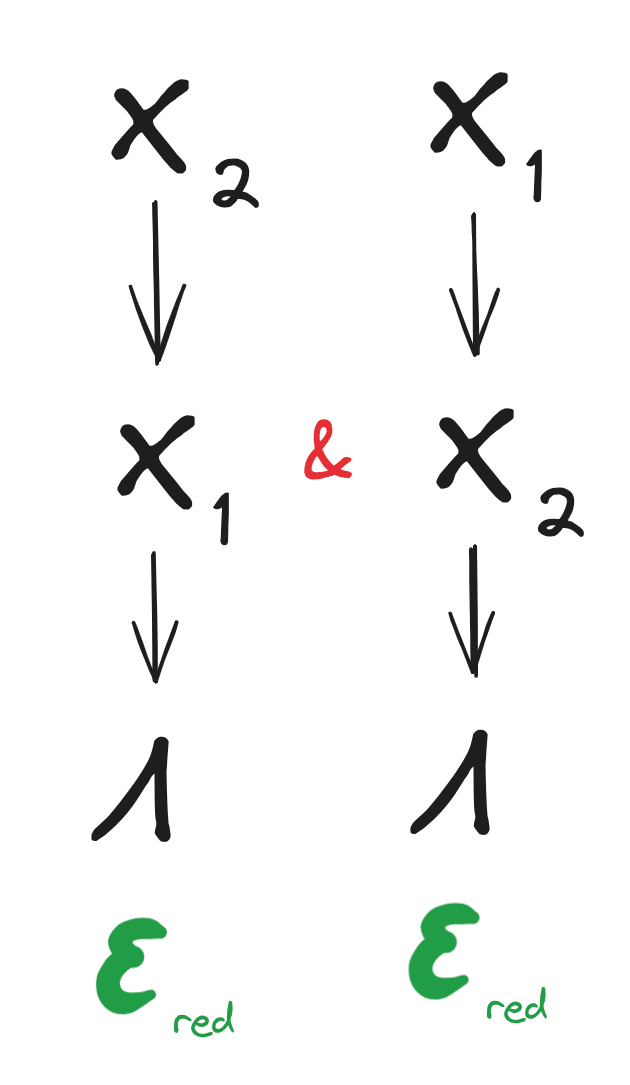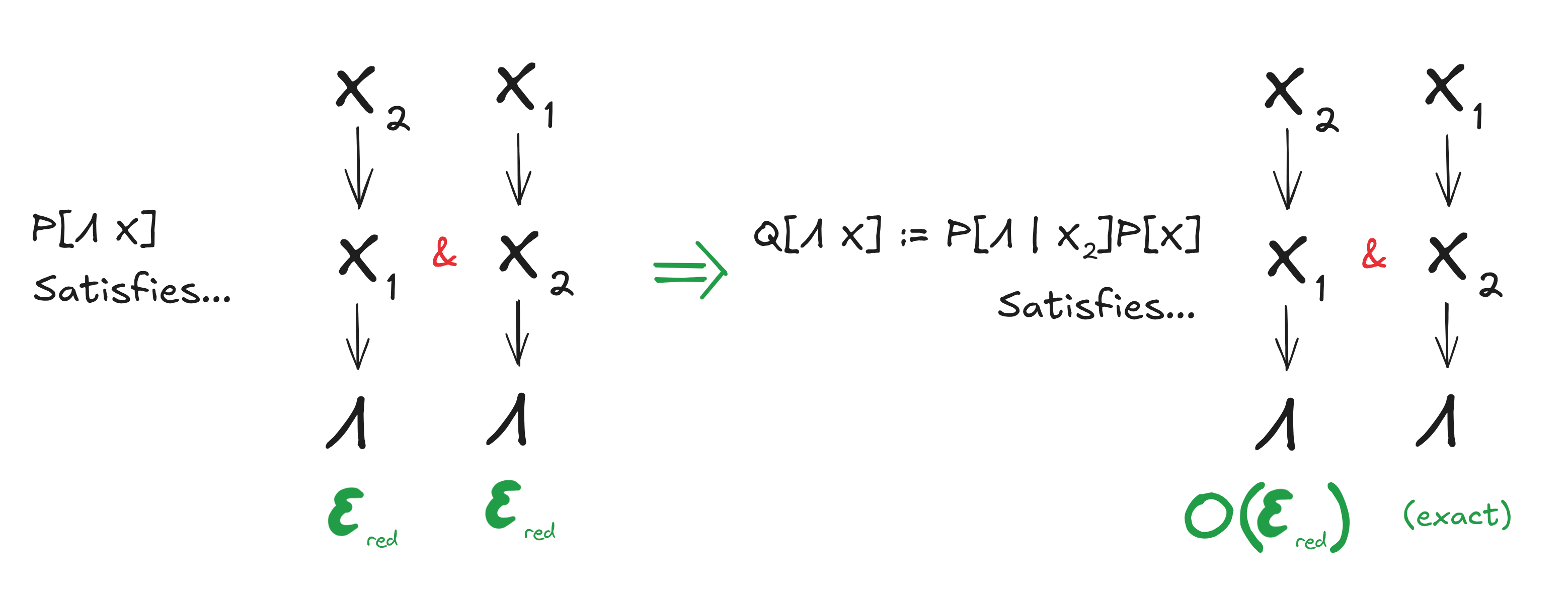Resampling Conserves Redundancy (Approximately)

David Lorell

Alfred Harwood and I were working through this as part of a Dovetail project and unfortunately I think we’ve found a mistake. The Taylor expansion in Step 2 has the 3rd order term . This term should disappear as $δ [X]$ goes to zero, but this is only true if $\sqrt{P [X]}$ stays constant. The $Γ$ transformation in Part 1 reduces (most terms of) $P [X]$ and $Q [X]$ at the same rate, so $\sqrt{P [X]}$ decreases at the same rate as $δ [X]$ . So the 2nd order approximation isn’t valid.

For example, we could consider two binary random variables with probability distributions

$P (x = 0) = z p$ and $P (X = 1) = 1 - z p$ and $Q (X = 0) = z q$ and $Q (X = 1) = 1 - z q$ .

If $δ [X] = \sqrt{P (X)} - \sqrt{Q (X)}$ , then $δ [X] \to 0$ as $z \to 0$ .

But consider the third order term for $X = 0$ which is

$\frac{1}{3} (\frac{\sqrt{Q (0)} - \sqrt{P (0)}}{\sqrt{P (0)}})^{3} = \frac{1}{3} (\frac{\sqrt{z q} - \sqrt{z p}}{\sqrt{z p}})^{3} = \frac{1}{3} (\frac{\sqrt{q} - \sqrt{p}}{\sqrt{p}})^{3}$

This is a constant term which does not vanish as $z \to 0$ .

We found a counterexample to the whole theorem (which is what led to us finding this mistake), which has $\frac{K L (X_{2} \to X_{1} \to Λ^{'})}{max [K L (X_{1} \to X_{2} \to Λ), K L (X_{2} \to X_{1} \to Λ)]} > 10$ , and it can be found in this colab. There are some stronger counterexamples at the bottom as well. We used sympy because we were getting occasional floating point errors with numpy.

Sorry to bring bad news! We’re going to keep working on this over the next 7 weeks, so hopefully we’ll find a way to prove a looser bound. Please let us know if you find one before us!

[-]johnswentworth1mo102

I plan to spend today digging into this, and will leave updates under this comment as I check things.

[-]johnswentworth1mo90

(Update 0)

I'm starting by checking that there's actually a counterexample here. We also found some numerical counterexamples which were qualitatively similar (i.e. approximately-all of the weight was on one outcome), but thought it was just numerical error. Kudos for busting out the sympy and actually checking it.

Looking at the math on that third-order issue... note that the whole expansion is multiplied by . So even if $δ [X] \sim \sqrt{P [X]}$ , $P [X]$ itself will still go to zero for small $δ$ , so $P [X] (\frac{δ [X]}{\sqrt{P [X]}})^{3}$ will go to zero. So it's not obviously a fatal flaw, though at the very least some more careful accounting would be needed at that step to make sure everything converges.

[-]David Lorell1mo150

(Update 1)

We've looked at the code and fiddled with the math and are now more convinced of the issue.

The 2nd order approximation holds when ...Which our scaling-down construction does not provide. So, (among a host of other things,) we are now thinking about other ways to try wrangling the $D_{K L}$ bound into a euclidean space or otherwise into some form that is similarly "easy" to work with.

(Thanks for finding this!)

[-]David Lorell1mo110

(Update 2)

Taking the limit of the ratio of s (using summation rather than max) with $c \to 0$ while $b := 10 c$ gives $5 (\frac{r + 1}{11})$

Setting c very small and ramping up r indeed brakes the bound more and more severely. (Code changes from the collab you provided, below.)

Code changes / additions

Block 1:
a,b,c,d,r = sp.symbols("a b c d r")
variable_substitutions = { # The definitions of these variables
a: 0.25,
b: 1e-90,
c: 1e-91,
r: 20000000,
}

Block 2 (later on):
expr = (kl3/(kl1 + kl2)).subs(d, (1-3*c-(r+1)*b-2*a))
print("KL(X2->X1->L')/sum[KL(X1->X2->L),KL(X2->X1->L)]=",(kl3/(kl1 +kl2)).evalf(subs=variable_substitutions))

Block3 (right after Block 2):
expr = (kl3/(kl1 + kl2)).subs(d, (1-3*c-(r+1)*b-2*a)).subs(b, 10*c)
lim = sp.simplify(sp.limit(expr, c, 0))
print("Limit of KL(X2->X1->L')/sum[KL(X1->X2->L),KL(X2->X1->L)] as c->0+ =", lim)

[-]johnswentworth1mo130

(Update 3)

We're now pursuing two main threads here.

One thread is to simplify the counterexamples into something more intuitively-understandable, mainly hopes of getting an intuitive sense for whatever phenomenon is going on with the counterexamples. Then we'd build new theory specifically around that phenomenon.

The other thread is to go back to first principles and think about entirely different operationalizations of the things we're trying to do here, e.g. not using diagram 's as our core tool for approximation. The main hope there is that maybe $D_{K L}$ isn't really the right error metric for latents, but then we need to figure out a principled story which fully determines some other error metric.

Either way, we're now >80% that this is a fundamental and fatal flaw for a pretty big chunk of our theory.

[-]johnswentworth24d110

(Update 4)

We have now started referring to "Jeremy et Al" when discussing the findings at top-of-thread, and find this amusing.

As of this morning, our current thread is an adjustment to the error measure. Thinking it through from first principles, it makes intuitive sense to marginalize out latents inside a , i.e. $D_{K L} (P [X] | | \sum_{Λ} Q [X, Λ])$ rather than $D_{K L} (P [X, Λ] | | Q [X, Λ])$ (where $Q$ is typically some factorization of $P [X, Λ]$ ). Conceptually, that would mean always grounding out errors in terms of predictions on observables, not on mind-internal latent constructs. We're now checking whether that new error gives us the properties we want in order to make the error measure useful (and in the process, we're noticing what properties we want in order for the error measure to be useful, and making those more explicit than we had before).

[-]David Lorell23d90

(Update 5)

A conjecture we are working on which we expect to be generally useful beyond possibly rescuing the stoch->det proof that used to rely on the work in this post:

Chainability (Conjecture):
with $ϵ_{1} := D_{K L} (X_{1} \to X_{2} \to Λ)$ , $ϵ_{2} := D_{K L} (X_{1} \leftarrow Λ \to X_{2})$ ,
Define $Q [X, Λ] := P [X] P [Λ | X_{2}]$ , and $Q^{'} [X, Λ] := Q [X_{1} | Λ] Q [X_{2} | Λ] Q [Λ]$ .
Then, $D_{K L} (P | | Q) < n (ϵ_{1} + ϵ_{2})$

Here is a collab with a quick numerical test that suggests the bound holds (and that n=1, in this case).

(Note: The above as written is just one step of chaining, and ultimately we are hoping to show it holds for arbitrarily many steps, accumulating an associated number of epsilons as error.)

[-]johnswentworth22d100

(Update 6)

Most general version of the chainability conjecture (for arbitrary graphs) has now been falsified numerically by David, but the version specific to the DAGs we need (i.e. the redundancy conditions, or one redundancy and the mediation condition) still looks good.

Most likely proof structure would use this lemma:

Lemma

Let be nonexpansive maps under distance metric $D$ . (Nonexpansive maps are the non-strict version of contraction maps.)

By the nonexpansive map property, $D (x, f_{1} (x)) \geq D (f_{2} (x), f_{2} (f_{1} (x)))$ . And by the triangle inequality for the distance metric, $D (x, f_{2} (f_{1} (x))) \leq D (x, f_{2} (x)) + D (f_{2} (x), f_{2} (f_{1} (x)))$ . Put those two together, and we get

$D (x, f_{2} (f_{1} (x))) \leq D (x, f_{1} (x)) + D (x, f_{2} (x))$

(Note: this is a quick-and-dirty comment so I didn't draw a nice picture, but this lemma is easiest to understand by drawing the picture with the four points and distances between them.)

I think that lemma basically captures my intuitive mental picture for how the chainability conjecture "should" work, for the classes of DAGs on which it works at all. Each DAG $j$ would correspond to one of the functions $f_{j}$ . where $f_{j}$ takes in a distribution and returns the distribution factored over the DAG $j$ , i.e.

$f_{j} (X \mapsto P [X]) := (X \mapsto \prod_{i} P [X_{i} | X_{p a^{j} (i)}])$

In order to apply the lemma to get our desired theorem, we then need to find a distance metric which:

Is a distance metric (in particular, it must satisfy the triangle inequality, unlike $D_{K L}$ )
Makes our DAG functions nonexpansive mappings
Matches $D_{K L} (P, f_{j} (P))$ AT THE SPECIFIC POINT P (not necessarily anywhere else)

The first two of those are pretty easy to satisfy for the redundancy condition DAGs: those two DAG operators are convex combinations, so good ol' Euclidean distance on the distributions should work fine. Making it match $D_{K L}$ at $P$ is trickier, still working that out.

[-]David Lorell18d100

(Update 7)

After some back and forth last night with an LLM^[1], we now have a proof of "chainability" for the redundancy diagrams in particular. (And have some hope that this will be most of what we need to rescue the stochastic->deterministic nat lat proof.)

(Theorem) Chainability of Redunds

Let P be a distribution over , $X_{2}$ , and $Λ$ .
Define:
$Q [X, Λ] := P [X] P [Λ | X_{1}]$
$S [X, Λ] := P [X] P [Λ | X_{2}] = P [X] \sum_{X_{1}} P [X_{1} | X_{2}] P [Λ | X]$ $R [X, Λ] := P [X] Q [Λ | X_{2}] = P [X] \sum_{X_{1}} P [X_{1} | X_{2}] P [Λ | X_{1}]$

Where you can think of Q as 'forcing' P into factorizing per one redundancy pattern: $X_{2} \to X_{1} \to Λ$ , S as forcing the other pattern: $X_{1} \to X_{2} \to Λ$ , and R as forcing one after the other: first $X_{2} \to X_{1} \to Λ$ , and then $X_{1} \to X_{2} \to Λ$ .

The theorem states,
$D_{K L} (P | | R) \leq D_{K L} (P | | Q) + D_{K L} (P | | S)$ ,

Or in words: The error (in $D_{K L}$ from $P$ ) accrued by applying both factorizations to P, is bounded by the the sum of the errors accrued by applying each of the factorizations to P, separately.

Proof

The proof proceeds in 3 steps.

$D_{K L} (P | | Q) \geq D_{K L} (S | | R)$
Pf.
Let $a_{X_{1}} := P [X_{1} | X_{2}] P [Λ | X] \geq 0$
Let $b_{X_{1}} := P [X_{1} | X_{2}] P [Λ | X_{1}] \geq 0$
By the log-sum inequality:
$\sum_{X_{1}} (a_{X_{1}} l n \frac{a_{X_{1}}}{b_{X_{1}}}) \geq (\sum_{X_{1}} a_{X_{1}}) l n (\frac{\sum_{X_{1}} a_{X_{1}}}{\sum_{X_{1}} b_{X_{1}}})$
$⟹$ $D_{K L} (P | | Q) \geq D_{K L} (S | | R)$ as desired.
$D_{K L} (P | | R) = D_{K L} (P | | S) + D_{K L} (S | | R)$
Pf.
$D_{K L} (P | | R) - D_{K L} (P | | S)$
$= \sum_{X, Λ} P [X, Λ] [l n P [Λ | X] - l n R [Λ | X_{2}] - l n P [Λ | X] + l n S [Λ | X_{2}]]$
$= \sum_{X_{2}} P [X_{2}] \sum_{Λ} \sum_{X_{1}} P [X_{1} | X_{2}] P [Λ | X] l n \frac{S [Λ | X_{2}]}{R [Λ | X_{2}]}$
$= \sum_{X_{1}} \sum_{X_{2}} P [X_{1} | X_{2}] P [X_{2}] \sum_{Λ} S [Λ | X_{2}] l n \frac{S [Λ | X_{2}] P [X]}{R [Λ | X_{2}] P [X]}$
$= D_{K L} (S | | R)$
Combining steps 1 and 2,
$D_{K L} (P | | Q) \geq D_{K L} (S | | R) = D_{K L} (P | | R) - D_{K L} (P | | S)$
$⟹ D_{K L} (P | | R) \leq D_{K L} (P | | Q) + D_{K L} (P | | S)$
which completes the proof.

Notes:
In the second to last line of step 2, the expectation over $P [X_{1} | X_{2}]$ is allowed because there are no free $X_{1}$ 's in the expression. Then, this aggregates into an expectation over $S [X, Λ]$ as $S [Λ | X_{2}] = S [Λ | X]$ .

We are hopeful that this, thought different than the invalidated result in the top level post, will be an important step to rescuing the stochastic natural latent => deterministic natural latent result.

^{^}
A (small) positive update for me on their usefulness to my workflow!

[-]johnswentworth18d80

Additional note which might be relevant later: we can also get proof step 1 in a somewhat more general way, which establishes that the function is a nonexpansive map under $D_{K L}$ . We'll write that proof down later if we need it.

[-]Jeremy Gillen24d50

our current thread is an adjustment to the error measure.

We're not sure that this is necessary. I quite like the current form of the errors. I've spent much of the past week searching for counterexamples to the ∃ deterministic latent theorem and I haven't found anything yet (although it's partially a manual search). My current approach takes a P(X_1,X_2) distribution, finds a minimal stochastic NL, then finds a minimal deterministic NL. The deterministic error has always been within a factor of 2 of the stochastic error. So currently we're expecting the theorem can be rescued.

rather than $D_{K L} (P [X, Λ] | | Q [X, Λ])$

That seems like a cool idea for the mediation condition, but Isn't it trivial for the redundancy conditions?

[-]johnswentworth23d20

That seems like a cool idea for the mediation condition, but Isn't it trivial for the redundancy conditions?

Indeed, that specific form doesn't work for the redundancy conditions. We've been fiddling with it.

[-]Daniel C24d30

Would this still give us guarantees on the conditional distribution ?

E.g. Mediation: $D_{K L} (P (X_{1}, X_{2}, Λ) ∥ P (X_{1} | Λ) P (X_{2} | Λ) P (Λ))$ $= D_{K L} (P (X_{1}, X_{2} | Λ) P (Λ) ∥ P (X_{1} | Λ) P (X_{2} | Λ) P (Λ))$ $= D_{K L} (P (X_{1}, X_{2} | Λ) ∥ P (X_{1} | Λ) P (X_{2} | Λ))$

is really about the expected error conditional on individual values of $Λ$ , & it seems like there are distributions with high mediation error but low error when the latent is marginalized inside $D_{K L}$ , which could be load-bearing when the agents cast out predictions on observables after updating on $Λ$

[-]Jeremy Gillen1mo90

Oh nice, we tried to wrangle that counterexample into a simple expression but didn't get there. So that rules out a looser bound under these assumptions, that's good to know.

[-]Jeremy Gillen1mo110

but thought it was just numerical error

I was totally convinced it was a numerical error. I spent a full day trying to trace it in my numpy code before I started to reconsider. At that point we'd worked through the proof carefully and felt confident of every step. But we needed to work out what was going on because we wanted empirical support for a tighter bound before we tried to improve the proof.

[-]David Lorell1mo60

Do you have sympy code for the example noted at the bottom of the collab that claims a ratio of > 9.77 including the mediation ? I tried with the parameters you mention and am getting a ratio of ~3.4 (which is still a violation of previous expectations, tbc.)

[-]Jeremy Gillen1mo70

That'll be the difference between max and sum in the denominator. If you use sum it's 3.39.

Here's one we worked out last night, where the ratio goes to infinity.

[-]Jeremy Gillen5d40

By the way, there seems to be an issue where sympy silently drops precision under some circumstances. Definitely a bug. A couple of times it's caused non-trivial errors in my KLs. It's pretty rare, but I don't know any way to completely avoid it. Thinking of switching to a different library.

[-]Jeremy Gillen2mo60

Part 1 feels like magic. I don't understand it at an intuitive level and so I'm kinda suspicious of it. It seems like such a powerful technique for working with KL divergences. I'll spend some more time playing around with it. Everything else makes sense to me.

My question is how did you come up with this technique? Was "small KL inequalities can be equivalent to larger KL inequalities" a background fact that you knew beforehand? Or did you start by wanting to find a way to make the Hellinger distances work?

[-]johnswentworth2mo80

It sure does feel like a powerful technique! We haven't explored much how to generalize it yet, though.

At the time, we were thinking about the optimization problem "max (the one error) subject to (constraint on other errors)", and what the curve looks like which gives the max value as a function of the constraint errors. One (of many) angles I tried was to consider ways of transforming a latent, which would move it from one point in the feasible set to another point in the feasible set. And once I asked that question, basically the first thing I tried was the transformation in the proof which just scales down all the errors.

At that point we had already done the Hellinger distances thing (also among many other things), on the general principle of "try it in the second order regime before trying to prove globally", so it was just a matter of connecting the pieces together.

LESSWRONG
LW

LESSWRONG
LW

66

Resampling Conserves Redundancy (Approximately)

66

Ω 27

66

Ω 27

(Theorem) Chainability of Redunds

Proof