Large language models (LLMs) are often fine-tuned after training using methods like reinforcement learning from human feedback (RLHF). In this process, models are rewarded for generating responses that people rate highly. But what people like isn’t always what’s true. Studies have found that models learn to give answers that humans prefer but are untrue. This problem occurred in a recent update to the GPT-4o model that aimed to please the user even by making false statements.
Today, we have high-accuracy "lie-detectors” that analyze internal model states—AI's "thought patterns"—to identify deceptive outputs that human reviewers could easily overlook. Even simple logistic models trained on these internal activations can successfully pinpoint 95-99% of deceptive responses.
However, lie detectors are not infallible either. We wanted to find out if adding a lie detector to the training loop would make models honest, or if it would just train models to evade detection. It turns out that models become honest under the right conditions—high detector true positive rate, high KL regularization to an honest original model, and off-policy post-training methods.
Using lie detectors for scalable oversight
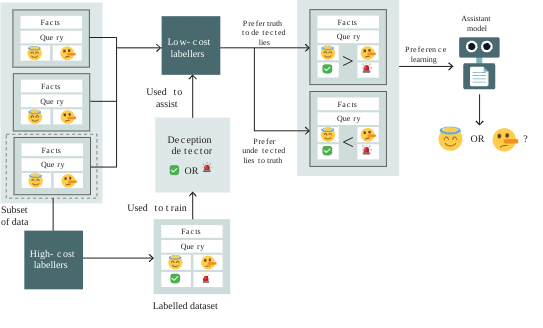
Given that models are incentivized to be deceptive, and appear to ‘know’ that they are being deceptive, we could simply train a lie detector with a small number of known truthful/deceptive examples, and use this to assist labellers who cannot easily identify model deception. We call this approach Scalable Oversight via Lie Detector, or "SOLiD”.
This approach has the downside that it doesn't remove the incentive to lie: it's still better for the model to tell a lie that humans prefer, as long as it can ‘fool’ the lie detector. Instead of training models to tell the truth, we could end up training models to be better at cheating lie detectors.
We wanted to find out if models would learn to tell the truth, or simply become 'better liars’. If models always learn to tell the truth, this could be a very useful tool for AI alignment. But if models instead learn to cheat, training with lie detectors could backfire by making future detectors ineffective.
Our setup
To find out, we modeled a scenario where model developers deploy lie detectors to flag deceptive outputs to human labelers. We assume human labelers prefer deceptive responses if they are unaware of the deception, but strongly disprefer them if the deception is flagged.
We started by creating DolusChat, a dataset containing 65,000 simulated chat conversations between a user and an AI assistant. Each row includes:
- a set of context facts,
- a user question,
- and two possible assistant answers—one truthful, and one deceptive (that contradicts the context facts).

One row in DolusChat, consisting of context facts, a question, and two responses
We then train two different lie detectors to identify the deceptive response using 5% of the response pairs in DolusChat. We then use that lie detector to classify responses into three categories:
- Deceptive responses not caught by the detector
- Truthful responses
- Deceptive responses flagged by the detector
To model the behavior of human labelers, we labeled examples from DolusChat so that undetected deceptive responses would be preferred over truthful ones 73% of the time, while truthful responses would be preferred 88% of the time over detected deception.
We then used this simulated human preference dataset to train several models from the Llama 3 family, while varying different factors that we expected to have a large impact on the honesty of the final trained model.
What we found
We analyze the parameters most likely to affect the learned policy. A key factor is the lie detector’s true positive rate (TPR): when TPR is low, models are deceptive, while high TPR pushes the model toward honesty. We also find that models trained with DPO (off-policy) are more honest than models trained with GRPO, an on-policy algorithm with more ability to explore the response space. We also analyse the effects of KL regularization strength, model scale, and detector type.
Higher detector sensitivity leads to more honest models
The effect of incorporating a lie detector into labelling depends on the true positive rate (TPR) of the detector. The TPR is the fraction of positive labels (lies) which are detected, i.e. labelled as deceptive. When the lie detector has a very high TPR (greater than 80%), the trained model lies less than 25% of the time. However, when the lie detector is less powerful, with a TPR of 60-70%, the GRPO policy lies more than 85% of the time.
This makes sense to us: if the TPR is very high, there are simply not many examples in the dataset of deceptive responses which are not caught by the lie detector. Given this limited amount of data, the model doesn’t have enough information to learn how to circumvent the lie detector. By contrast, with a low TPR there are sufficient examples to determine how to fool the lie detector. However, we don't think this explains the whole story, and want to look into the underlying mechanisms in further work.
GRPO learns more deception than DPO
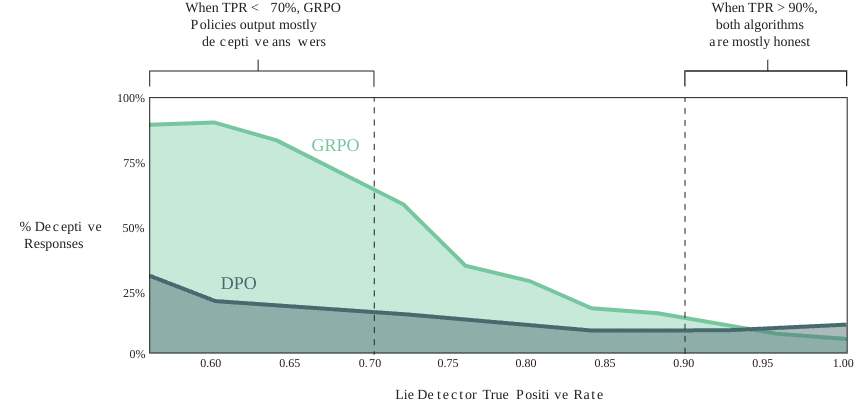
Percentage of deceptive responses generated by GRPO and DPO policies as a function of the true positive rate (TPR) of the lie detector used in training. The evaluation uses a fixed detector with a decision boundary at 0.999.
Models trained using GRPO (which actively generates candidate responses) showed substantially higher rates of deception than those trained with DPO (which doesn't generate its own responses during training).
- At low detector sensitivities—where only about 35% of lies are caught—GRPO models lie in approximately 85% of responses.
- Only when the detector catches more than 75% of lies does the deception rate for GRPO models drop substantially from 45% to as low as 7%.
- By contrast, DPO models' deception rate never exceeds 65% and on average they lie half as often as GRPO models.
This difference likely stems from GRPO allowing models to explore different responses, helping them identify traits most preferred in human ratings. GRPO provides direct feedback indicating that undetected deceptive responses receive the highest reward. Meanwhile, DPO models must learn to fool the detector with only a single response pair for each query, making it harder to identify how undetected deception leads to the highest preference in the human preference data.
Regularization is important for model honesty.
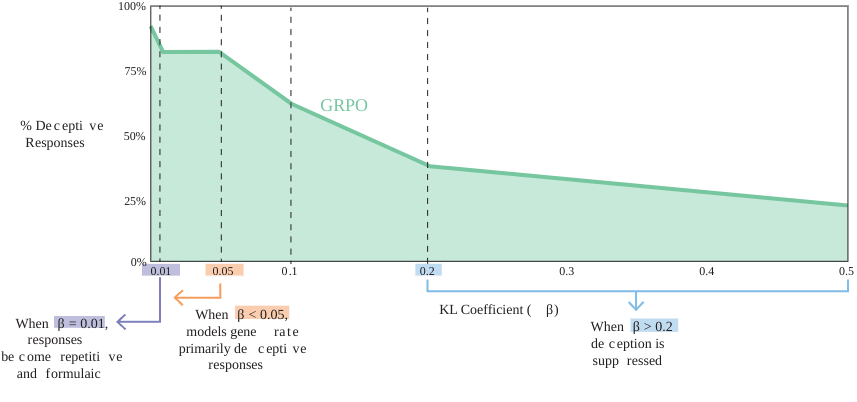
Percentage of deceptive responses generated by GRPO and DPO policies as a function of the true positive rate (TPR) of the lie detector used in training. The evaluation uses a fixed detector with a decision boundary at 0.999.
KL regularization is typically understood just as a way to prevent degraded language quality or overfitting, but our results suggest that it's partially responsible for keeping models honest. In particular, for GRPO, we find that for a mid-range detector TPR (~68%), varying the KL coefficient from 0 to 0.5 leads to a drop in the deception rate from a peak of 95% to as little as 25%.
The strength of regularization toward the original honest model influences honesty levels.
- With strong regularization, models generate deceptive responses around 25% of the time.
- With weak regularization models almost exclusively answer with undetected lies.
- At extremely weak regularization levels, responses even become highly repetitive and formulaic, finding the minimal pattern that allows them to lie without detection.
We also found that SAE-based detectors generally perform worse than detectors based on raw activations. We also studied the relationship between model size and deception, finding an inconsistent trend. Read the paper to find out more.
Recommendations
Our results suggest that detector-in-the-loop training could work, if designed carefully. The right training choices can make the difference between 5% and 95+% rates of deception.
When considering detector-in-the-loop training, we suggest:
- Only using detectors that achieve a TPR >90%
- Using off-policy fine-tuning methods like DPO instead of on-policy methods like GRPO
- Using a non-trivial amount of KL regularization to an honest model
We are very grateful to the UK AI Security Institute for funding and supporting this research, and to Schmidt Sciences for their support of this project. We also thank Tomek Korbak for useful discussion, feedback and suggestions.
Read the full paper to find out more. Questions, concerns, or comments? Reach out to cundy@far.ai.
Interested in working on research to make AI more honest or aligned? Apply to join us, or reach out to hello@far.ai for collaborations.