Introduction and Motivation

As part of the 5th iteration of the Arena AI safety research program we undertook a capstone project. For this project we ran a range of experiments on an encoder-decoder model, focusing on how information is stored in the bottleneck embedding and how modifying the input text or embedding impact the decoded text. Some of the findings are shown in this blog post, and the companion post by @Samuel Nellessen here. We helped each other throughout, but most of his work is documented in his post, and this post documents my findings. This work was also supported by @NickyP and was in part motivated by this. 

Although created for the purposes of language translation and not complex reasoning, studying this type of model is interesting for a few reasons:

• Maybe some of the behaviour of encoder-decoder models is also exhibited by LLMS in the residual stream. Might be vaguely helpful for AI safety.
• In order to do the translating (or decoding back into the same language), a lot of meaning has to be compressed into a small bottleneck. Maybe there are some interesting patterns in this embedding.
• Maybe some unexpected complex behaviour arises in these models.
• There hasn’t been much interpretability work into this kind of model, maybe there are some low hanging fruit here.
• The model encodes entire sequences of text into a single embedding vector which is very manageable to study.

The Model

META’s SONAR model is a multi-lingual text and speech encoder and text decoder model trained for translation and speech-to-text purposes. In this study we look only at the text encoding and decoding and ignore the multi-modal capabilities of the model. 

The model is composed of:

• The encoder: A 24-layer transformer encoder which outputs an encoding - a vector of size 1024 - for each token in the sequence.
• The embedding: The embeddings for each input token are pooled to create a single bottleneck embedding of size 1024 that encodes the entire input text.
• The decoder: A 24-layer transformer decoder which takes the bottleneck embedding as input and auto-regressively generates the output text. 

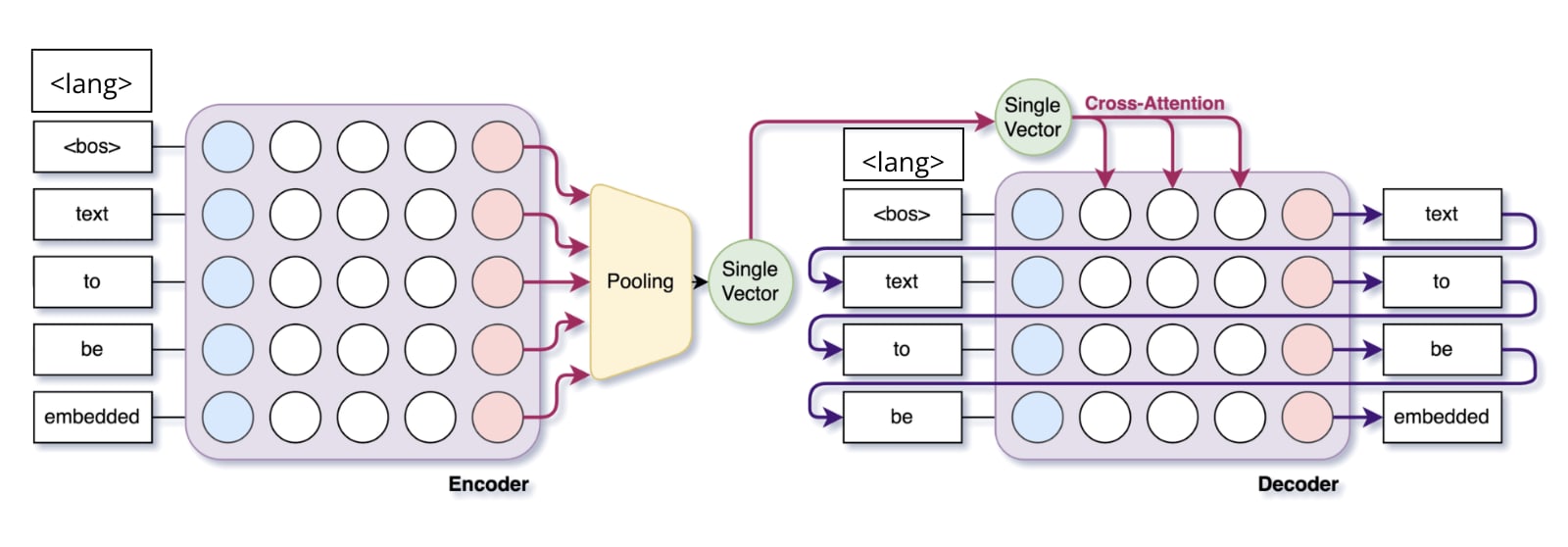
The encoder and decoder begin with a language token which is used by the model to properly store the information in the embedding, and to correctly translate the meaning of the input text into the target language.

Investigations

How Does the Input Language Impact the Bottleneck Embedding

Motivation

When encoding some text we begin the sequence with a language token to tell the encoder which language is being input, and when decoding we do the same to tell the decoder which language to generate the output in. In this way we can use the same model to encode/decode from/to any of the large choice of languages (see here).

An open question was to check how the input language of choice impacts the embedding, is the embedding language agnostic? We might expect one of the following:

• Since the decoder can take an embedding encoded from any language, and decode it to any language, that the semantic information stored in the embedding just stores the “meaning” of the text and not any information about the languages themselves (ignoring the case where the semantic meaning is language dependent, say for words that don’t have direct translations). In this case the decoder would take this embedding plus the target language token and generate the text based solely on that.
• The encoder does encode some information about the source language into the embedding. This could allow for the same sentences from different languages to be encoded differently, so that the decoder could then use that extra information about the source language to properly generate the translated text (remember that the decoder has no knowledge about the source language, only what it can get from the embedding). For example the embedding generated from English for “I’m a bit blue”, versus from Spanish “Estoy algo azul”, if we know the embedding came from English then the decoder could have more information to more accurately translate the text given the less literal meaning being sad. In other words, does the decoder do some of the work of mapping between the two languages, or is all of the information/meaning in the embedding language agnostic.
• Some more complex combination of the above two.

Experiment

For this experiment we take about 300 English sentences and their Spanish translations. We embed each of the samples, two embeddings each (one for each language). Using this we can then run a bunch of quick experiments. Throughout we refer to "English embedding" as an embedding generated from English input text, regardless of if that information is stored in the embedding (and similarly for "Spanish embedding"). Note that decoding an English embedding back in to English seems to always generate the same text word for word (and similarly for Spanish embeddings decoded into Spanish).

• For each pair of English-Spanish embeddings, decode them separately into the other language. Do the decoded sentences match the expected translation? Although not always guaranteed to be identical, the semantic meaning is very well preserved. This implies that even though there might be information loss when creating the embedding, it is not significant, or is small enough that the decoder can manage fine. In other words, the decoded sequence doesn't seem to be impacted by the language used when generating the embedding.
• What can we see by inspecting the embeddings themselves? We take all of the embeddings and look at how far each English embedding is from its Spanish embedding. The difference is small. The difference between any two random embeddings is always larger than between the embedding of the same sentence in different languages.
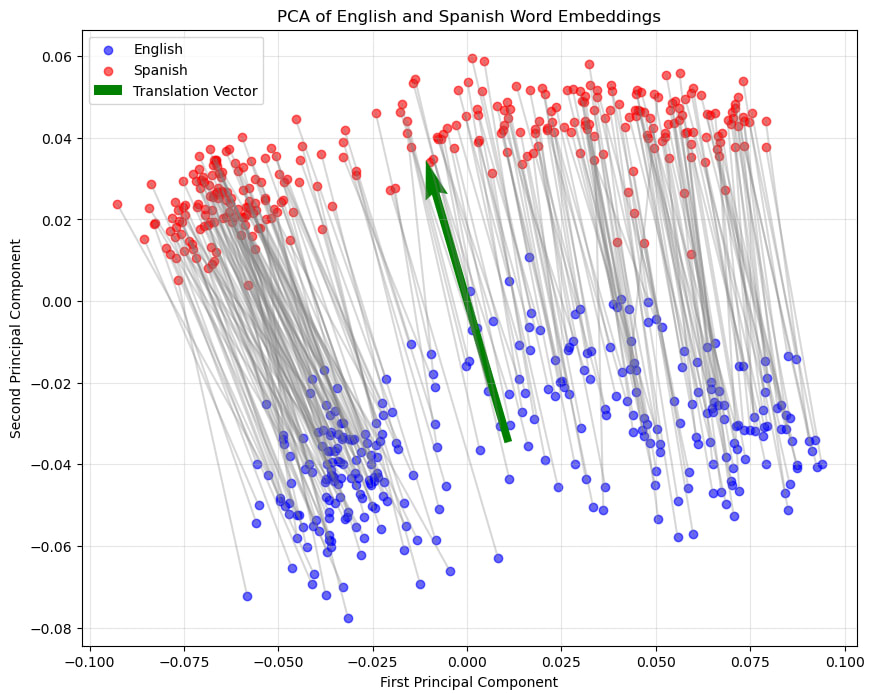
• By doing PCA we visualise all of the embeddings together. Note that most of the big differences are hidden here because most embeddings have large values in orthogonal directions. Here we can clearly see that the first principle component corresponds to something else, but the second principle component clearly separates the embeddings from each language. Although the difference is small, there is a clear divide. In other words, although the impact is small, the embedding does seem to encode information about what the source language was.
• Generally the vector pointing from any English embedding to its corresponding Spanish embedding is almost parallel and has almost the same magnitude as any other of these vectors. Seems like there is a clear English to Spanish vector.
• We can average these vectors to get a vector to convert any English embedding to be shifted to the Spanish area of the embedding space. Shifting any English embedding by this vector does indeed provide an embedding that is basically identical to the corresponding Spanish embedding.
• This shifting in embedding space has no impact on the decoded text.

Limitations and Further Work

This was a quick initial experiment that could do with deeper analysis. Some limitations and open questions:

• Is our English to Spanish vector truly that, or does it correspond to something else that is simply correlated with English to Spanish?
• We didn’t try different languages.
  • Would a third language be separated along a direction perpendicular to our English to Spanish vector? If there is a language that would cluster somewhere along the same vector as our English to Spanish vector then it would mean that it is not simply an English to Spanish vector after all.
  • Languages aren't necessarily binaries, would an English to Portuguese vector be similar to the English to Spanish vector. What about Scots to Spanish?
  • Similarly, given many languages lie on a continuum, are more similar languages closer together?
  • What would happen if we were to look at languages that are more different from each other. Would English vs Mandarin be way more separable? Would the translations used for input be more different in their inherent meaning (and embedding)? Would the population of individual English to Mandarin vectors be more noisy. Would we see a difference in the decoding (to English or to Mandarin) if we shifted the English embeddings along the general English to Mandarin direction?
• We tried quite short texts. Would be good to have been able to confirm our findings with longer texts, and more semantically complex texts.
• Only 300 samples is not really ideal.
• We relied on English and Spanish samples generated by an LLM. This most likely has generated texts from some population that has some specific style/topic/format that could well bias our results - they are probably not covering a wide range of possible texts.

Conclusion

It appears that the source language information is encoded in the bottleneck embedding, although why is unclear. It could be an artefact of the encoder that has no impact, or maybe it is useful for the decoder in situations that weren't covered by the examples we tested. The main takeaway is that the source language does impact the embedding, and that this information could be used by the decoder if needed.

How is Positional Information Stored in the Embedding

Motivation

Can we learn something about how positional information (token position in the input sequence) is encoded. Encoder-decoder models work well with semantically meaningful sequences, but they can also embed and decode other types of sequences. They must have some way of encoding a sequence in a way that differs from how they embed meaningful language. How do they do this? Can we manipulate the embedding to control the decoder's output sequence?

Experiment

To begin with, we visualise how positional information is stored. If we take a sequence like "dog _ _ _ _ _", we can encode it to get an embedding. Note that "dog" is a single token, as is the token used for filler "_", the spaces in the string are just for clarity and are not present in the input sequence. We can then shift the token for dog repeatedly to get input sequences "_ dog _ _ _ ", "_ _ dog _ _ _" etc. We then look at how the embeddings change as we shift the token along. Plotting the embeddings for about 20 positions with PCA we can see that the embedding vector appears draw out a circular pattern or an arc. The distance between subsequent embeddings gets smaller as the position of the token increases - this makes sense as for super long sequences you could imagine that the exact position matters less. 

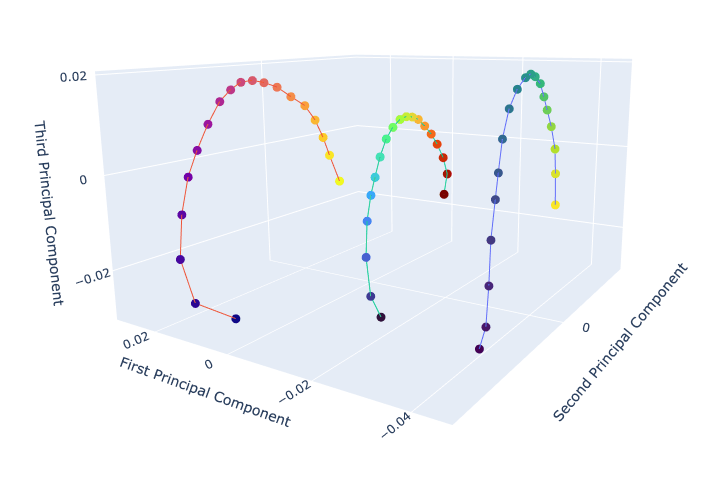
Note that decoding works perfectly for these kinds of sequences. Testing on super long sequences (say above 30 tokens) does begin to show some degradation, where the decoded token position is wrong, or we just get the filler token only.

We see a nice pattern here, can we get a general vector that we can use to tweak an embedding to control the decoded sequence? We take the embedding for "_ _ dog _ _ _", subtract from it the vector from the embedding from "_ dog _ _ _ _", which hopefully then is a vector that if added to an embedding, will shift token in the decoded sequence to the right by one. We indeed find that adding this to the embedding for "_ cat _ _ _ _" and decoding does in fact give "_ _ cat _ _ _".

These vectors are not so useful however because they only work if the filler tokens are the same, so are not useful for arbitrary sequences. In fact if we change the filler token, the pattern above completely changes. There appears to always be a path followed as we shift the tokens, and always arc-like, but they are always different. This means that there isn't an obvious general arbitrary way to control the token position.

Conclusion

We can in principle see a pattern to how positional information is encoded in the embedding, and it appears that earlier positions are more important that later ones. Although the vectors to shift token positions work, it is only in very specific situations and probably not useful. It is interesting that the embeddings aren't completely arbitrary, they can in principle be inspected. The fact that a vector shifting a token works for any other token wasn't known a priori. There is definitely more room here for experimentation.

Can we Manipulate the Embedding to Arbitrarily Change Tokens

Motivation

We want to investigate how is the information about particular input tokens stored. How cleanly is the information embedded. Is if possible to manipulate the embedding to have fine grained control on the decoded sequence?

Experiment

Here we look at changing a particular token in a sequence to another by manipulating the embedding. Can we manipulate the embedding of "dog a bit dog b" so that it decodes to "dog a bit cat b"?

We first try to do this by calculating the shifting vector by subtracting the embedding for  "_ _ _ dog _" from "_ _ _ cat _". If we add this vector to the embedding for "dog a bit dog b" we decode to "cat a bit cat b". This is interesting, by default we get a general "dog" to "cat" direction. Further experiments showed that indeed all instances of "dog" become "cat" regardless of the input sequence. The positional information here is ignored.

Instead if we do the same, but subtract "dog _ _ dog _" from "dog _ _ cat _", then this does in fact only change the token from "dog" to "cat" only for the "dog" in fourth position. For example we can apply this to "dog is happy dog now" to get "dog is happy cat now". We successfully leave the "dog" in the first position untouched. This tells us that we have captured more than just a meaning difference between "dog" and "cat" but also some positional information i.e. more evidence that positional information is stored in the embedding (as we can see in the previous section).

Interestingly this only works for grammatically correct sentences. If we try to do the same approach to change "dog a bit dog b" to "dog a apple dog b" (i.e. by subtracting the embedding for  "_ _ apple _ _" from "_ _ bit _ _" and adding it to the embedding from "dog a bit dog b") then it fails, it decodes to "dog a likes dog b". This implies that even though we can manipulate the embedding to change a token, and even a token at a given position, we are at the mercy of what the decoder does. It seems to have a preference for generating useful/valid text and doesn't want to put a noun where a verb should be.

Conclusion

We can:

• Get a general direction pointing from one type of token to another, which when applied to the embeddings causes the decoder to change all instances of the token. This tells us that there are regions of embedding space corresponding to particular concepts, as we see with the residual stream in LLMs.
• Do the same but applying the shift to tokens only in particular positions. Confirming the results above that positional information is stored in the embedding.
• We can't force any word to change. If the input token is within a valid sequence of tokens - valid English for example - then the decoding will prefer to decode a valid English sequence rather than our manipulated one.

Conclusions

For experiment specific conclusions see the conclusion sections for each of individual investigations above.

Quick summary:

• Decoding is robust, it doesn't matter which language was used as input.
• Decoding is robust, it can successfully decode arbitrary sequences (as long as they're not too long).
• Decoding is robust, it will tend to produce valid [language of your choice] text even if the embedding has been corrupted. The meaning of the sequence might be changed but it will be valid [language of your choice].
• The embedding doesn't only store semantic meaning:
  • There is information about the input language stored in the bottleneck embedding, although its purpose (if any) is unclear.
  • There is positional information stored in the embedding. Appears to be useful to help decoding. Definitely a necessity for decoding non-semantic sequences.

An overall result is that the bottleneck embedding appears to behave somewhat like the residual stream in LLMs in the sense that there seem to be orthogonal directions that carry semantic meaning. Due to this, along with their simplicity, studying these models could be useful for better understanding some LLM dynamics. 

We did a wide range of investigations to probe for interesting behaviour and interesting initial findings. Given the limited time we had, we didn't have time to dig deeper or rigorously prove our findings. Take my conclusions here with a grain of salt, I believe them to be the case based on my results, but they could just be rationalisations. This definitely could do with more work and I would be happy if someone would expand on this. For anyone interested, there is a utility class for working with the Sonar model and some scripts that you can steal from to get started on your own experiments.