(This is the fourth post in a series on Machine Learning based on this book. Click here for part one. If you have some background knowledge, this post might work as a stand-alone read.)

The mission statement for this post is simple: we wish to study the class of linear predictors. There are linear correlations out there one might wish to learn; also linear stuff tends to be both efficient and simple, so they may be a reasonable choice even if the real world is not quite linear. One can also build more sophisticated classifiers by using linear predictors as building blocks, but not in this post).

In school, a function is linear iff you can write it a $f (x) = a x + c$ . In higher math, a function $f : X \to Y$ is linear iff $f (x + y) = f (x) + f (y)$ for all $a, b \in X$ . In the the case of $f : R^{d} \to R$ , this condition holds iff $f$ it can be written as $f (x) = \sum_{i = 1}^{d} a_{i} x_{i}$ for some parameter vector $a \in R^{d}$ . So the requirement is stronger – we do not allow the constant term the school definition has – but one also considers higher dimensional cases. The case where we do allow a constant factor is called affine-linear, and we also say that a function is homogeneous iff , which (in the case of affine-linear functions) is true iff there is no nonzero constant factor.

In Machine Learning, the difference between linear and affine-linear is not as big of a deal as it is in other fields, so we speak of linear predictors while generally allowing the inhomogeneous case. Maybe Machine Learning is more like school than like university math ;)

For $X = R^{d}$ and some $Y \subseteq R$ , a class of linear predictors can be written like so:

L_{d, ϕ} = {h : x \mapsto ϕ (⟨ a, x ⟩ + c) | a \in R^{d}, c \in R}

Let's unpack this. Why do we have an inner-product ⟨⋅⟩ here? Well, because any function $f : x \mapsto \sum_{i = 1}^{d} a_{i} x_{i}$ can be equivalently written as $f : x \mapsto ⟨ a, x ⟩$ , where $a := (a_{1}, . . ., a_{d})$ . The inner-product notation is a bit more compact, so we will prefer it over writing a sum. Also note that, for this post, bold letters mean "this is a vector" while normal letters mean "this is a scalar". Secondly, what's up with the $ϕ$ ? Well, the reason here is that we want to catch a bunch of classes at once. There is the class of binary linear classifiers where $Y = {- 1, 1}$ but also the class of linear regression predictors where $Y = R$ . (Despite what this sequence has looked like thus far, Machine Learning is not just about binary classification.) We get both of them by changing $ϕ$ . Concretely, we get the linear regression functions by setting $ϕ = ϕ_{sign} := 1_{R_{+}} - 1_{R_{-}}$ , i.e., the function that sends all positive numbers to 1 and all negative numbers to $- 1$ . The notation $1_{M}$ for any set $M$ denotes the indicator function that sends all elements in $M$ to 1 and all others in its domain to 0.

For the sake of brevity, one wants to not write the constant term but still have it around, and to this end, one can equivalently write the class as

L_{n, ϕ} = {h : x \mapsto ϕ (⟨ a^{'}, x^{'} ⟩) | a^{'} \in R^{d + 1}}

where it is implicit that $x' = (x : 1)$ . Then, the final part of the inner product will add the term $a_{d + 1} \cdot x_{d + 1}^{'} = a_{d + 1} \cdot 1 = a_{d + 1}$ , so $a_{d + 1}$ will take on the role of c in the previous definition.

We still need to model how the environment generates points. For this section, we assume the simple setting of a probability function D over X only and a true function $f : X \to Y$ of the environment. We also need to define empirical loss functions for a training sequence $S \in (X \times Y)^{*}$ . For binary classification, we can use the usual one that assigns h the number $\frac{1}{| S |} | {(x, y) \in S | h (x) \neq y)} |$ . Since we will now look at more than one loss function, we will have to give it a more specific name than $ℓ_{S}$ , so we will refer to it as $ℓ_{S}^{0 - 1}$ , indicating that every element is either correctly or incorrectly classified. We call this the 0-1 loss even though the label set is now $Y = {- 1, 1}$ .

For regression (where $Y = R$ ), this is a poor function since hitting the precisely correct element in $R$ is not a reasonable expectation – and if 3.8 is the correct answer, then $3.8 + 10^{- 47}$ is a better guess than 17. Instead, we want to penalize the predictor based on how far it went off the mark. If $S = ((x_{1}, y_{1}), . . ., (x_{n}, y_{n}))$ , then we define the squared distance loss function as $ℓ_{S}^{(2)} (h) := \sum_{i = 1}^{n} (h (x_{i}) - y_{i})^{2}$ and the absolute distance loss function as $ℓ_{S}^{(1)} (h) := \sum_{i = 1}^{n} | h (x_{i}) - y_{i} |$ .

We begin with binary linear classification.

Binary Linear Classification

A binary linear classifier separates the entire space in two parts along a hyperplane. (A hyperplane in $R^{d}$ is a $d - 1$ dimensional subspace.) This is quite easy to visualize. In the homogeneous case, the hyperplane will go through the origin, whereas in the inhomogeneous case, it may not.

Let's work out why this is so. A point $x$ is sent to $ϕ (⟨ a^{'}, x^{'} ⟩)$ , do it gets classified positively iff $⟨ a^{'}, x^{'} ⟩$ is greater than 0. Suppose we're somewhere in the red area where this is not the case, and now we move into the direction of $a^{'}$ . At some point, we will be at a place where the inner product is exactly 0. Now, if we move into a direction orthogonal to $a^{'}$ , the inner product doesn't change. This corresponds to the hyperplane that is visualized in the pictures above.

In linear classification problems, we say that a problem is separable iff there exists a vector $a^{*}$ whose predictor gets all points in the training sequence right. In the book, this distinction is also frequently made for other learning tasks, where a problem is called realizable iff there exists a perfect predictor. For linear predictors, the space might be very high dimensional, which makes this assumption more plausible. As an example, suppose we model text documents as vectors, where there is one dimension for every possible term, and one sets the coordinate for the word "crepuscular" to the number of appearances of the word "crepuscular" in the document. With $\approx 171476$ dimensions at hand, it might not be so surprising if a hyperplane classifies all domain points perfectly.

How do we train a linear classifier? The book discusses two different algorithms. For both, we shall first assume that we are in the homogeneous case. We start with the Perceptron algorithm.

The Perceptron algorithm

Since our classifier is completely determined by the choice of $a$ , we will refer to it as $h_{a}$ . Thus $h_{a} (x) = ϕ_{sign} (⟨ a, x ⟩)$ .

Recall that ha measures how similar a label point is to a and classifies it as 1 if it's similar enough (and as $- 1$ otherwise). This leads to a very simple algorithm: we start with $a^{0} = 0$ ; then at iteration t we take some pair $(x, y)$ that is not classified correctly – i.e., where either $⟨ a^{t}, x ⟩ > 0$ even though $y = - 1$ or $⟨ a^{t}, x ⟩ < 0$ even though $y = 1$ – and we set $a^{t + 1} := a^{t} + y x$ . If $x$ was classified as $- 1$ even though $y = 1$ , then we add $x$ , thereby making $a^{t + 1}$ more similar to $x$ than $a^{t}$ , and if $x$ was classified as 1 even though $y = - 1$ , then we subtract $x$ , thereby making $a^{t + 1}$ less similar to $x$ than $a^{t}$ . In both cases, our classifier updates into the right direction. And that's it; that's the perceptron algorithm.

It's not obvious that this will ever terminate – while updating towards one point will make the predictor better about that point, it might make it worse about other points. However, there is a theorem stating that it does, in fact, terminate provided the problem is separable. The proof is partially interesting but also technical, so I'll present a sketch that includes the key ideas but hides some of the details.

The main idea is highly non-trivial. We assume there is no point directly on the separating hyperplane, then we begin by choosing a vector a∗ whose predictor classifies everything correctly (which exists because we assume the separable case) and also has scalar product at least 1 with every positive point (take one that satisfies the first condition and divide it by the smallest norm of any positively labelled point). Now we observe that the similarity between at and a∗ increases as t increases. This is so because $⟨ a^{t + 1}, a^{*} ⟩ = ⟨ a^{t} + y \cdot x, a^{*} ⟩ = ⟨ a^{t}, a^{*} ⟩ + y ⟨ x, a^{*} ⟩$ , and the term $y ⟨ x, a^{*} ⟩$ is positive since $a^{*}$ is by assumption such that $⟨ x, a^{*} ⟩ > 0 ⟺ y = 1$ . This shows that $⟨ a^{t}, a^{*} ⟩$ grows as t grows.

The proof then proceeds like this:

Establish a lower bound on the growth rate of $⟨ a^{t}, a^{*} ⟩$
Establish an upper bound on the growth rate of $| | a^{t} | |$
Observe that $| | a^{*} | |$ is a constant
Observe that $⟨ a_{t}, a^{*} ⟩ \leq | | a^{t} | | \cdot | | a^{*} | |$ must hold because it's the famous Cauchy-Schwartz inequality
Conclude that, as a consequence of the four facts above, the term t can only grow for a limited number of iterations

We obtain a bound that depends on the norm of the smallest vector $a^{*}$ such that $⟨ a^{*}, x ⟩ \geq 1$ for all domain points $x \in X$ and on the largest norm of any domain point. This bound might be good or it might not, depending on the case at hand. Of course, the algorithm may always finish much earlier than the bound suggests.

Linear Programming

Linear programming is an oddly chosen name for a problem of the following form:

max x \in R^{d} ⟨ u, x ⟩ s.t. A x \geq b

where $u \in R^{d}$ and $b \in R^{n}$ and $R^{n, d}$ are given. So we have a particular direction, given by $u$ , and we want to go as far into this direction as possible; however, we are restricted by a set of constraints – namely the $n$ many constraints that follow from the equation $A x \geq b$ . Each constraint is much like the predictor $h$ from the previous section; it divides the entire space $R^{d}$ into two parts along a hyperplane, and it only accepts points in one of the two halves. The set of points which are accepted by all constraints is called the feasible region, and the objective is to find the point in the feasible region that is farthest in the direction of u.

Here is a visualization for d=2 and n=3:

Once we hit the triangle's right side, we cannot go any further in precisely the direction of u, but going downward along that side is still worth it, because it's still "kind of" like u – or to be precise, if $w$ is the vector leading downward along the rightmost side of the triangle, then $⟨ u, w ⟩ > 0$ , and therefore points which lie further in this direction have a larger inner product with $u$ . Consequently, the solution to the linear program is at the triangle's bottom-right corner.

The claim is now that finding a perfect predictor for a separable linear binary classification problem can be solved by a linear program. Why is this? Well for one, it needs to correctly classify some number of points, let's say $n$ , so it needs to fulfil $n$ conditions, which sounds similar to meeting $n$ constraints. But we can be much more precise. So far, we have thought of the element $a$ that determines the classifier as a vector and of all domain elements as points, but actually they are the same kind of element in the language of set theory. Thus, we can alternatively think of each domain element $x \in X$ as a vector and of our element a determining the classifier as a point. Under this perspective, each $x \in X$ splits the space in two halves along its own hyperplane, and the point a needs to lie in the correct half for all $n$ hyperplanes) for it to classify all $x$ 's correctly. In other words, each $x \in X$ behaves exactly like a linear constraint.

Thus, if $S = ((x_{1}, y_{1}), . . ., (x_{n}, y_{n}))$ , then we can formulate our set of constraints as $X a \geq 1$ (not ≥0 because we want to avoid points on the hyperplane), where

$X = ⎡ ⎢ ⎢ ⎣ \begin{matrix} y_{i} x_{1} ⋮ y_{n} x_{n} \end{matrix} ⎤ ⎥ ⎥ ⎦$

i.e. the matrix whose row vectors are either the elements $x_{i}$ (if $y_{i} = 1$ ) or the elements $x_{i}$ scaled by $- 1$ (if $y_{i} = - 1$ ). The $i$ -th coordinate of the vector $X a$ equals precisely $y_{i} ⟨ x_{i}, a ⟩$ , and this is the term which is positive iff the point is classified correctly, because then $⟨ x_{i}, a ⟩$ has the same sign as $y_{i}$ .

We don't actually care where in the feasible region we land, so we can simply set some kind of meaningless direction like $u = 0$ .

So we can indeed rather easily turn our classification problem into a linear program, at least in the separable case. The reason why this is of interest is that linear programs have been studied quite extensively and there are even free solvers online.

The inhomogeneous case

If we want to allow a constant term, we simply add a 1 at the end of every domain point, and search for a vector $a \in R^{d + 1}$ that solves the homogeneous problem one dimension higher. This is why the difference of homogeneous vs inhomogeneous isn't a big deal.

Linear Regression

Linear regression is where we first need linear algebra and vector calculus.

Recall that, in linear regression, we have $X = R^{d}$ and $Y = R$ and a predictor $h_{a}$ for some $a \in R^{d}$ is defined by the rule $h_{a} (x) = ⟨ a, x ⟩$ . Finally, recall that the empirical squared loss function is defined as $ℓ_{S}^{(2)} (h) = \frac{1}{n} \sum_{i = 1}^{n} (h (x_{i}) - y_{i})^{2}$ . (We set $n := | S |$ .) The $\frac{1}{n}$ is not going to change where the minimum is, so we can multiply with $n$ to get rid of it; then the term we want to minimize looks like this:

$n \cdot ℓ_{S}^{(2)} (h_{a}) = \sum_{i = 1}^{n} (⟨ a, x_{i} ⟩ - y_{i})^{2}$

In order to find the minimum, we have to take the derivative with regard to the vector $a$ . For a fixed $i \in {1, . . ., n}$ , the summand is $(⟨ a, x_{i} ⟩ - y)^{2}$ . Now the derivative of a scalar with respect to a vector is defined as

$\frac{\partial y}{\partial a} := (\frac{\partial y}{\partial a_{1}} \dots \frac{\partial y}{\partial a_{d}})$

so we focus on one coordinate $j \in {1, . . ., d}$ and compute the derivative of the such a summand term with regard to $a_{j}$ . By applying the chain rule, we obtain $2 (⟨ a, x_{i} ⟩ - y_{i}) \cdot (x_{i})_{j}$ . This is just for one summand; for the entire sum we have $2 \sum_{i = 1}^{n} (⟨ a, x_{i} ⟩ - y_{i}) (x_{i})_{j}$ . So this is the $j$ -th coordinate of a vector that needs to be zero everywhere. The entire vector then looks like this:

$2 \sum_{i = 1}^{n} (⟨ a, x_{i} ⟩ - y_{i}) x_{i} .$

Now, through a process that I haven't yet been able to gain any intuition on, one can reformulate this as ${X X}^{T} a = b$ , where $X = (x_{1} \dots x_{n})$ is the matrix whose column vectors are the $x_{i}$ , and $b = \sum_{i = 1}^{n} y_{i} x_{i}$ .

Now if $X X^{T}$ is invertible the problem is easy; if not then it is still solvable, since one can prove that b is always in the range of ${X X}^{T}$ (but I'll skip the proof). It helps that $X X^{T}$ is symmetric.

Logistic Regression

Binary classification may be inelegant in sort of the same way that committing to a hypothesis class ahead of time is elegant – we restrict ourselves to a binary choice, and throw out all possibility of expressing uncertainty. The difference is that it may actually be desirable in the case of binary classification – if one just has to go with one of the labels, then we can't do any better. But quite often, knowing the degree of certainty might be useful. Moreover, even if one does just want to throw out all knowledge about the degree of certainty for the final classifier, including it might still be useful during training. A classifier that gets 10 points wrong, all of which firmly in the wrong camp, might be worse choice than a classifier which gets 11 points wrong, all of which near the boundary (because it is quite plausible that the first predictor just got "lucky" about its close calls and might actually perform worse in practice).

Thus, we would like to learn a hypothesis which, instead of outputting a label, outputs a probability that the label is 1, i.e. a hypothesis of the form h:X→Y where Y=[0,1]. For this, we need $ϕ$ to be of the form $ϕ : R \to [0, 1]$ , and it should be monotonically increasing. There are many plausible candidates; one of them is the sigmoid function $ϕ_{sigmoid}$ defined by the rule $ϕ_{sigmoid} (x) := \frac{1}{1 + e^{- x}}$ . Its plot looks like this:

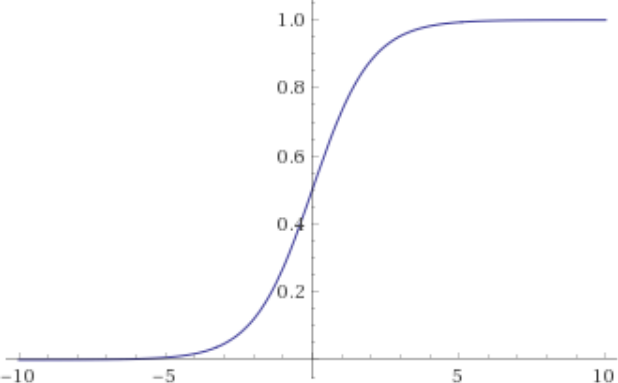
In practice, one could put a scalar in front of the $- x$ to adjust how confident our predictor will be.

How should our loss function be defined for logistic regression? In the case of y=1, we want to penalize probability mass, and in the case of $y = - 1$ , we want to penalize the missing probability mass to 1. Both is achieved by setting

$ℓ_{S}^{logistic} (h_{a}) := \sum_{j = 1}^{n} (1 + e^{- y_{j} ⟨ x_{j}, a ⟩})$

This is how it looks in the case of y=1:

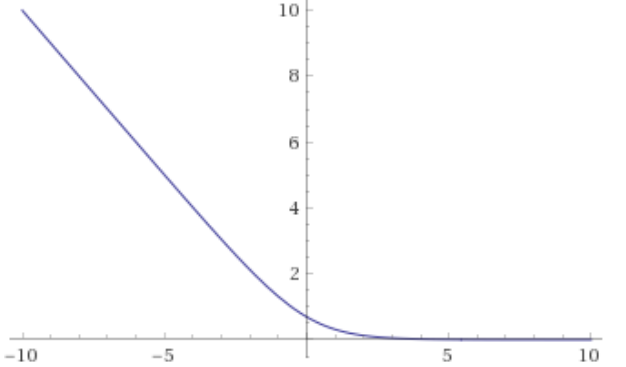
And the case of $y = - 1$ is symmetrical.

LESSWRONG
LW