TL;DR: By analyzing data from WeirdML and Aider Polyglot on score vs cost we find that the inference cost to achieve a certain score halves roughly every two monts. For example, to achieve the same score on WeirdML as gpt-4 (from June 2023), which cost about 0.6 $, we can now use llama-3.3-70b, at a cost of about 0.0014 $.

The WeirdML data

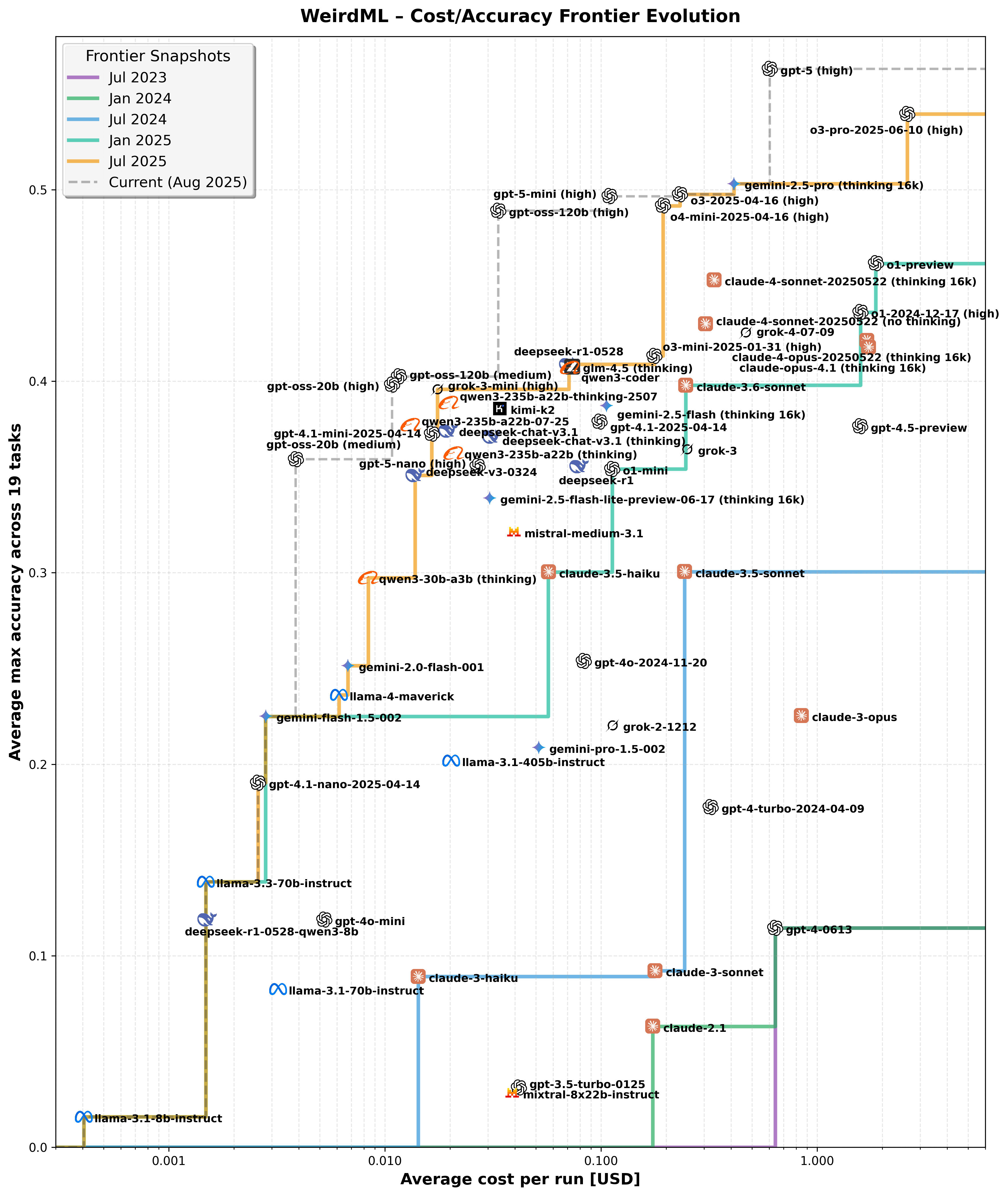
In WeirdML (homepage, data), a benchmark of 19 weird and unusual machine-learing coding tasks where models write code and iterate based on feedback. We ran all major API accessible historical models and tracked the inference cost per tasks. This lets us track how the accuracy-cost frontier moves over time.

This scatter plot shows the relationship between model release dates and their achieved accuracy. Each icon corresponds to a model positioned according to its release date on the X-axis and its overall accuracy on the Y-axis, providing an overview of how model performance has progressed chronologically. The actual datapoints are in the middle of each company logo, not the text. Also indicated are snapshots of the frontier in accuracy/cost at 6 month intervals from Jul 2023 to Aug 2025.

Another way to look at this data is to plot how the cost of achieving a certain level of performance goes down over time.

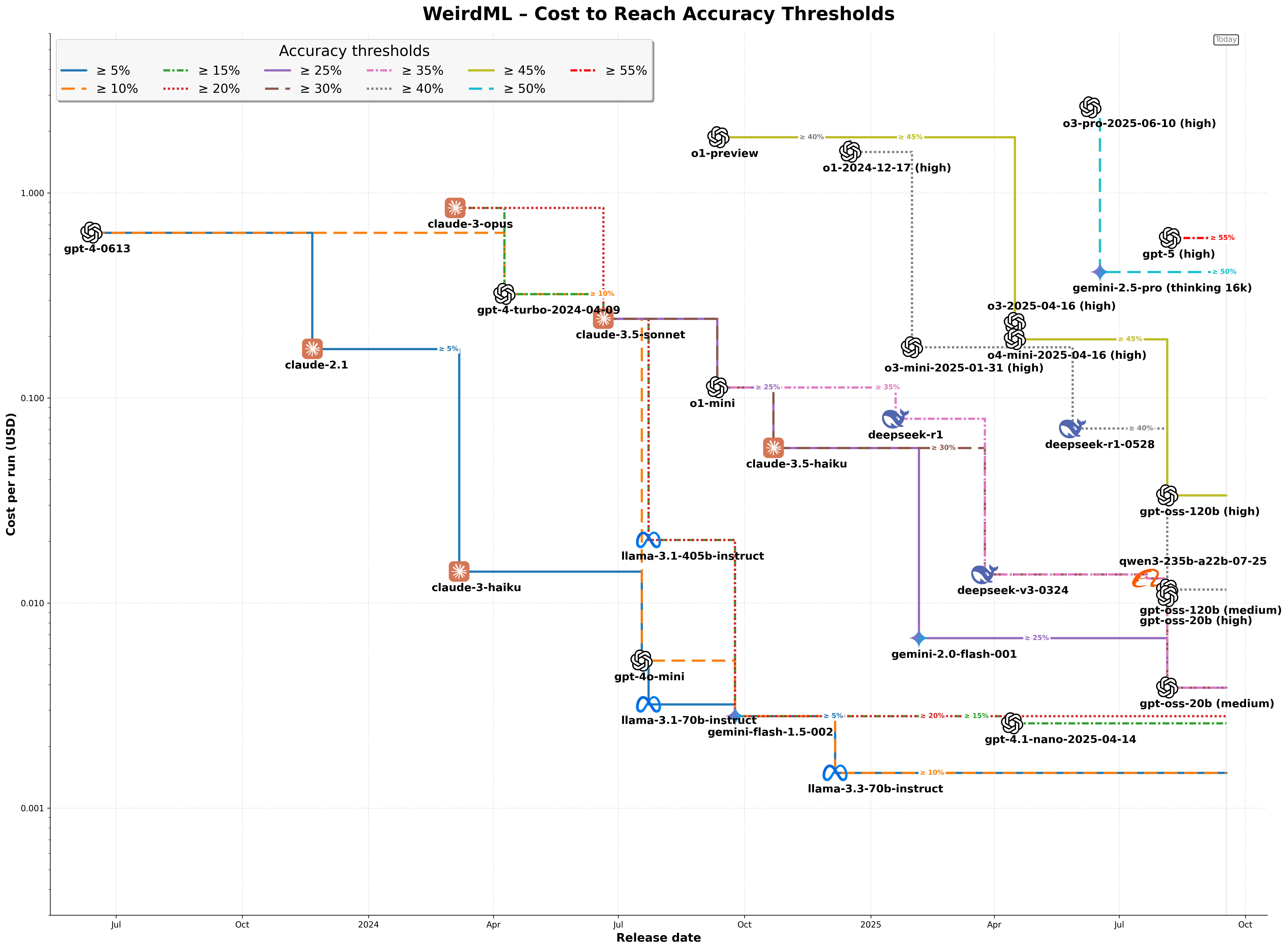
Here we see the cost to run the cheapest model that could achieve each 5% level of accuracy and how it declines over time. This is the average cost to solve a single task (in 5 iterations/model calls). We show the results for each accuracy level from 5% up to 55%, which is the highest 5% increment achieved to date.

Here we see that over these two years, the cost to achieve a given level of accuracy on WeirdML has dropped dramatically, often by >100x over two years. If we normalize the cost of every accuracy threshold to start at 1, we get the following.

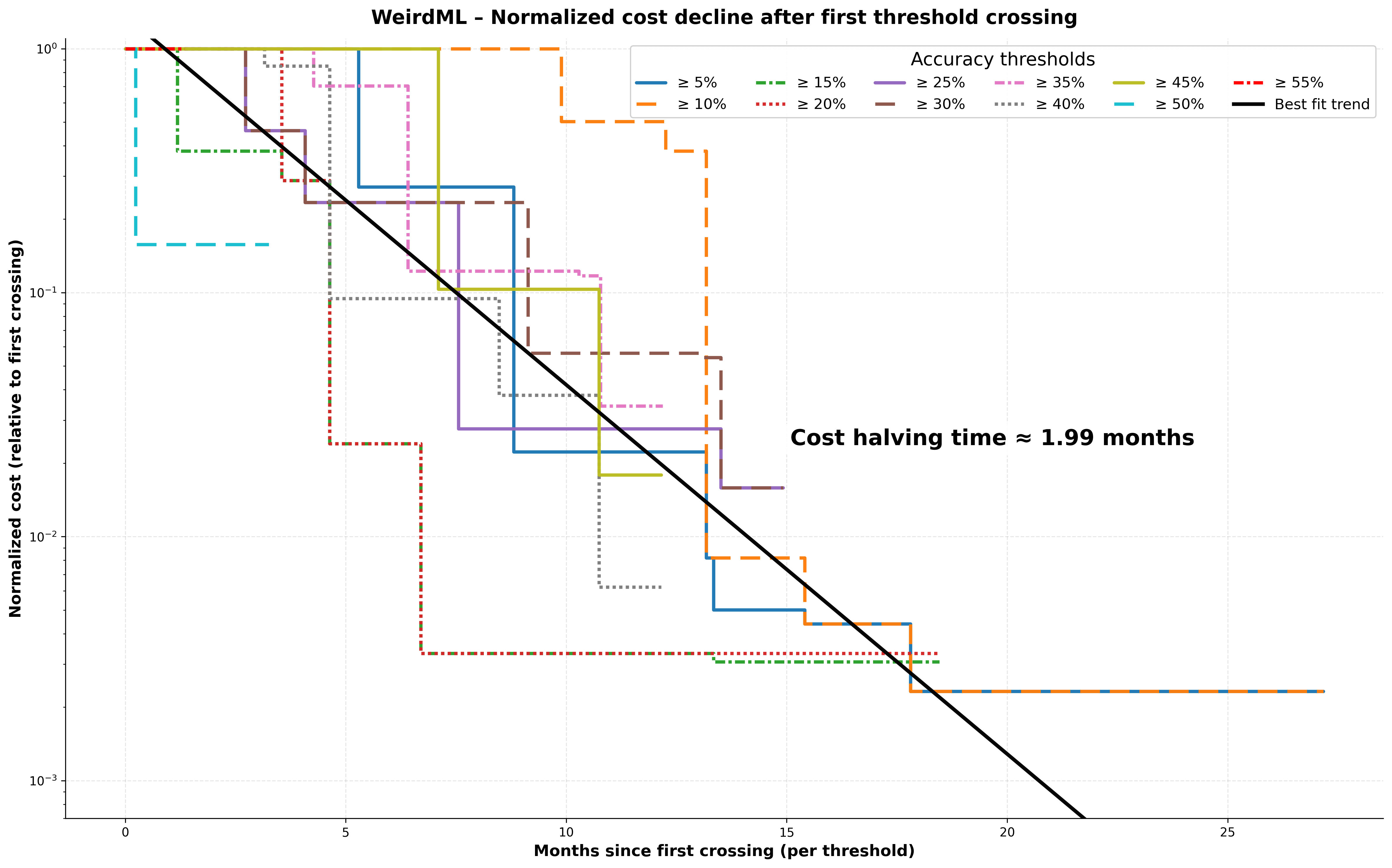
Here we see the normalized cost (the cost at each time compared to the cost when the threshold was first achieved), and how that evolves over time for each threshold. We can then fit a curve to these data.

We see that while the different curves are not on top of each other, there does seem to be a fairly clear trend.

Some caveats:

We ran all the models on WeirdML this summer (2025), but attributed those prices to the models back in time. This is typically not a problem for closed models, as the prizes for a given endpoint are usually kept the same, with price decreases typically coming from new endpoints/model versions being released. It is more of an issue with open models, which are run through one of several open model providers, which may serve the same models cheaper now than they could two years ago. However, the open models only have a big inpact on these data starting in 2025, and the models were mostly run in June 2025, so that is only half a year.
When doing this normalization, a lot can depend on the order in which models are released, e.g. if o1-preview was released a day before o1-mini, then the 35% threshold would see a huge cost decrease to start the curve, while we do not see this as they were released at the same time. In the analysis, we sample the data monthly to reduce these kinds of effects somewhat, but there are still probably a bunch of biases like this that will have some impact on the results.
The different thresholds have the same models and releases, so they are hardly independent, then again we do not estimate an error bar assuming this independence.

Fitting a curve

We want to fit a curve to the historical cost data of WeirdML. We collect data on the costs every month to weigh each time slot the same, and combine the data from all the thresold into one set of data. I'm not an expert in analyzing this sort of data, but the simplest thing we can do is to do a linear regression with

y = {log}_{2} (c o s t)

We can do the regression minimizing errors on y, i.e. ordinary least squares (OLS) or we minimize errors on x (just swap x and y in the OLS), or we can do Deming regression that minimizes errors on both assuming

σ_{x} / σ_{y} = 2

with units months/doubling.

These fits give me a halving time of 2.37 (OLS), 1.99 (Deming) and 1.67 (inverse OLS), which I think roughly brackets the range of reasonable regression choices for this data. I use the Deming estimate for the headline result.

The Aider Polyglot data

Aider Polyglot (website, data) is a benchmark testing LLMs on 225 challenging Exercism coding exercises across C++, Go, Java, JavaScript, Python, and Rust. They also track cost, and have results from historical models, althugh the results I could find did not go much farther back than a year. I wanted to repeat my analysis on this data as a sanity check on the WeirdML results.

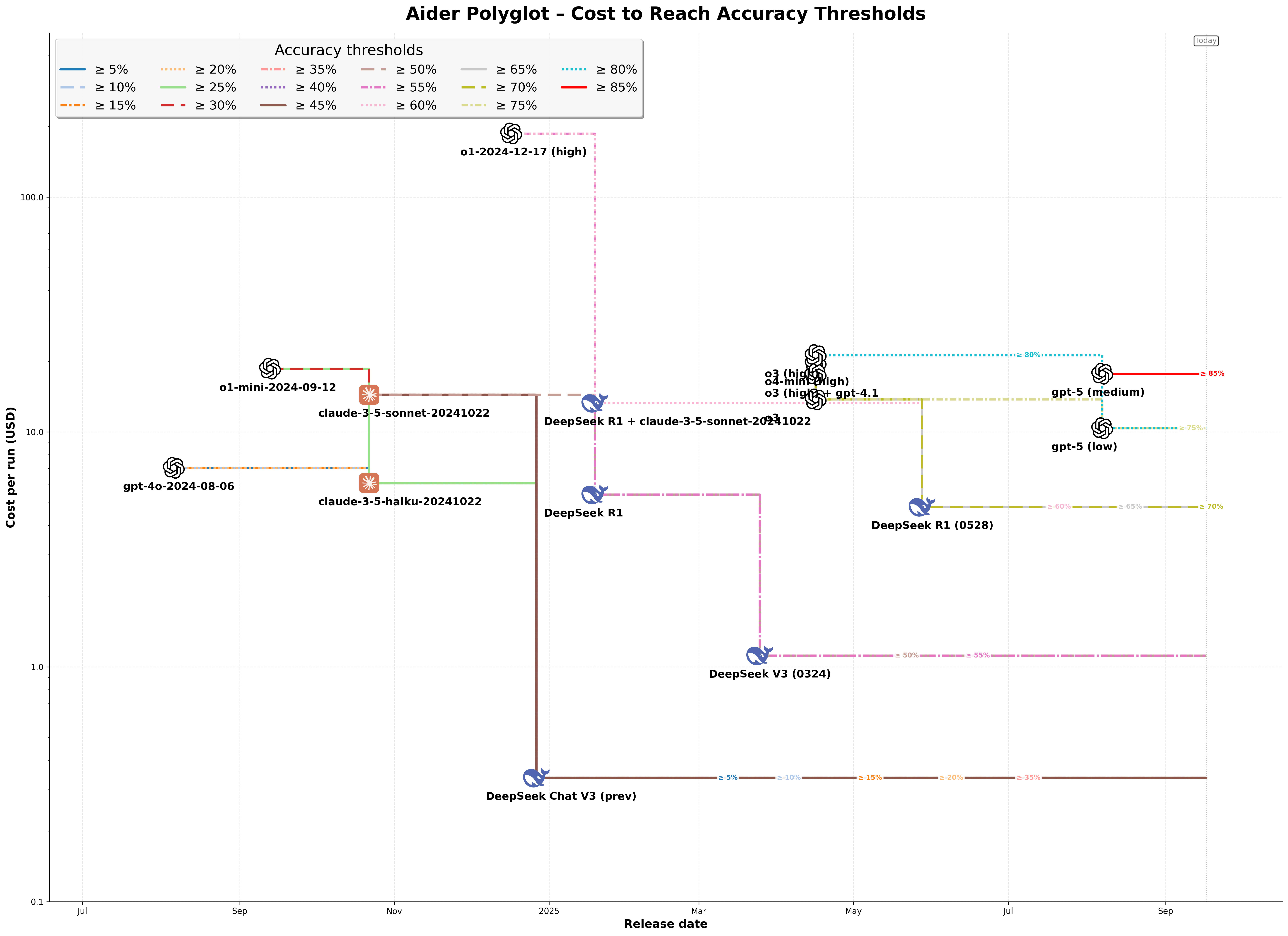
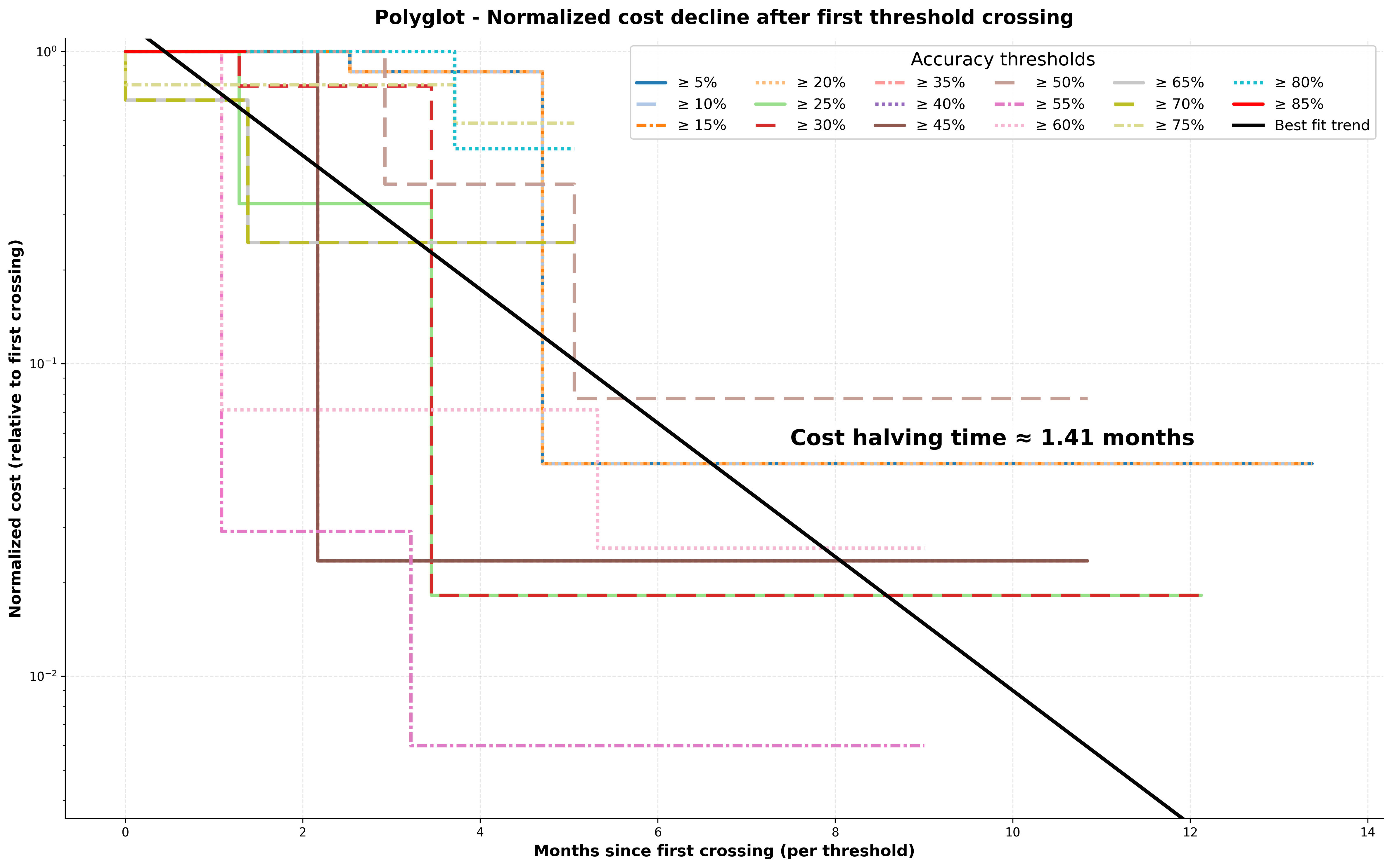
The corresponding results for Aider Polyglot are a halving time of 2.43 (OLS), 1.41 (orthogonal) and 1.03 (inverse OLS).

The Aider Polyglot data does not have as long a timeline to work with and it also does not have results from many of the small and cheap models that could probably achieve many of the lower thresholds at a cheaper price today, but it still does give results in the same ballpark as for WeirdML.

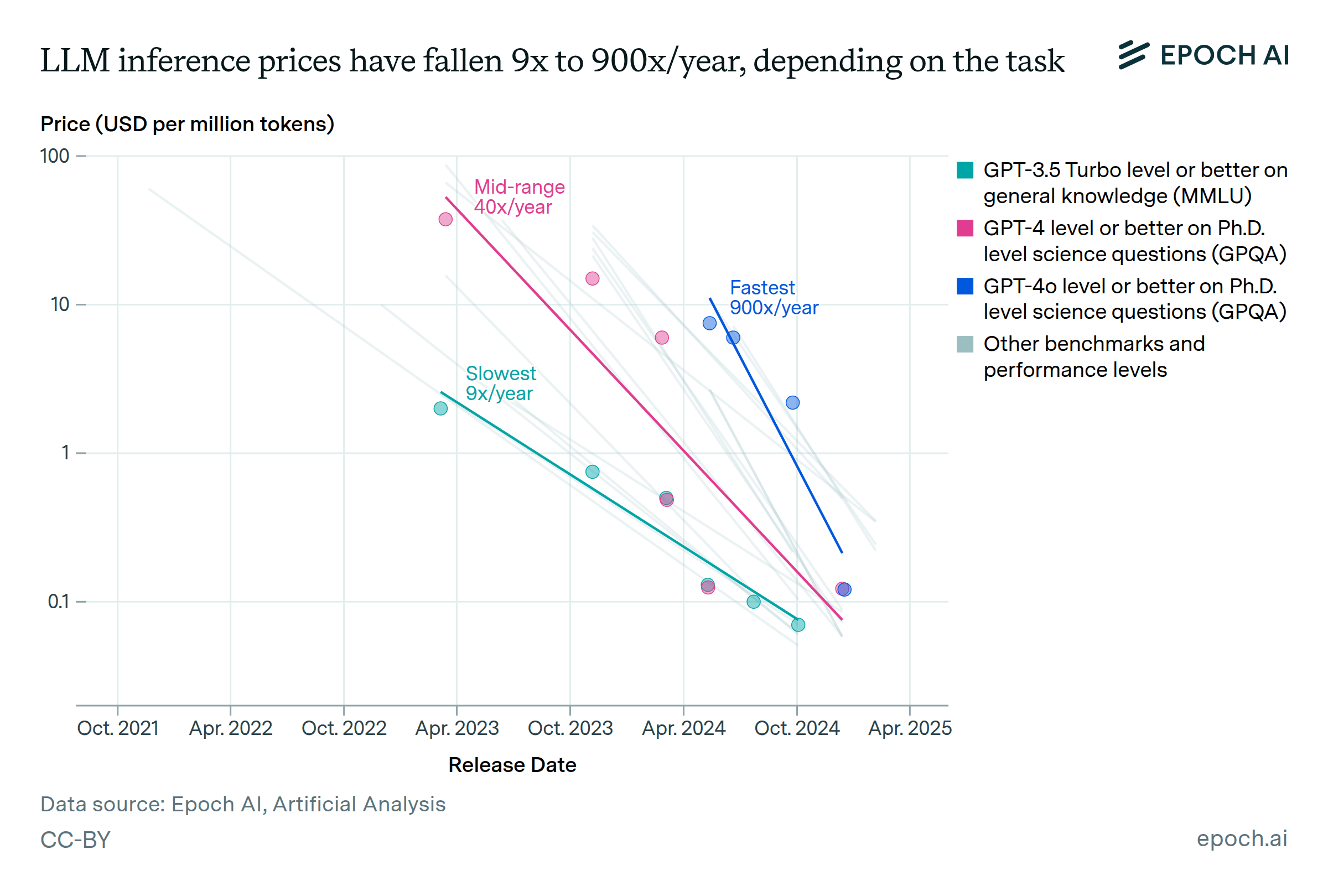
Epoch AI results

Epoch AI did a similar analysis this spring looking mostly at science and general knowledge benchmarks like GPQA and MMLU. They find that inference costs decrease by a factor of 9 - 900 in one year. This corresponds to halving times of 1.2 months to 3.8 months, so our results are well within this range.

LESSWRONG
LW