The generalized Sierpinski-Mazurkiewicz theorem.
2johnswentworth
5Donald Hobson
2johnswentworth
2Donald Hobson
New Comment
Huh, that's a really cool theorem. Someone should make a distillation of this post with cool fractal visualizations (see e.g. Chaos Games for some idea of the relation).
Sure. The image is kind of a diffuse cloud of points. Its actually dense on the plane. But I can still kind of plot it by gradually fading points out. The transforms I used are shifting right by 0.1 and rotating clockwise by 1 radian. Ie this image is K, st shift_right(K) Rotate_clockwise(K)=K
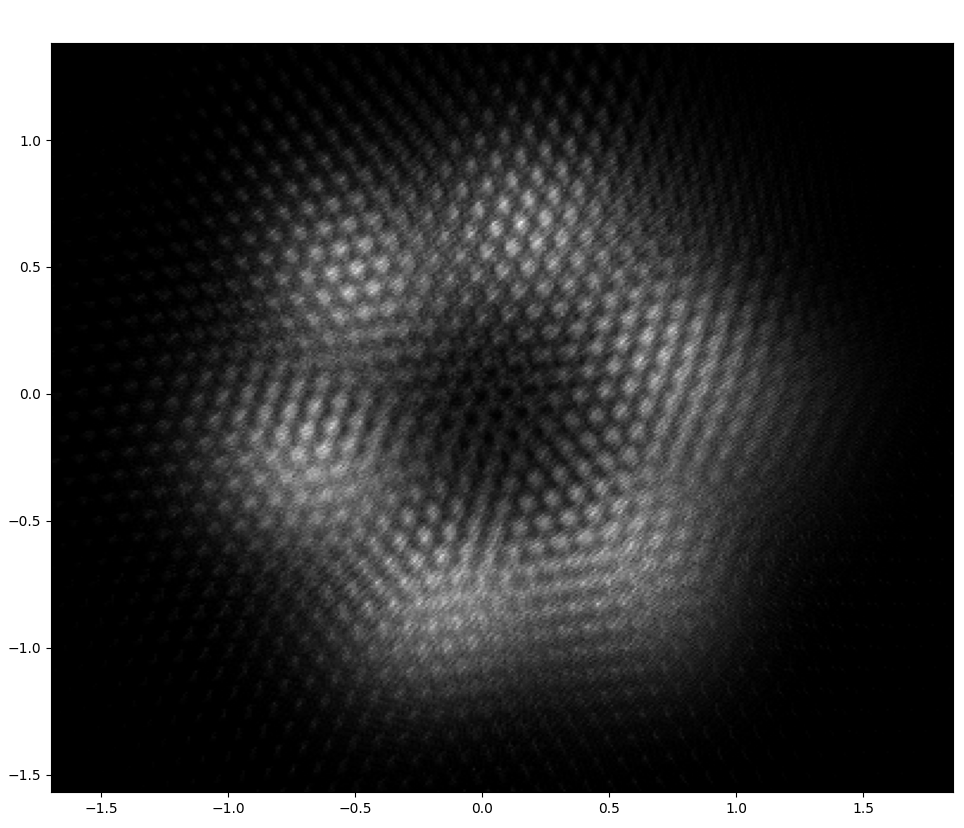
Here is a link (as lesswrong doesn't seem to support animated gifs in comments)
https://i.imgur.com/CHXYOZf.gif
Note that the points are gradually fading out, if you shift a bright point right by 0.1, you find a slightly fainter point.
Curated and popular this week
Suppose any uncountable set S and any countable set of bijective transformations T={T1,T2,...} ∀i Ti:S→S bijective.
Then assuming that for all pairs of distinct finite sequences of transformations [p1,p2,...pm] and [q1,q2...qn] that the set {s∈S:p1∘p2..pm(s)=q1∘q2..qn(s)} is countable.
Then there exists a set K⊂S,K≠∅ partitioned into K1,K2,... such that Ki=Ti(K)..
Proof.
Consider the set of all sequences of transformations (type signature N→T)
Form the equivalence relation ∼ by a∼b⟺∃m,n∈N:∀i∈N:am+i=bn+i
This is the sequences that are the same up to a finite number of insertions, deletions and replacements. Discard all the sequences equivalent to any cyclic sequence. (A sequence is cyclic if ∃m∀i:ai=ai+m. Think if these like the digits of rationals, they might do all sorts of things at first, but eventually they repeat the same thing over and over) Call the set of remaining sequences Q.
Pick a representative of each equivalence class. Call this set of representatives R.
Note that each equivalence class is countable, as for any a∼r∈R then a can be represented by (m,n,a1,a2,...am) as the rest of the sequence can be filled in using the equivalence relation ∀i:am+i=rn+i. Use countable union of countable sets a lot.
Note that, given any function f:R→S can be uniquely extended into a function f:Q→S such that f([a1,a2,...])=a1(f([a2,...]). Use the rule f(a)=a1∘a2..am∘r−1n∘r−1n−1..r−11(f(r)). This is well defined because, if we increment both m and n, then we are just applying an extra function and inverse. But those cancel each other out, by the condition in the equivalence relation. Also m−n is a fixed constant for particular a and r, because we ruled out all eventually cyclic sequences.
Pick any r∈R. For any a,b∼r, there must be only countably many s∈S such that the extension of f(r)=s has f(a)=f(b). Looking at the definition of the generalization above, we see its a finite composition of bijections. So Generalize: f(r)→f(a) is a bijection (type S→S). Let c=[am+1,am+2,...] where m,n are such that ∀i:am+i=bn+i. Then f(a)=am∘..a1(f(c)) and f(b)=bn∘..b1(f(c)). But the set of overlaps between am∘..a1 and bn∘..b1 are countable (this is where we use that strange condition) And the generalization f(c) is a bijective function of f(r).. So this rules out a countable number of s∈S.
Now there are countably many a,b∼r, so given the uncountability of S, its possible to choose s=f(r) such that ∀a,b∼r:f(a)≠f(b).
This lets us define K={f(a):a∼r}. Where Ki={f(a):a∼r,a1=Ti}={Ti(f([a2,a3,..])):a∼r}
Originally my proof tried to use transfinite induction to construct this for every r∈R, and keep them all from overlapping. Then I realized that I only needed a single r∈R, which made the proof simpler.