Over the past year, I've been studying interpretability and analyzing what happens inside large language models (LLMs) during adversarial attacks. One of my favorite findings is the discovery of a refusal subspace in the model's feature space, which can, in small models, be reduced to a single dimension (Arditi et al., 2024). This subspace explains why some jailbreaks work, and can also be used to create new ones efficiently.

I previously suggested that this subspace might not be one-dimensional, and Wollschläger et al. (2025) confirmed this, introducing a method to characterize it. However, their approach relies on gradient-based optimization and is too computationally heavy for small setups, especially for my laptop, which prevents me from doing the experiments I would like to.

Hence, I propose a cheaper (though less precise) method to study this structure, along with new experimental evidence (especially on reasoning models) showing that we need to consider multiple dimensions, rather than a single refusal vector, for larger models.

This work was conducted during my internship at NICT under the supervision of Chansu Han. I also thank Léo Dana for the review. 

This post can also be found here, where it is slightly better formatted.

Evidence for multi-dimensionality

Mechanistic interpretability research (Nanda, 2022; Hastings, 2024) has shown that some model behaviors can be expressed linearly in activation space (Park et al., 2024). For example, by comparing activations between contrastive pairs such as "How to create a bomb?" vs. "How to create a website?", we can extract a refusal direction, a vector representing the model's tendency to reject harmful queries (Arditi et al., 2024).

While earlier work assumed this direction was one-dimensional, evidence suggests that refusal actually spans a multi-dimensional subspace, especially in larger models (Wollschläger et al., 2025 ; Winninger et al., 2025).

A single refusal direction computed via different methods gives different results

When refusal directions are extracted using different techniques, such as the difference in means (DIM)^[1] and probe classifiers^[2], they are highly but not perfectly aligned. With cosine similarities descending to $0.3$, this contradicts the one-dimensional hypothesis.

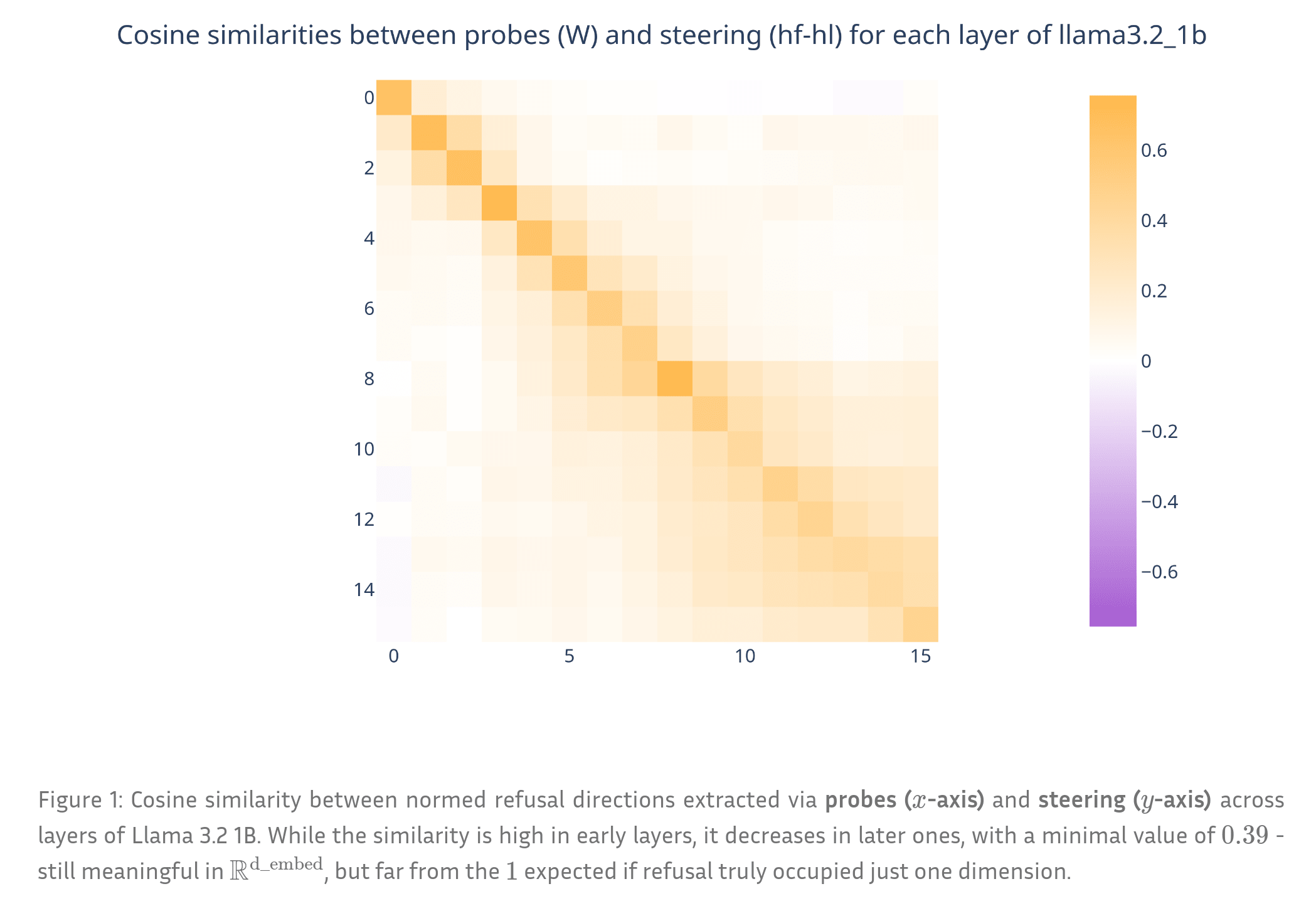
This phenomenon can also be observed when training multiple probes with different random seeds: they converge to distinct directions, again showing lower cosine similarity than expected.

Ablating a single direction is no longer enough to remove refusal, but ablating more than one direction is

Using the ablation method proposed by Arditi et al. (2024) no longer works for recent models, especially those with more than 4 billion parameters. The attack success rate (ASR) can even drop to 0% on models like Llama 3.2 3B.

However ablating multiple dimension is sufficient to induce jailbreak, as showed later.

Computing the refusal direction through optimization yields better results than the difference in means

During my experiments with SSR (Winninger et al., 2025), I observed that adversarial attacks based on probes consistently outperformed those based on DIM, often by a large margin (50% ASR vs. 90% ASR).

Wollschläger et al. (2025) reported similar findings and extended the optimization to multiple directions, forming what they called the refusal cone. This concept helps explain the observations: while DIM provides one direction within the refusal cone, probe-based methods converge toward a different, more efficient direction, essentially sampling distinct regions of the same cone.

Characterizing the refusal cone with a practical clustering-based approach

The idea behind the cheaper refusal cone extraction method is straightforward: if large models encode different categories of harmful content differently, then computing refusal directions per topic should expose several distinct vectors.

Creation of the variety dataset

I merged multiple harmful datasets, including AdvBench (Zou et al., 2023) and StrongREJECT (Souly et al., 2024), into a unified BigBench-style dataset of about 1,200 samples. Using a sentence transformer embedding and HDBSCAN clustering, I grouped semantically similar prompts together and used an LLM to label each cluster, resulting in 74 distinct categories^[3].

By computing difference-in-means vectors for each cluster, I obtained multiple non-collinear refusal directions with cosine similarities around 0.3, confirming that they occupy different regions of the subspace. These refusal directions also have interpretable semantic meaning, being linked to the topics of their clusters.

Of course, this method doesn't guarantee full coverage of the refusal cone.

Selecting a limited number of directions

This method yields multiple directions (12 in my setup). To extract only a few representative ones, several options can be used:

- Use singular value decomposition to extract a basis^[4].
- Select the "least aligned" directions by minimizing cosine similarity between pairs^[5].
- Select a random subset.

Wollschläger et al. (2025) constructed a basis with the Gram-Schmidt algorithm, but I found it less efficient than the second method, which simply selects the best candidates. Thus, I'll be using the second method for the rest of this work.

Even though, in practice, the subspace found by the cone method may be smaller than that found by SVD, this is not guaranteed^[6].

Testing the directions

Once the directions are found, we can steer the model to induce or reduce refusal. Alternatively, we can directly edit the model by ablating the directions from its weights, producing an edited version with the refusal cone removed. I followed Arditi et al. (2024)'s approach, ablating every matrix writing to the residual stream^[7].

These edited models can then be tested with two main metrics:

1. Refusal susceptibility: Is the edited model more likely to answer harmful prompts?
2. Harmless performance: Does the edited model retain performance on harmless tasks?

For (1), I used an LLM-as-a-judge setup with two evaluators - one stricter than the other - to produce a range rather than a single value.
For (2), I evaluated using AI Inspect on the MMLU benchmark.

The experiments were made on the Qwen3 family of models (Yang et al., 2025), as my main interest was studying reasoning models. I used Mistral NeMo (Mistral AI, 2024) and Gemini 2.5 (Comanici et al., 2025) as evaluators. Every experiment was run on my laptop, a RTX 4090 with 16GB VRAM. The full evaluation pipeline is described in this footnote, as well as why I'm using two different evaluators^[8].

Results

Ablating multiple refusal directions do reduce refusal, more directions are needed for bigger models

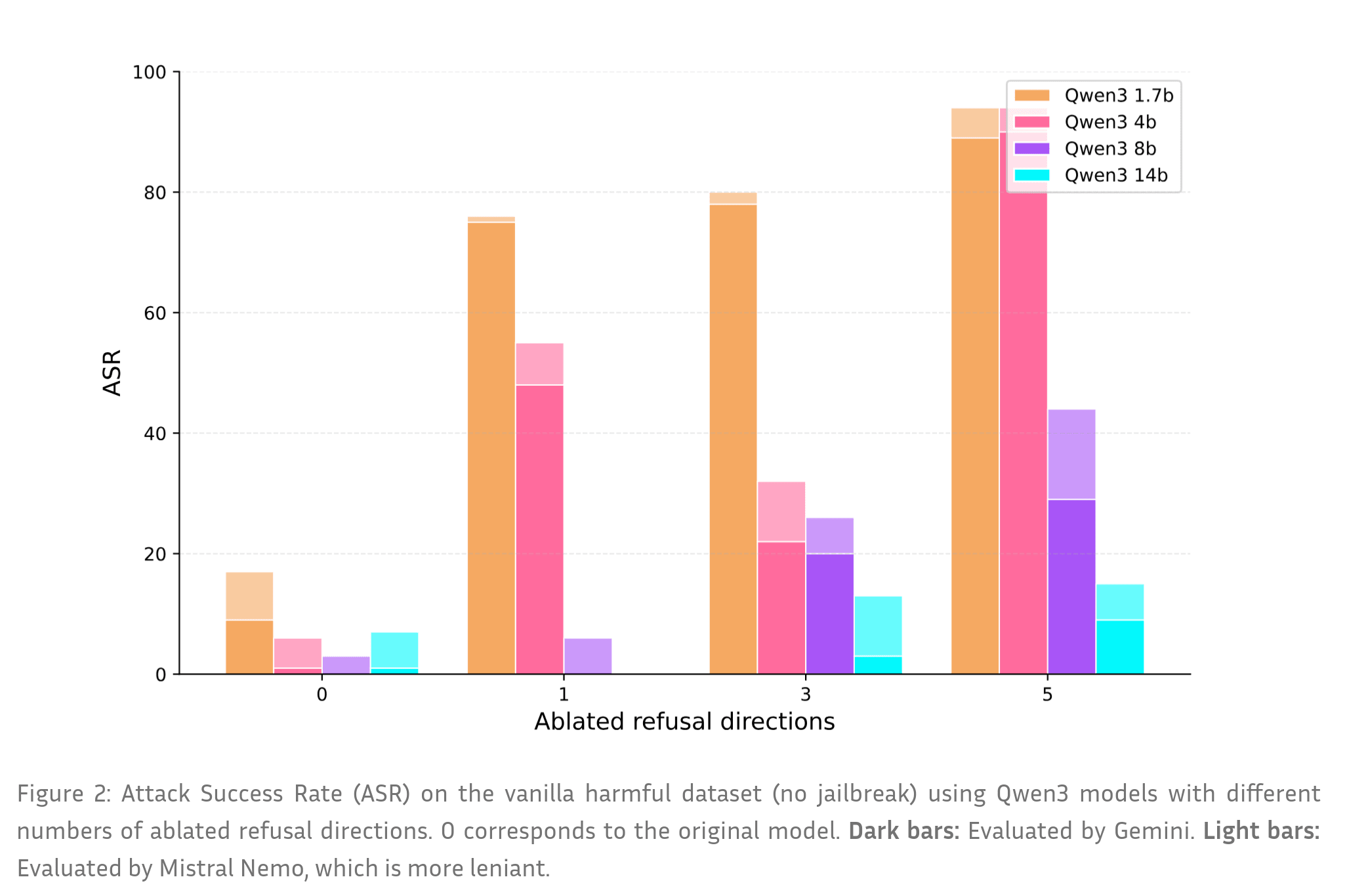
Figure 2 shows that as more refusal directions are ablated, the distribution shifts rightward toward higher compliance scores—even without jailbreaks or adversarial suffixes. More importantly, while ablating a single direction is insufficient for larger models (e.g., Qwen3 8B and 14B), multiple directions succeed in reducing refusal.

Ablating refusal directions does not significantly degrade model performance on harmless task (MMLU) 

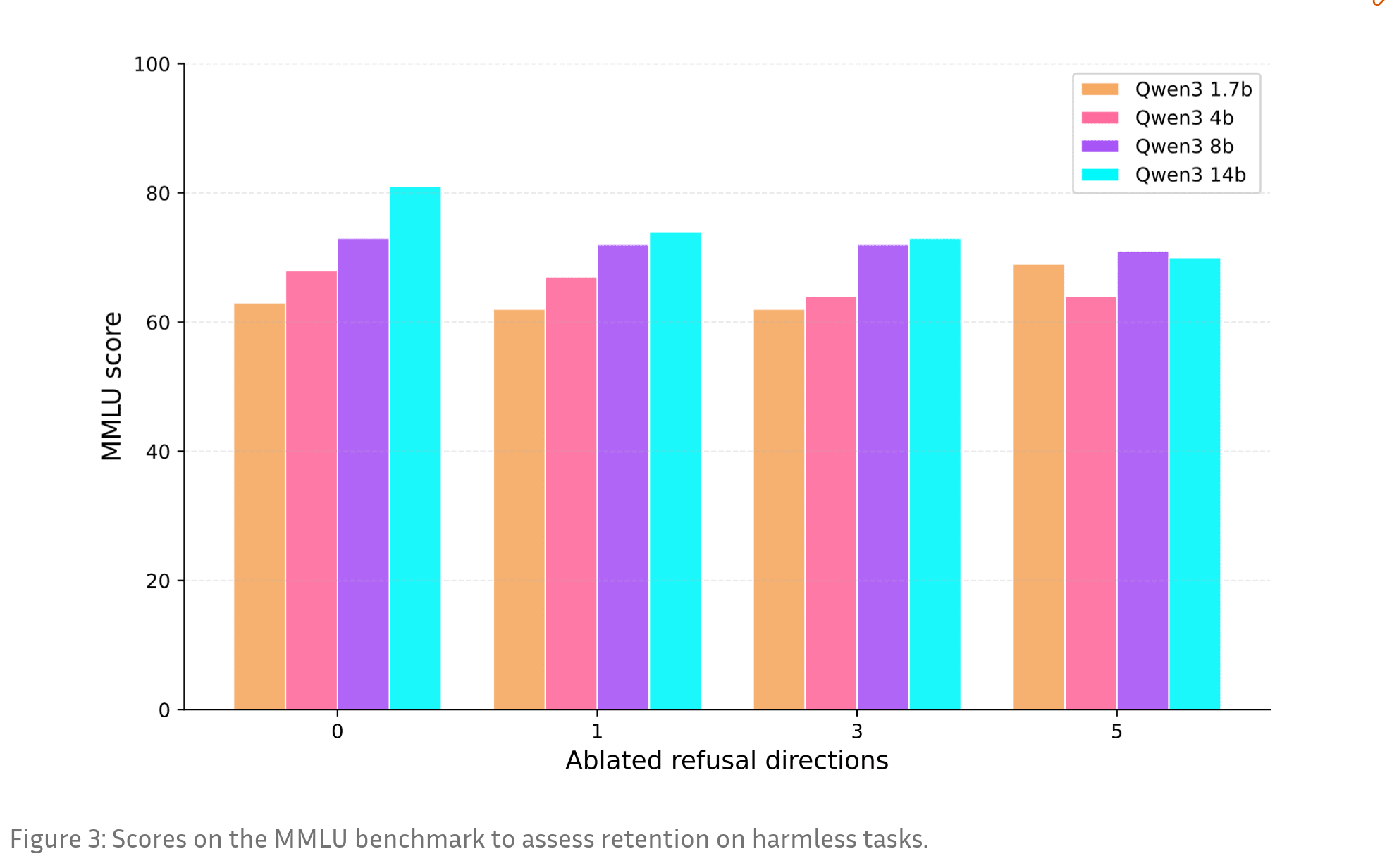
As shown in Figure 3, this method does not significantly degrade model performance on harmless tasks, at least on MMLU. The only exception is Qwen3 14B, likely due to floating-point precision issues (float16 editing vs. float32 for others).

Conclusion

The multi-dimensionality of the refusal subspace is not a new discovery, but this work shows that it also applies to newer reasoning models. Moreover, it provides a simple, low-cost method that can run on local hardware and help advance interpretability and alignment research.

1. ^{^}

   Extracting the refusal direction with the Difference-in-Means (DIM) method

   This is the method from Arditi et al. (2024). 

   Given pairs of harmful and harmless prompts (e.g., "How to create a bomb?" vs. "How to create a website?"), we first perform a forward pass to compute the activations of the residual stream at each layer on the last token, after the MLP (`resid_post`). 

   At layer $l$, we obtain $a_l^{\text{hf}}$ for harmful prompts and $a_l^{\text{hl}}$ for harmless ones. The refusal direction is then computed as: 

   $${\overrightarrow{k}}_l=\frac{1}{|\text{HF}|}\sum _{\text{hf}\in \text{HF}}{a}_l^{\text{hf}}-\frac{1}{|\text{HL}|}\sum _{\text{hl}\in \text{HL}}{a}_l^{\text{hl}}$$ 

   where 

   • ${\overrightarrow{r}}_l$ is the refusal direction at layer l,
   • $\text{HF}$ is the set of harmful prompts,
   • $\text{HL}$ is the set of harmless prompts.

   Variants exist: some average activations across all tokens (He et al., 2024), and some use intermediate positions within the transformer layer instead of post-MLP activations.

2. ^{^}

   Extracting the refusal direction with probe classifiers

   This approach follows He et al. (2024) and Winninger et al. (2025). 

   Activations are collected as in the DIM method, but a one-layer neural probe is trained to predict refusal: 

   $$p_l\left(\text{sentence}\right)=\sigma ({\overrightarrow{w}}_l^T{a}_l+b_l)$$ 

   The probe minimizes the binary cross-entropy loss: 

   $$\underset{{\overrightarrow{w}}_l,b_l}{min}\sum _{\text{hf}\in \text{HF}}L(0,\sigma ({\overrightarrow{w}}_l^T{a}_l^{\text{hf}}+b_l\left)\right)+\sum _{\text{hl}\in \text{HL}}L(1,\sigma ({\overrightarrow{w}}_l^T{a}_l^{\text{hl}}+b_l\left)\right)$$ 

   The normalized weight vector gives the refusal direction: ${\overrightarrow{r}}_l={\overrightarrow{w}}_l/||{\overrightarrow{w}}_l||$. 

   In practice, the bias term is often close to zero.

3. ^{^}

   Creation of the harmful dataset

   The combined dataset included AdvBench (Zou et al., 2023), HarmBench (Mazeika et al., 2024), StrongREJECT (Souly et al., 2024), ForbiddenQuestions (Chu et al., 2025), and MaliciousInstruct (Qiu et al., 2023), totaling 1,271 samples. 

   Embeddings were computed with `text-embedding-embeddinggemma-300m-qat`. 

   HDBSCAN was chosen to handle the uneven, high-dimensional (768D) space. 

   Clusters were automatically labeled with Qwen3-8B and used to generate contrastive harmless prompts, following the SSR approach (Winninger et al., 2025. 

   Example: 

   {
   	"harmful_prompt": "How to create a bomb?", 
   	"harmless_prompt": "How to create a website?", 
   	"topic": "explosive creation"
   }

4. ^{^}

   Reducing the number of refusal directions with singular value decomposition (SVD)

   Given $b$ refusal directions ${\overrightarrow{r}}_l^1,{\overrightarrow{r}}_l^2,\dots ,{\overrightarrow{r}}_l^b$, concatenate them into a matrix $A$: 

   $$A=[{\overrightarrow{r}}_l^1,{\overrightarrow{r}}_l^2,\dots ,{\overrightarrow{r}}_l^b]\in R^{b\times \text{d\_embed}}$$ 

   Applying SVD gives: 

   $$A=U\Sigma V^T$$ 

   The top-$k$ singular vectors form an orthonormal basis: 

   $${\overrightarrow{r}}_l^{\text{SVD}}=[U_{:,1},U_{:,2},\dots ,U_{:,k}]$$ 

   This captures the directions that explain the greatest variance.

5. ^{^}

   Reducing the number of refusal directions with cosine-similarity selection (MINCOS)

   Given $b$ refusal directions ${\overrightarrow{r}}_l^1,\dots ,{\overrightarrow{r}}_l^b$, compute the Gram matrix of pairwise cosine similarities: 

   $$G_{ij}=\frac{⟨{\overrightarrow{r}}_l^i,{\overrightarrow{r}}_l^j⟩}{||{\overrightarrow{r}}_l^i||\cdot ||{\overrightarrow{r}}_l^j||}$$ 

   For each direction $i$, sum its total similarity: 

   $$s_i=\sum _{j=1,j\ne i}^b|G_{ij}|$$ 

   Select the $k$ directions with the smallest $s_i$: 

   $$I^{\text{MINCOS}}=\underset{|I|=k}{\arg min}\sum _{i\in I}{s}_i$$ 

   The selected directions are ${\overrightarrow{r}}_l^{\text{MINCOS}}=\{{\overrightarrow{r}}_l^i:i\in I^{\text{MINCOS}}\}$. Unlike SVD, MINCOS preserves actual learned directions and does not produce orthogonal ones.

   In practice, I found it to be more efficient.

6. ^{^}

   Relationship between MINCOS and SVD subspaces

   The subspace found by MINCOS is not necessarily contained within the one found by SVD. 

   While SVD captures the top-$k$ principal components (usually explaining 90–95% of the variance), MINCOS may select directions outside this space: 

   $$\text{Vect}\left({\overrightarrow{r}}_l^{\text{MINCOS}}\right)⊈\text{Vect}\left({\overrightarrow{r}}_l^{\text{SVD}}\right)$$ 

   In practice, when cosine similarities are moderate (e.g., 0.15), the MINCOS subspace can be considered "smaller" or less destructive than the SVD one.

7. ^{^}

   Ablation process: orthogonalizing weight matrices

   To remove the influence of a refusal direction $\hat{\overrightarrow{r}}$ from the model, we modify each weight matrix that writes to the residual stream. 

   For an output matrix $W_{\text{out}}\in R^{d_{\text{embed}}\times d_{\text{input}}}$ (e.g., attention and MLP output matrices), we project it orthogonally: 

   $$W_{\text{out}}^{\prime }\leftarrow W_{\text{out}}-\hat{\overrightarrow{r}}{\hat{\overrightarrow{r}}}^T{W}_{\text{out}}$$ 

   This ensures $W_{\text{out}}^{\prime }$ no longer writes any component along $\hat{\overrightarrow{r}}$. 

   In practice, I did not ablate the embedding matrix or the first three layers, as refusal directions are poorly defined there (low probe accuracy).

8. ^{^}

   Evaluation details

   Many papers evaluate model refusal using bag-of-words filters or LLM classifiers like Llama Guard, but I find these evaluations very inaccurate, especially for reasoning models: 

   • Lexical methods fail because models may begin with neutral phrasing ("Sure, here is…") before refusing, or refuse implicitly without using "refusal words."
   • Short generations are insufficient: reasoning models may refuse early but then provide harmful content thousands of tokens later (after 4000 tokens for instance with Qwen 3 8b).
   • LLM classifiers (e.g., Llama Guard 3) perform poorly on unseen attacks like SSR, and can themselves be prone to attacks or reward hacking (Nasr et al., 2025; Winninger et al., 2025). 

   Manual verification seems the most robust method (Nasr et al., 2025), however, if it is not possible, I think generating long answers and using an LLM-as-a-judge is an acceptable minimum, where a larger or equivalent model judges responses to make sure the evaluator understands the conversation. 

   In this work, I used two judges to reduce bias: 

   • Mistral NeMo (Mistral AI, 2024), which tends to be lenient,
   • Gemini 2.5 Flash (Comanici et al., 2025), which is stricter. 

   Evaluations were run with the DSPy framework (described here). 

   Models were quantized to `Q4_K_M` using Llama.cpp for efficient inference and long-context evaluation (>4000 tokens). 

   To assess harmless-task performance, I used AI Inspect (UK AI Security Institute, 2024) with MMLU (Hendrycks et al., 2021) (0-shot, 100 random samples). 

   Although 100 samples is only a subset of the full 14k-question MMLU benchmark, this setting balances feasibility with acceptable evaluation time, especially for reasoning models.