In a recent episode of Rationally Speaking, Julia Galef and Matt Yglesias discuss why they incorrectly supported the Iraq war back in 2003. At some point, (I think - I can’t seem to find it in the transcript) Julia mentions that in the absence of good evidence, ad hominem attacks can be legitimate evidence against someone’s claim.

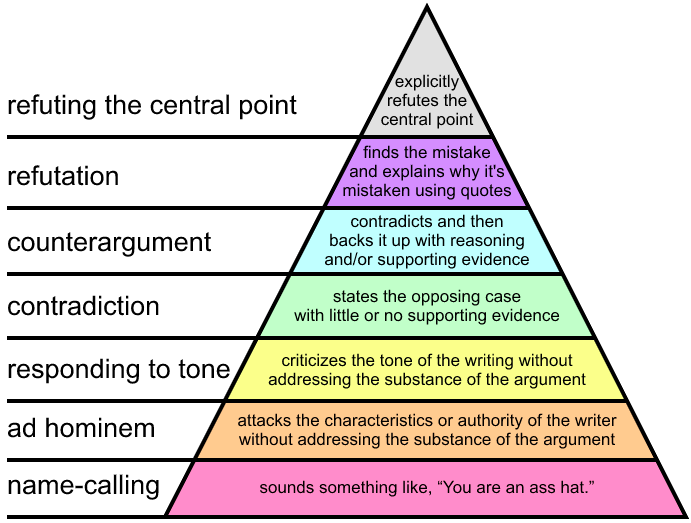
I think the idea is pretty simple: if someone is known to be a liar, or just frequently does things you find to be wrong or immoral, it’s more likely that anything he or she says is incorrect. For example:

Alice: We have to invade Iraq to prevent Saddam from getting WMDs

Bob: But Bush sucks!

Is really just a less elegant way of saying:

Alice: We have to invade Iraq to prevent Saddam from getting WMDs

Bob: Much of the evidence coming from our national security establishment in favor of war has been gathered or communicated by the Bush administration, which I believe to be generally dishonest and to have an immoral and incorrect understanding of foreign policy. While I do not know enough about the situation in Iraq to make an object-level objection to the specific points they are making, these general facts reduce the probability both that their factual claims regarding the existence of WMDs are true and that the expected results of an invasion are positive.

This seemed pretty clever and interesting, so I thought it would be fun to do the same for a few other (ostensible) logical fallacies (list here). The quotes under each heading come from the Wikipedia page linked.

Fallacy Fallacy

Argument from fallacy is the formal fallacy of analyzing an argument and inferring that, since it contains a fallacy, its conclusion must be false.

Steelman

Ok, obviously it is not strictly true that

argument contains a fallacy —> conclusion incorrect

Nonetheless, an argument containing a fallacy probably is evidence against the conclusion being correct.

As Jonathan Haidt writes in The Righteous Mind, explicit reasoning is a mechanism of post-hoc justification, designed to persuade others of our intuitions. If people generally try to make sound, coherent arguments no matter the real reason for one’s conclusion, then failure to come up with a sound argument probably indicates that no coherent argument for the conclusion in question exists, in which case the conclusion’s validity is unlikely.

Conjunction (or Linda) Fallacy

The conjunction fallacy (also known as the Linda problem…) is a formal fallacy that occurs when it is assumed that specific conditions are more probable than a single general one.

And the canonical example:

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

Which is more probable?

Linda is a bank teller.

Linda is a bank teller and is active in the feminist movement.

The answer (we are told) is (1). A single statement, A, must be at least as likely as that statement and another, A and B.

Steelman

Suppose instead we compare two separate worlds in which each statement is provided instead of one world in which they are presented side-by side. Also, let’s now assume that a real acquaintance is telling us the information, instead of God or some social scientist on a survey. So, it would look something like this:

In world A, you are told by your friend John that Linda is 31 years old, single, outspoken, and very bright bank teller. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. What is the probability that Linda is a bank teller?

In world B, you are told by your friend John that Linda is 31 years old, single, outspoken, and very bright bank teller active in the feminist movement. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. What is the probability that Linda is a bank teller and a feminist?

In real life, people don’t pull out propositions like “Linda is a bank teller” from nowhere. Depending on what you know about your friend John, it seems plausible that his very inclusion of the congruent “feminist” detail in the second scenario actually increases the likelihood of the incongruent “bank teller detail” being correct enough to offset the probabilistic decrease caused by the feminist detail itself.

For example, all the information given in world A might have been read off of a resume (with the activism information inferred from college club involvement), in which case we might think that there is a 20% likelihood that the resume is out-of-date and Linda is no longer a bank teller.

If John knows about Linda’s current political activism, however, we might instead assume that he and Linda are close acquaintances. If so, the chance of his information being out-of-date declines significantly, and perhaps we now assume only a 10% chance that any of the information is wrong.

Begging the question

To "beg the question"…is to attempt to support a claim with a premise that itself restates or presupposes the claim. It is an attempt to prove a proposition while simultaneously taking the proposition for granted.

Steelman

First example, from Wikipedia:

"Opium induces sleep because it has a soporific quality.”

Alright, this isn’t very creative but I’ll say it anyway. A claim or argument that begs the question/assumes its conclusion can be completely, 100% sound. It might not be a very good or useful explanation or argument, but there’s nothing improper going on.

The first example above is useless as an explanation that might help a psychopharmacologist design a novel sedative, but there’s no actual fallacy going on. Lucky for me, I still have the first-order logic calculator/checker/creator program that I had to download for a logic class a while back. We can translate the argument as either of the following:

As you can see, according to Fitch at least, both forms are entirely sound. In other words, the premise(s) logically imply the conclusion. The sense that something deceptive is going on, I think, comes from the fact that the arguments are much simpler than they seem at first glance. For instance, statements of the form “X does A because B” usually imply that B and A are not mere synonyms.

And a second example:

“Opium induces sleep because it contains Morphine-6-glucuronide, which inhibits the brain's receptors for pain, causing a pleasurable sensation that eventually induces sleep."

I legitimately don’t see anything wrong here. What does Wikipedia have to say?

[It takes] the form of an unstated premise which is essential but not identical to the conclusion, or is "controversial or questionable for the same reasons that typically might lead someone to question the conclusion"

I think this is saying that the clause “pleasurable sensation that eventually induces sleep” is just as questionable as the desired conclusion, “opium induces sleep"?

Well, maybe, but I disagree. When describing the causal chain of any physical process, there’s going to be a black box somewhere. It might be large enough to encompass the entire explanation, as with “morphine induces sleep because it is soporific,” or as small as physics having no explanation for the most fundamental particle interactions.

For instance, we might expand the above explanation to include fifteen more steps between “pleasurable sensation” and “inducing sleep,” ending with “and then the adenosine receptors fully activate, leading to sleep.” Does the entire explanation/argument uselessly “beg the question” just because we can’t fully explicate the causal chain between these two final steps? I don’t think so. We know a lot more about the psychopharmacology of morphine than we did before!

No True Scotsman

Probably best illustrated with an example:

Person A: "No Scotsman puts sugar on his porridge."
Person B: "But my uncle Angus is a Scotsman and he puts sugar on his porridge."
Person A: "But no true Scotsman puts sugar on his porridge.

The No true Scotsman is committed when the arguer satisfies the following conditions:

not publicly retreating from the initial, falsified assertion

offering a modified assertion that definitionally excludes a targeted unwanted counterexample

using rhetoric to hide the modification

Steelman

I have two thoughts on this one. First, we might be able to rephrase the example like this:

Person A: "No Scotsman puts sugar on his porridge."
Person B: "But my uncle Angus is a Scotsman and he puts sugar on his porridge."
Person A: “Therefore, your uncle is not a Scotsman as I define the term.”

Second, and more substantively, is that this fallacy depends far too heavily on “Scotsman” or whatever being a natural category with an unambiguous definition. As Ludwig Wittgenstein argued, a word or concept’s meaning is more like a “family resemblance” - a cluster of correlated features that generally but do not always go together.

A central example of some category might share virtually all such features in an unambiguous form, but there is no definitive way of classifying something as a member or non-member of some category. Philosophers and linguists can debate this all they want, but the point is clear to anyone who intuitively understands the futility of determining whether a hotdog is “really” a sandwich.

Back to the point: the concept of “Scotsman” might be better understood as referring to a cluster of correlated features, such as being born in Scotland, having a Scottish accent, and not putting sugar in one’s porridge. Some people are clearly Scotsmen, but what about someone who was born in Scotland but moved to Norway when he was an infant? What about someone who only puts sugar in his porridge on Tuesdays?

Person A is probably using “true Scotsman” to mean a central, unambiguous member of this group. So, there might really be a substantive disagreement between person A and person B as to the importance of the feature “doesn’t put sugar in his porridge” as one of several correlated features underneath the “Scotsman” umbrella. No fallacy to be found.

Correlation does not imply causation

Or, if you want to sound smart, cum hoc ergo propter hoc.

No explanation needed for this one. While literally true at face value, I think the phrase is overused:

Steelman

Others have made a similar point before, but I can’t recall where so please forgive me for intellectual plagiarism.

While I wouldn’t go as far as to say that genuinely spurious correlations never exist, I think there is quite often some causal relationship between two correlated variables, X and Y. Of course, this need not be that X causes (—>) Y or that Y —> X. Maybe X—>A—>B—>C—>Y, or Z—>A—>B—>X and separately Z—>C—>Y.

That’s a lot of letters, so here are some examples. Over the last hundred years, typewriter production has fallen while global CO2 emissions have risen. Obviously, there is no direct causal link between these two trends.

However, I don’t think it would be fair to call this entirely spurious either. Both can be attributed, in some fashion, to the rise of the industrial economy. Describing the precise causal pathways involved is above my pay grade, but there is a genuine connection here.

Maybe that was too easy. Let’s head over to this website with thousands of “spurious correlations” for something harder:

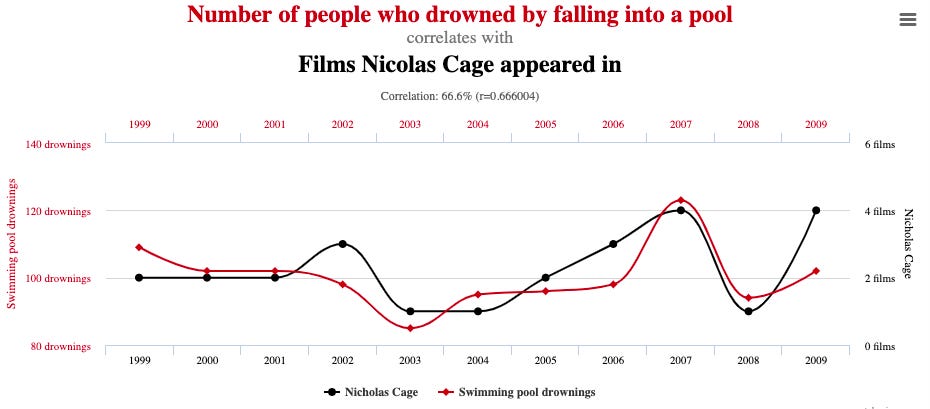
I don’t know anything about pool drownings or Nicholas Cage, so I can’t tell a good story about this one. Likewise, it’s easy to invent post-hoc explanations of any relationship. However, it seems possible that even pool drownings and Nicholas Cage appearances aren’t entirely unrelated.

For example, might the dip in 2008 for both be caused (somehow) by the Great Recession? Perhaps people go swimming less when times are bad, and movie studios slow down production. I have no idea, but we shouldn’t be too quick to assume that there are no causal gears turning underneath the surface.

Conclusion

I think one commonality between the five fallacies I’ve considered is that all commit a form of the motte and bailey fallacy (which would be worth trying to steelman in its own right!), like this:

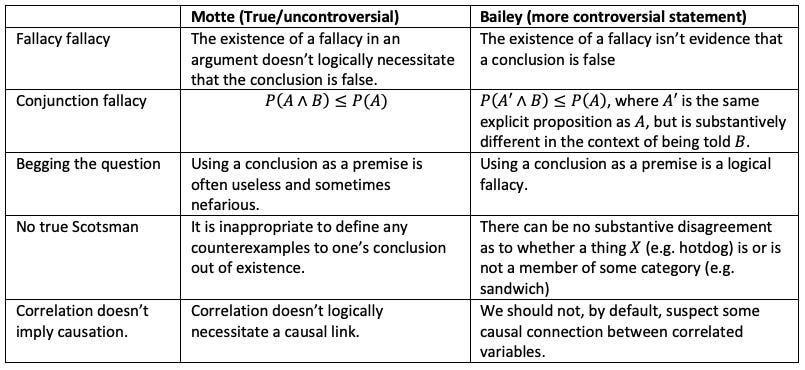
There are about a thousand other types of fallacy on the Wikipedia list, but I think I’ll stop here for now. Maybe round two in another post!