I think I must be missing something. As the number of traders increases, each trader can be less risk averse as their personal wealth is now a much smaller fraction of the whole, and this changes their strategy. In what way are these individuals now not EU-maximizing?
That example with traders was to show that in the limit these non EU-maximizers actually become EU-maximizers, now with linear utility instead of logaritmic. And in other sections I tried to demonstrate that they are not EU-maximizers for a finite number of agents.
First, in the expression for their utility based on the outcome distribution, you integrate something of the form, a quadratic form, instead of as you do to compute expected utility. By itself it doesn't prove that there is no utility function, because there might be some easy cases like , and I didn't rigorously proof that this utility function can't be split, though it feels very unlikely to me that something can be done with such non-linearity.
Second, in the example about Independence axiom we have , which should have been equal if was equivalent to expectation of some utility function.
Introduction
Why Subagents? and Why Not Subagents? explore whether a group of expected utility maximizers is itself a utility maximizer. Here I want to discuss the converse: if a group wants to maximize some utility function as a whole, what can be said about the individual agents? Of course, if they could make decisions together, they will just compute what each agent needs to do, but what if the only thing they have is a common algorithm that each of them uses independently?
It seems that such agents, in general, don't make decisions by multiplying utilons with probabilities and instead they need to consider the whole distribution of outcomes to evaluate a choice. A similar idea was already presented in Against Expected Utility, though without the focus on the number of agents.
Specific example
Imagine two traders, who select trades independently, but pool their returns together and optimize for the expected logarithm of their total wealth (as in Kelly betting). Also I will assume for simplicity that they select the same trade for both of them, though the outcomes are still sampled independently.
So if a trade multiplies the wealth by (a random variable) X, utility for one trader would be E[logX]. But for the described group of two traders it becomes E[log(X1+X22)], where X1,X2 are independent random variables with the same distribution as X. It is not linear in terms of the outcome probabilities anymore:
U(p)=∫x1,x2(logx1+x22)p(x1)p(x2)dx1dx2Increasing number of agents
Qualitatively, as the number of agents in the group increases, the agents can afford more risky actions, thanks to the aggregation of returns. So their decision will be somewhere between what an individual agent would do to maximize E[logX] and what it would do to maximize E[X]. Even more specific example to support this intution: there is a fair coin, and the agent can bet fraction f of the wealth available to them on a certain side, which will turn into 3f if the coin lands this side and 0 otherwise, i.e. their wealth will be multiplied by either 1+2f or 1−f.
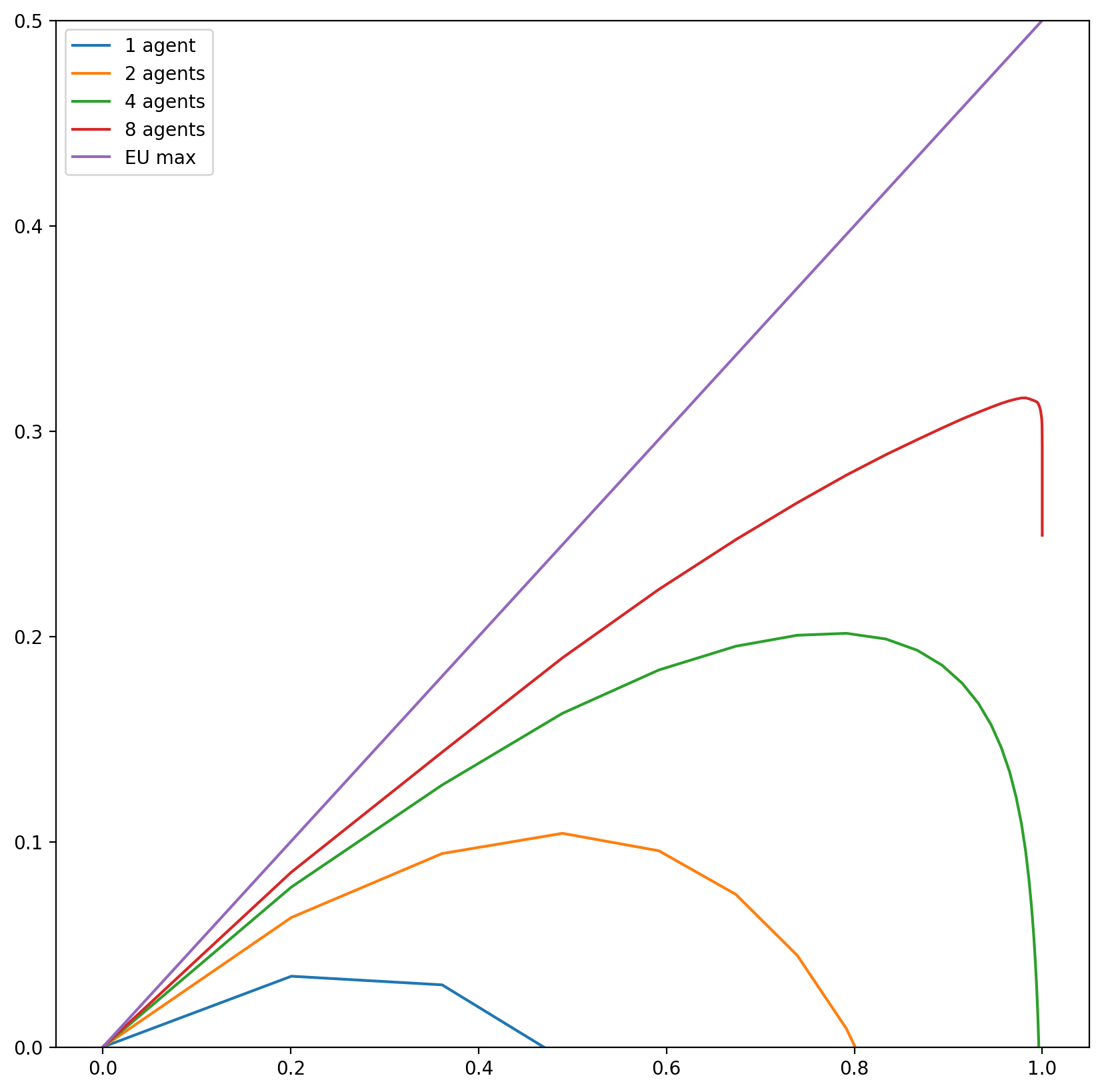
So as the number of agents increases, each agent becomes closer to maximizing E[X], but for any finite case there is still some risk-aversion. In particular, any distribution of outcomes that allows the wealth to become zero is still infinitely bad, because if it happens to all agents at the same time, their total wealth will become zero.
Violation of Independence axiom
As the VNM theorem says that under some assumptions agents can be seen as maximizing expected utility, a natural question is which assumptions don't hold in this case?
I have an example demonstrating that Independence doesn't apply to the agents described above. There will be two lotteries: A which simply preserves the money, and B which multiples them either by 10−100 or by 1020 with equal probability. Also consider A′=0.5A+0.5A=A and B′=0.5A+0.5B (i.e.A or B with equal probability).
What are the "utilities" here?
U(A)=U(A′)=log1=0U(B)=14[log10−100+2log10−100+10202+log1020]≈14[log10−100+2log10202+log1020]≈−23.4U(B′)=116log10−100+216log10−100+10202+116log1020+2[18log1+10−1002+18log1+10202]+14log1≈5.32Or if you don't trust algebraic manipulations, here is a Python simulation.
Anyway, we see that A≻B, but 0.5A+0.5A≺0.5A+0.5B, i.e. a possibility of another outcome reverses the preference.
Conclusion
I don't know what is the optimal solution to this problem and perhaps it doesn't have a simple form anyway. But I think the problem setup is relevant to EA community, because it is a group of agents who, we might assume, often think in similar way, and it is intractable for them to coordinate what actions each individual should take.
And, at least in some interpretations, Sam Bankman-Fried clearly demonstrated what happens when one starts doing expected utility maximization in a completely risk-neutral way.