Introduction

In this post, we describe a generalization of Markov decision processes (MDPs) and partially observable Markov decision processes (POMDPs) called crisp supra-MDPs and supra-POMDPs. The new feature of these decision processes is that the stochastic transition dynamics are multivalued, i.e. specified by credal sets. We describe how supra-MDPs give rise to crisp causal laws, the hypotheses of infra-Bayesian reinforcement learning. Furthermore, we discuss how supra-MDPs can approximate MDPs by a coarsening of the state space. This coarsening allows an agent to be agnostic about the detailed dynamics while still having performance guarantees for the full MDP. 

Analogously to the classical theory, we describe an algorithm to compute a Markov optimal policy for supra-MDPs with finite time horizons. We also prove the existence of a stationary optimal policy for supra-MDPs with infinite time horizons and geometric time discount. Furthermore, we explain the connection between supra-MDPs and stochastic games and summarize known regret bounds. We conclude by showing that crisp supra-POMDPs are equivalent to crisp causal laws.

Supra-Markov Decision Processes

Defining supra-MDPs

To motivate the generalization of MDPs using infra-Bayesianism, we consider a toy problem about the conservation of a Sumatran tiger population.^[1] The population is either locally extinct or extant, and a conservation group that knows the status of the population can annually choose between managing the population with an anti-poaching strategy and doing nothing in order to divert resources elsewhere.

Suppose that when poaching is low, population dynamics are fairly predictable, and thus extinction probability can be reasonably estimated. On the other hand, when poaching is high, the extinction probability is highly dependent on the connectivity between core subpopulations. This connectivity is difficult to directly estimate and sensitive to factors that change over time such as prey abundance.

For example, the conservationists' best estimate may be that when nothing is done, the extinction probability $p$ is equal to 0.2 for 25% connectivity, whereas $p=0.08$ for 50% connectivity. In this case, it may be reasonable to assume that the connectivity ranges between 25% and 50%, and that similarly, $p$ ranges from 0.08 to 0.2. This range of probabilities can be used to define a credal set. This credal set is a valid hypothesis for the ground truth if the next state starting from extant under the "do nothing" action can be sampled according to some element of the set. 

This model can be formulated as a crisp supra-MDP, formally defined as follows. Recall that given a set $X,$ $\square X$ denotes the set of credal sets over $X.$

Definition: Crisp supra-MDP with geometric time discount
A crisp supra-Markov decision process (supra-MDP) $M$ is a tuple $M=(S,s_0,A,T,L,\gamma )$ where

• $S$ is a set of states,
• $s_0\in S$ is an initial state,
• $A$ is a set of actions, 
• $T:S\times A\to \square S$ is a transition infrakernel,
• $L:S\times A\to [0,1]$ is a loss function, and
• $\gamma \in [0,1)$ is a geometric time discount.

Note that the only difference between an MDP and a crisp supra-MDP is the type of the map $T$ that provides information about the state transitions. 

In the Sumatran tiger example, we have the supra-MDP $M=(S,s_0,A,T,L,\gamma )$ where

• $S=\{\text{extinct},\text{extant}\}$,
• $s_0=\text{extant}$,
• $A=\{m,n\}$ with $m$ for "manage" and $n$ for "do nothing", and 
• $T(\cdot ,m)$ is given by 

 and $T(\cdot ,n)$ is given by 

where the numerical entries denote probabilities (of transitioning from states labeling the rows to states labeling the columns) and intervals denote credal sets. 

Alternatively, Figure 1 summarizes $T$ via a state transition graph. 

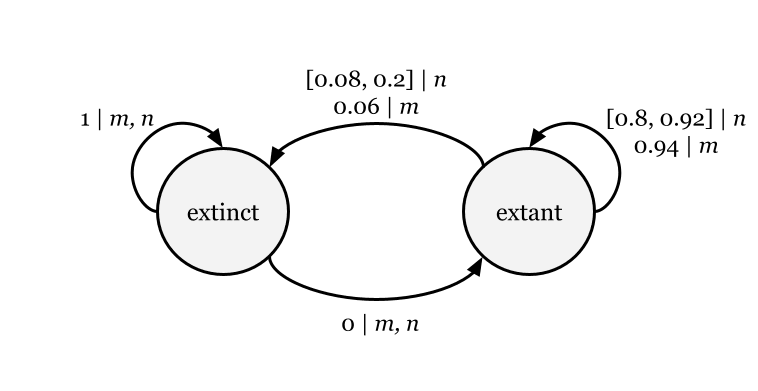
To summarize from a learning theory perspective, a supra-MDP models the following situation. At each time-step, a system is in a state $s\in S.$ The state is known to the agent, who takes an action $a\in A.$ It is assumed that the state transitions stochastically according to some element of the credal set $T(s,a);$ the ground truth is said to satisfy the supra-MDP if this assumption holds. With each state transition, the agent receives loss equal to $L(s,a).$ The goal of the agent during online learning is to minimize the $\gamma$-discounted total loss while under uncertainty about the true state transition dynamics.

Supra-bandits

Recall that a multi-armed bandit is an MDP with one state. Similarly, supra-bandits are a special case of supra-MDPs. In particular, a supra-bandit can be described by a supra-MDP with $S=[0,1]$ where the state encodes the loss obtained from pulling the most recent arm. In this case, the transition kernel, which then takes the form $T:[0,1]\times A\to \square [0,1],$ depends only on the action. The loss $L:S\times A\to [0,1]$ also only depends on the action.

Alternatively, we can equivalently define supra-MDPs so that the type signature of the transition infrakernel is $T:S\times A\to \square (S\times [0,1\left]\right).$ Under this definition, a supra-bandit is a one-state supra-MDP. (We choose the former definition for the transition infrakernel so that the equivalence of supra-MDPs and stochastic games can be explained below more easily.)

Regret bounds for infra-bandits^[2] are studied in Imprecise Multi-Armed Bandits (V. Kosoy). 

Crisp causal laws arising from supra-MDPs and (supra-)RDPs

Recall that a crisp causal law is a map ${\Lambda }_E:\Pi \to \square (A\times O{)}^{\omega }$ generated by a set of environments, meaning that there exists a set of environments $E$ such that ${\Lambda }_E\left(\pi \right)=\overline{\text{ch}\left(\right\{{\mu }^{\pi }:\mu \in E\left\}\right)},$ where $\text{ch}$ denotes convex hull and $\overline{\cdot }$ denotes closure.

Every crisp supra-MDP naturally gives rise to a set of environments, and thus gives rise to a crisp causal law generated by that set of environments. This is possible in two ways: in the more simple case, we assume that $S=O.$ More generally, we can assume the existence of a state representation. In this subsection, we describe both constructions, and also discuss how (supra-)regular decision processes (RDPs) provide state representations. Unlike in the partially observable case (discussed below), not every crisp causal law arises from a supra-MDP. 

With the goal of describing the first case, we define an $M$-copolicy, which is a map $\sigma :(A\times S{)}^{\ast }\times A\to \Delta S$ that is compatible with the transition kernel of a supra-MDP $M=(S,s_0,A,T,L,\gamma ).$ 

Let $ϵ\in (A\times S{)}^{\ast }$ denote the empty string. Define ${\phi }_M:(A\times S{)}^{\ast }\to S$ by ${\phi }_M\left(ϵ\right)=s_0$ and ${\phi }_M\left(has\right)=s$ for nonempty strings $has\in (A\times S{)}^{\ast }$ with prefix $h\in (A\times S{)}^{\ast },$ $a\in A,$ and $s\in S.$

Definition: Copolicy to a supra-MDP

Let $M=(S,s_0,A,T,L,\gamma )$ be a supra-MDP. A map $\sigma :(A\times S{)}^{\ast }\times A\to \Delta S$ is an M-copolicy if for all $h\in (A\times S{)}^{\ast }$ and $a\in A,$ $\sigma (h,a)\in T\left({\phi }_M\right(h),a)$.

If $S=O,$ an $M$-copolicy defines an environment, a map of the form $(A\times O{)}^{\ast }\times A\to \Delta O.$ Thus, a supra-MDP $M$ gives rise to the set of environments that are $M$-copolicies. This set of environments generates a crisp causal law.

Note that in the classical case, i.e. the case when for all $s\in S$ and $a\in A,$  $T(s,a)\in \Delta S,$ there exists a unique copolicy. Thus, an MDP defines an environment. 

The transition dynamics of a crisp supra-MDP are (infra-)Markovian in the sense that the credal set $T(s,a)$ is determined entirely by the current state $s$ and action $a.$ However, in general the copolicy can depend on the history. In turn, the environments compatible with a crisp supra-MDP are not necessarily Markovian. 

State representations

We now consider the more general case in which we have a state representation^[3] given by functions $f:(A\times O{)}^{\ast }\to S$ and $g:(S\times A{)}^{\ast }\times S\to O.$ We require that $f$ and $g$ satisfy a consistency condition. In particular, given a history of states and actions, we can compute the associated history of actions (determined by the given history) and observations (determined by $g)$ in the natural way. To see this formally, define $\hat{g}:(S\times A{)}^{\ast }\times S\to (A\times O{)}^{\ast }$ recursively by

and 

Then we say that $f$ and $g$ are consistent if $f\left(\hat{g}\right(h,s\left)\right)=s$ for all $h\in (S\times A{)}^{\ast }$ and $s\in S.$

In this context, we say that $\sigma :(A\times O{)}^{\ast }\times A\to \Delta S$ is an $M$-copolicy if for all $h\in (A\times O{)}^{\ast }$ and $a\in A,$  $\sigma (h,a)\in T\left(f\right(h),a).$ An $M$-copolicy $\sigma$ defines an environment ${\mu }_{\sigma }$ in the following way. Similarly to the definition of $\hat{g},$ given a history of actions and observations, we can compute the associated history of states (determined by $f)$ and actions (determined by the given history). More precisely, define $\hat{f}:(A\times O{)}^{\ast }\to (S\times A{)}^{\ast }\times S$ recursively by $\hat{f}\left(ϵ\right)=s_0$ where $ϵ$ denotes the empty string and $\hat{f}\left(hao\right)=\hat{f}\left(h\right)af\left(hao\right).$

Given $h\in (A\times O{)}^{\ast }$ and $a\in A,$ let ${\delta }_{\hat{f}\left(h\right)a}$ denote the Dirac delta distribution on $\hat{f}\left(h\right)a\in (S\times A{)}^{\ast }.$ Note that ${\delta }_{\hat{f}\left(h\right)a}\times \sigma (h,a)\in \Delta \left(\right(S\times A{)}^{\ast }\times S).$ Let $g_{\ast }:\Delta \left(\right(S\times A{)}^{\ast }\times S)\to \Delta O$ denote the pushforward of $g.$ Define  ${\mu }_{\sigma }:(A\times O{)}^{\ast }\times A\to \Delta O$ by 

Then $\left\{{\mu }_{\sigma }|\sigma \text{is an}M\text{-copolicy}\right\}$ is a set of environments that generates a crisp causal law.

State representations are naturally induced by regular decision processes (RDPs). RDPs can be viewed in two ways. First, they can be viewed as a special case of POMDPs in which (as explained below) the state can always be deduced from an observation history. An RDP can also be thought of as an MDP that is coupled with a state representation, which is significant as this allows one to define an environment (or, in the supra-case, a crisp causal law).

Definition: Regular decision process (RDP)

A regular decision process (RDP) is a tuple $M=(S,s_0,A,O,T,B,L,\gamma )$ where

• $S$ is a set of states,
• $s_0\in S$ is an initial state,
• $A$ is a set of actions,
• $O$ is a set of observations,
• $L:S\times A\to [0,1]$ is a loss function, and
• $\gamma \in [0,1)$ is a geometric time discount.

Furthermore, 

• $T:S\times A\to \Delta S$ is a transition kernel, and
• $B:S\to O$ is an observation mapping,

which together satisfy that for all $s\in S,$ $a\in A,$ and $o\in O,$ there exists at most one $s^{\prime }\in \text{supp}\left(T\right(s,a\left)\right)$ such that $B\left(s^{\prime }\right)=o$ where $\text{supp}$ denotes support. 

Given an RDP $M,$ the corresponding state representation is defined as follows. We obtain $f_M:(A\times O{)}^{\ast }\to S$ by recursively applying the transition function. In particular, let $f_M\left(ϵ\right)=s_0$ for the empty string $ϵ.$ Given $h\in (A\times O{)}^{\ast },$ $a\in A,$ and $o\in O,$ if there exists $s^{\prime }\in \text{supp}\left(T\right(f_M\left(h\right),a\left)\right)$ such that $B\left(s^{\prime }\right)=o,$ then define $f_M\left(hao\right):=s^{\prime }.$ Otherwise, $f_M\left(hao\right)$ can be defined arbitrarily. Define $g_M:(S\times A{)}^{\ast }\times S\to O$ by $g_M\left(hs\right):=B\left(s\right)$ for all $h\in (S\times A{)}^{\ast }$ and $s\in S.$ 

By replacing the transition kernel with a crisp infrakernel, we can define a crisp supra-RDP. A crisp supra-RDP has all of the data of a crisp supra-MDP, together with the observation mapping that can be used to define a state representation analogously to the classical case. 

Definition: Crisp supra-RDP

A crisp supra-regular decision process (RDP) is a tuple $M=(S,s_0,A,O,T,B,L,\gamma )$ where

• $S$ is a set of states,
• $s_0\in S$ is an initial state,
• $A$ is a set of actions,
• $O$ is a set of observations,
• $L:S\times A\to [0,1]$ is a loss function, and
• $\gamma \in [0,1)$ is a geometric time discount.

Furthermore, 

• $T:S\times A\to \square S$ is a transition infrakernel, and
• $B:S\to O$ is an observation mapping,

which together satisfy that for all $s\in S,$ $a\in A,$ $o\in O,$ and $\theta \in T(s,a),$ there exists at most one $s^{\prime }\in \text{supp}\left(\theta \right)$ such that $B\left(s^{\prime }\right)=o.$ 

In the case when a supra-RDP is given (rather than an RDP), there is more freedom in defining the state representation. Given $h\in (A\times O{)}^{\ast },$ $a\in A,$ and $o\in O,$ define $f_M\left(hao\right):=s^{\prime }$ if there exists $\theta \in T\left(f_M\right(h),a)$ such that $s^{\prime }\in \text{supp}\left(\theta \right)$ and $B\left(s^{\prime }\right)=o.$ Otherwise, $f_M\left(hao\right)$ can be defined arbitrarily as before. Therefore, a crisp supra-RDP can be thought of as a crisp supra-MDP that is coupled with a state representation. 

Approximating an MDP with a supra-MDP 

A supra-MDP can be used to approximate an MDP via a coarsening of the state space. By approximate, we mean that if an MDP is the ground truth, then the ground truth satisfies (is consistent with) the hypothesis that is the supra-MDP. As a result, if a policy for the supra-MDP satisfies some loss bound, then the same bound is guaranteed for the policy interacting with the full MDP. This observation is significant in cases when learning algorithms for MDPs are intractable due to the size of the full state space. Furthermore, the coarsening process allows an agent to be agnostic about parts of the state space that may be difficult to precisely describe.

Consider an MDP $M=(S,s_0,A,T,L,\gamma ).$ Define a surjective coarsening map $c:S\to \tilde{S}$ to a set $\tilde{S}.$ For the coarsening to be nontrivial, $c$ should be non-injective.

Conceptually, the coarsening map allows an agent to be agnostic about the difference between MDP states that are collapsed together. For example, Figure 2 depicts a coarsening in which an MDP with three states is collapsed to a supra-MDP with two states. 

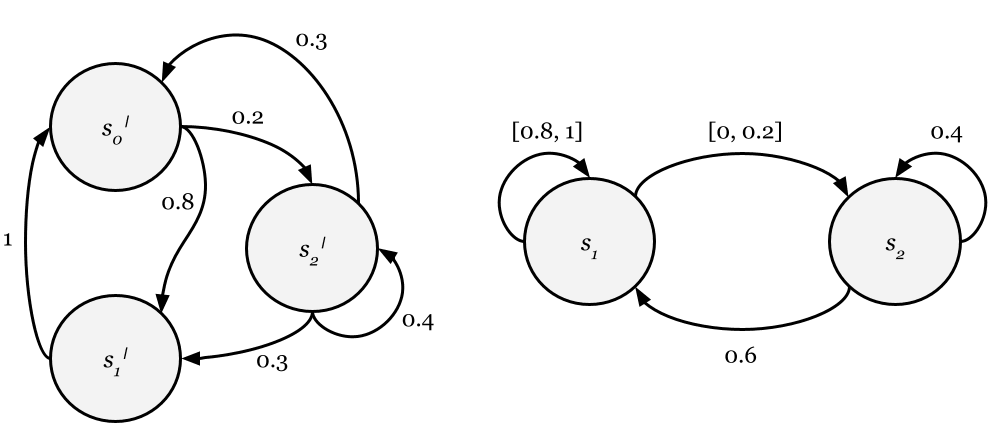
We now define the transition kernel of a supra-MDP with state space $\tilde{S}.$ Recall that the transition kernel of $M$ is of type $T:S\times A\to \Delta S.$ Conceptually, to define the transition infrakernel for a coarsened state $s$, we take the preimage of $s$ under the coarsening map, apply the transition kernel from the full MDP, obtain a credal set by taking the convex closure, and then project back to $\square \tilde{S}$ using the coarsening map. More precisely, let $\text{ch}$ denote convex hull, $\overline{\cdot }$ denote closure, and $c_{\ast }:\square S\to \square \tilde{S}$ denote the pushforward of $c$  extended to credal sets. Define the transition infrakernel $\tilde{T}:\tilde{S}\times A\to \square \tilde{S}$ by 

If the full state space is finite, then each credal set $\tilde{T}(s,a)$ is the closed convex hull of a finite number of points in $\Delta \tilde{S}$ (itself a probability simplex) and thus is isomorphic to a closed convex polytope given by a vertex representation. When a transition infrakernel has this special property, the supra-MDP is said to be polytopic.

Computing the Markov optimal policy for finite time horizons

A policy is said to be Markov if it depends on the state and time-step, but not on the history. If the time horizon is finite, there is an efficient algorithm to compute a Markov optimal policy for a special class of supra-MDPs. In particular, we require that for all $s\in S$ and $a\in A,$ there exists an efficient algorithm to maximize a linear functional over the credal set $T(s,a).$ For example, this holds for polytopic supra-MDPs. 

To compute the optimal policy, we iterate backwards from the final time-step $N.$ Given a state $s\in S,$ define the cost at time $N$ to be the minimal achievable loss, i.e. $C(s,N):={min}_{a\in A}L(s,a).$ We define the policy at time-step $N$ to achieve this minimal loss in every state. More precisely, let $\pi :S\times \{0,\dots ,N\}\to A$ and define

Define the cost of state $s$ at time-step $n<N$ by

Informally speaking, the transition kernel associates every state and action to a credal set of distributions over next states. Then $C(s,n)$ is the minimax expected cost at the next time-step; in particular, it is the best case expected cost over actions and worst case expected cost over the credal set. 

By assumption, there exists an algorithm to maximize a linear functional over $T(s,a)$ for all $s\in S$ and $a\in A$, and thus $C(s,n)$ is computable. Define $\pi$ to achieve $C(s,n),$ i.e. 

Then $\pi$ is an optimal policy, and furthermore it is Markov. 

Existence of stationary optimal policy

A policy is said to be stationary if it depends only on the current state, meaning it has no dependence on the history or time-step. A stationary optimal policy always exists for an MDP. We have the following analogous result for supra-MDPs. 

Proposition 1 [Alexander Appel (@Diffractor), Vanessa Kosoy (@Vanessa Kosoy)]: Let $M=(S,s_0,A,O,T,B,L,\gamma )$ be a crisp supra-MDP with geometric time discount such that $S$ and $A$ are finite. Then there exists a stationary optimal policy.

The detailed proof is contained in the proof section. The key idea is that given any policy, expected loss can only decrease by switching at some time to the policy that is optimal for the current state. A stationary optimal policy is obtained by iteratively applying this argument to an optimal policy. 

The proof relies on the fact that expectation with respect to a credal set can be written in an iterated form. The iterated form comes from the observation that given any finite time-step $n,$ the set of destinies can be decomposed into sets of destinies that are the same up to time $n.$ To be more precise, given a history^[4] $h\in (A\times S{)}^{\ast }$, let $h(A\times S{)}^{\omega }$ denote the set of destinies with prefix $h.$ Let $(A\times S{)}^n\subset (A\times S{)}^{\ast }$ denote the set of histories of length $n.$ Then for any time $n$, the set of destinies can be decomposed into a finite, disjoint union of sets 

Given a policy $\pi :(A\times S{)}^{\ast }\rightharpoonup A,$ let ${\pi }^n$ denote the partial policy obtained by restricting $\pi$ to the first $n$ time-steps. More specifically, let $(A\times O{)}^{\le n}$ denote the set of histories of length at most $n.$ Then ${\pi }^n=\pi {|}_{(A\times O{)}^{\le n}}.$ Furthermore, let ${}^h\pi$ denote the continuation of $\pi$ after a history $h,$ i.e. ${}^h\pi =\pi {|}_{h(A\times S{)}^{\ast }}$ where $h(A\times S{)}^{\ast }$ denotes the set of histories with prefix $h.$ 

Given a crisp causal law $\Lambda ,$ we restrict $\Lambda$ in the natural way to obtain ${\Lambda }^n\left({\pi }^n\right)\in \square (A\times S{)}^n$ and ${\Lambda }^h{(}^h\pi )\in \square (h(A\times S{)}^{\omega })$ where $h$ is a history of length $n.$ Then using the decomposition above, the supra-expectation can be written (in a manner reminiscent of Fubini's Theorem) as

Interpreting supra-MDPs as stochastic games

Every supra-MDP can be interpreted as a zero-sum single controller stochastic game. A stochastic game is a game with a set of states in which after each turn, the game transitions to a new state according to a distribution that depends on the current state and the actions taken by the players in it. If only one player influences the state transitions, the game has the single-controller property. The payoff of the players similarly depends on the state and actions. In a zero-sum game, the gain of one player is the loss of the other. See, e.g. Regret Minimization Algorithms for Single-Controller Zero-Sum Stochastic Games (G. Peng, M. Raginsky, R. Willett, and D. Zois) for a study of strategies for this type of game.

To introduce notation parallel to our definition of a supra-MDP, we formally define zero-sum single-controller games as follows.^[5]

Definition: Zero-sum single-controller game

A zero-sum single-controller stochastic game is a tuple $(S,s_0^{\prime },A_1,A_2,T,K,L)$ where

• $S$ is a set of states,
• $s_0^{\prime }\in S$ is an initial state,
• $A_1$ is the action set of Player 1,
• $A_2$ is the action set of Player 2, 
• $T:S\times A_1\to A_2$ is a function that returns for each $s\in S$ and $a\in A_1$, a set of actions available to Player 2 in the turn,
• $K:S\times A_2\to \Delta S$ is a state transition kernel, and
• $L:S\times A_1\times A_2\to [0,1]$ is a loss function that Player 1 aims to minimize and Player 2 aims to maximize. 

Consider a supra-MDP $M=(S,s_0,A,T,L,\gamma ).$ Let $S=S,$ $s_0^{\prime }=s_0,$ and $A_1=A.$ In the corresponding game, Player 2 ("Nature", or "Murphy"^[6]) controls the transition dynamics in a manner consistent with the transition kernel $T.$ More precisely, let $A_2=\Delta S,$ and $T=T.$ As a consequence, the action set of Player 2 in each turn is restricted by the transition kernel of the MDP.  Define the transition kernel of the game $K:S\times \Delta S\to \Delta S$ to simply return the second argument, i.e. $K(s,\theta )=\theta .$ Furthermore, let $L(s,a,\theta )=L(s,a).$

Using the notation of the supra-MDP, the game has the following protocol. Both players observe the state, which is initialized as $s=s_0.$ Player 1 selects an action $a\in A.$ Then Player 2 adversarially selects a distribution $\theta \in T(s,a).$ More specifically, constrained by a given $s\in S$ and $a\in A,$ Player 2 selects ${\text{argmax}}_{\theta \in T(s,a)}{E}_{s^{\prime }\sim \theta }\left[{min}_{a^{\prime }\in A}L\right(s^{\prime },a^{\prime }\left)\right].$ Player 1 receives loss $L(s,a)$ (and Player 2 receives an equal reward). The next state is sampled according to $\theta .$

If the supra-MDP is polytopic, then without loss of generality the corresponding game can be reduced to a game in which $A_2$ is finite. This is true because if $T(s,a)$ is the closed convex hull of a finite number of distributions $\{{\theta }_0,\dots ,{\theta }_n\}\subseteq \Delta S,$ 

Since we assume that the transition dynamics of $M$ are unknown to the agent, the corresponding game is unknown (as opposed to informed), meaning that Player 1 does not observe the actions of Player 2. As discussed in the next section, this interpretation of supra-MDPs as stochastic games is significant because regret bounds for this class of games can be understood as regret bounds for supra-MDPs.

Regret bounds for episodic supra-MDPs

A supra-MDP is episodic with horizon $H$ if the state is guaranteed to transition to the initial state at the $H$-th time-step. In other words, the supra-MDP resets back to the initial state after each episode of length $H$.

In Online Learning in Unknown Markov Games, Tian et al. propose an online learning algorithm for episodic games of the type discussed in the previous section. The regret bound for this algorithm thus can be applied to supra-MDPs. The notion of regret in this work compares the expected reward of a policy and the minimax value or expected reward of Player 1 at Nash equilibrium. Tian et al. show that it is possible to achieve sublinear regret in this setting by a computationally efficient algorithm. In particular, the regret bound of $\tilde{O}\left(H^2\sqrt[3]{3|S||A|E^2}\right)$ scales with the number of states $|S|$, the number of actions $|A|$, the horizon $H$, and the number of episodes $E.$

This regret bound was improved to $\tilde{O}\left(H\sqrt{|S{|}^3|A|E}\right)$ by Appel and Kosoy as a special case in Regret Bounds for Robust Online Decision Making. Whether or not there exists a computationally efficient algorithm with a regret bound of $\tilde{O}\left(\text{poly}\right(H,|S|,|A|\left)\sqrt{E}\right)$ remains an open problem.

Supra-Partially Observable Markov Decision Processes

In a (supra-)MDP, the state is observed at each time-step. By contrast, in a (supra-)POMDP, an agent only accesses a set of observations. To account for this, a (supra-)POMDP has the additional structure of an observation mapping from states to observations. Similarly to the supra-MDP case, the transition dynamics are Markovian and multivalued. Uncertainty about the initial state is also described by a credal set. We define supra-POMDPs formally as follows.

Definition: Crisp supra-POMDP with geometric time discount

A crisp supra-partially observable Markov decision process (supra-POMDP) is a tuple $(S,{\theta }_0,A,O,T,B,L,\gamma )$ where

• $S$ is a set of states,
• ${\Theta }_0\in \square S$ is an initial credal set over states,
• $A$ is a set of actions,
• $O$ is a set of observations,
• $T:S\times A\to \square S$ is a transition infrakernel,
• $B:S\to O$ is an observation mapping,
• $L:S\times A\to [0,1]$ is a loss function^[7], and
• $\gamma \in [0,1)$ is a geometric time discount.

One might expect the observation map to have range $\square O$ since POMDPs are typically defined to have a stochastic observation map. These formulations are equivalent since the state space can always be replaced by a state space that encodes observations as part of the state, i.e. $S^{\prime }=S\times O.$

Equivalence of crisp causal laws and crisp supra-POMDPs

Crisp causal laws naturally give rise to supra-POMDPs, and vice versa. The following proposition and the commutative diagram in Figure 3 make this equivalence explicit.

Proposition 2: Every crisp causal law specifies a crisp supra-POMDP via a map $\phi .$ Furthermore, every crisp supra-POMDP specifies a crisp causal law via a map $\psi$. For all laws $\Lambda ,$ $\psi \circ \phi \left(\Lambda \right)=\Lambda .$

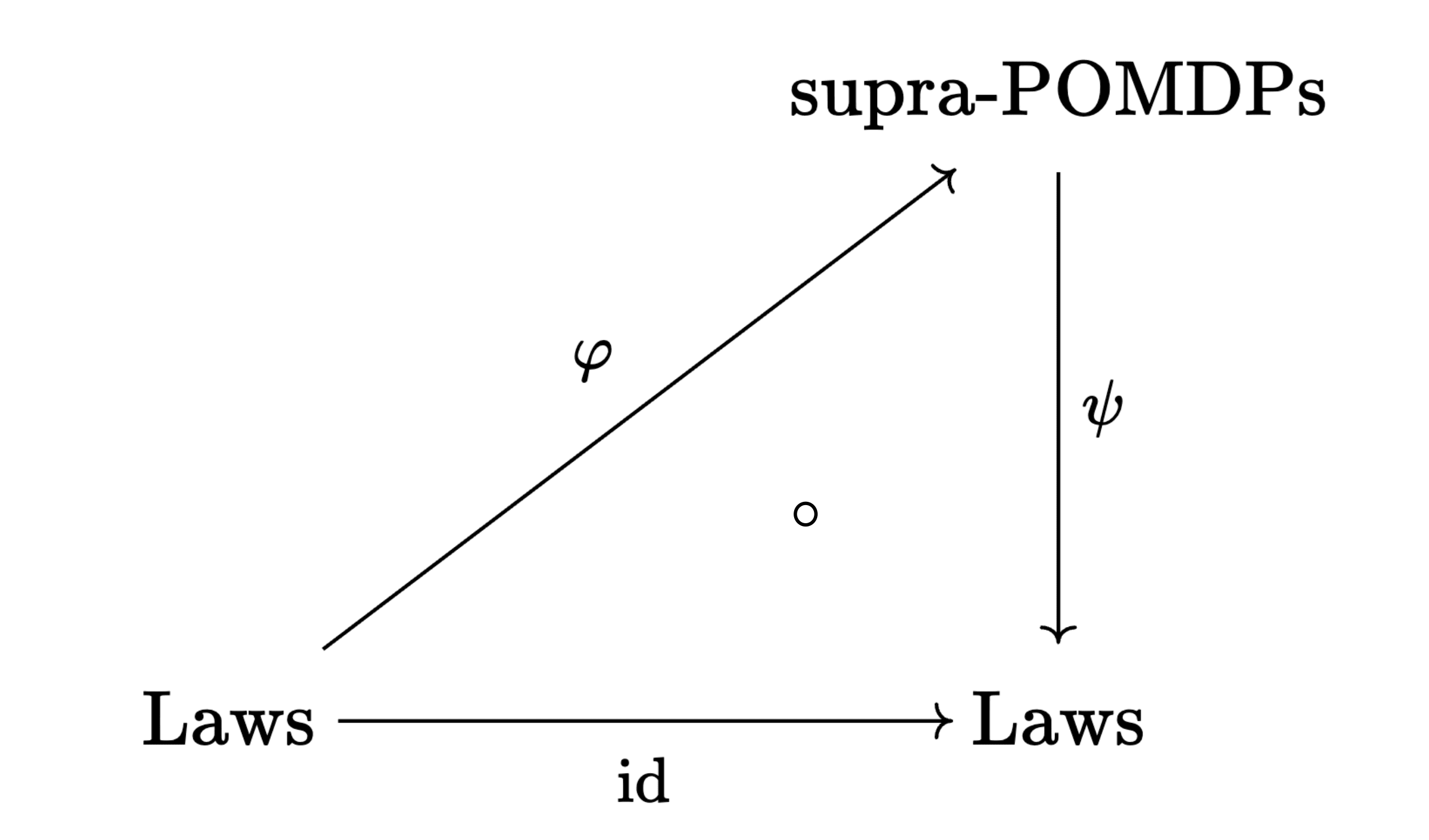
We include a proof of Proposition 2 in the next section in order to illustrate the ideas of an environment compatible with a law and a copolicy to a supra-POMDP. 

Proof of Proposition 2

First we define $\phi$. Let $\Lambda$ denote a crisp causal law. Recall that given an environment $\mu$ and a policy $\pi ,$ ${\mu }^{\pi }\in \Delta (A\times O{)}^{\omega }$ denotes the distribution on destinies determined by the interaction of the policy with the environment.

Definition: Environment compatible with a law

An environment $\mu :(A\times O{)}^{\ast }\times A\to \Delta O$ is compatible with a crisp causal law $\Lambda :\Pi \to \square (A\times O{)}^{\omega }$ if for all $\pi \in \Pi ,$ ${\mu }^{\pi }\in \Lambda \left(\pi \right).$ If $\mu$ is compatible with $\Lambda ,$ we write $\mu ⪯\Lambda .$

Let $E:=\{\mu |\mu ⪯\Lambda \}.$^[8] Note that $E$ is convex and closed. Let $S:=E\times (A\times O{)}^{\ast }$. So, the supra-POMDP we will construct has states that are environments together with a recorded history. 

Let $ϵ$ denote the empty history. Define the initial credal set over states as ${\Theta }_0:={\top }_{E\times \left\{ϵ\right\}}=\Delta (E\times ϵ).$ This credal set captures Knightian uncertainty with respect to the entire set of environments. 

Define the observation mapping $B:E\times (A\times O{)}^{\ast }\to O$ to simply return the most recent observation in the history, i.e. $B(\mu ,hao):=o.$ Note that $B(\mu ,ϵ)$ can be chosen arbitrarily.

We now define the transition infrakernel. Towards that end, for a fixed history $h\in (A\times O{)}^{\ast }$ and action $a\in A,$ define $f_{\mu ,h,a}\left(o\right):O\to S$ to be a function that appends observations to the argument of the state that keeps track of the history, i.e. $f_{\mu ,h,a}\left(o\right)=(\mu ,hao)$. Let $(f_{\mu ,h,a}{)}_{\ast }:\Delta O\to \Delta S$ denote the pushforward of $f_{\mu ,h,a}$. Then define the transition infrakernel to be $T\left(\right(\mu ,h),a):=\left(f_{\mu ,h,a}{)}_{\ast }\mu \right(h,a).$ Note that here we use the natural embedding of $\Delta S$ in $\square S.$

We now discuss how a crisp supra-POMDP $M=(S,{\Theta }_0,A,O,T,B,L,\gamma )$ determines a crisp causal law using copolicies.

Definition: Copolicy to a supra-POMDP

Let $M=(S,{\Theta }_0,A,O,T,B,L,\gamma )$ be a supra-POMDP. A map $\sigma :(S\times A{)}^{\ast }\to \Delta S$ is an $M$-copolicy if

1.  $\sigma \left(ϵ\right)\in {\Theta }_0$ for the empty string $ϵ,$ and
2. For all non-empty strings $hsa\in (S\times A{)}^{\ast }$, $\sigma \left(hsa\right)\in T(s,a)$. 

Informally speaking, a copolicy is a map from state-action strings to distributions over next states that is consistent with the transition infrakernel. A copolicy $\sigma$ together with the observation mapping $B:S\to O$ induces an environment ${\mu }_{\sigma }:(A\times O{)}^{\ast }\times A\to \Delta O$. Let

Define $\psi \left(M\right)$ to be the crisp causal law generated by $E_M$. If $E$ generates the law $\Lambda$, then $\text{ch}\left(\overline{E}\right)=E_{\phi \left(\Lambda \right)}$, and thus for all laws $\Lambda ,$ $\psi \left(\phi \right(\Lambda \left)\right)=\Lambda .$ $\square$

Acknowledgements

I'm grateful to Vanessa Kosoy and Alexander Appel for insightful discussions, and Marcus Ogren and Mateusz Bagiński for their valuable feedback on the initial draft.

1. ^{^}

   This toy example is based on When to stop managing or surveying cryptic threatened species (I. Chadès, E. McDonald-Madden, M. A. McCarthy, B. Wintle, M. Linkie, H. P. Possingham).

2. ^{^}

   Infra-bandits and supra-bandits are distinguished by whether expectation (of a reward function or a loss function respectively) is defined by an infimum or a supremum.

3. ^{^}

   See, e.g. State Representation Learning for Control: An Overview (T. Lesort, N. Díaz-Rodríguez, J. Goudou, D. Filliat) for an introduction to state representation learning, the problem of learning a map from a history of interactions (e.g. actions and observations) to states.

4. ^{^}

   Since the states of a supra-MDP are observable, this terminology is consistent with the previous usage.

5. ^{^}

   These games can be defined more broadly; cf.  Regret Minimization Algorithms for Single-Controller Zero-Sum Stochastic Games (G. Peng, M. Raginsky, R. Willett, and D. Zois). 

6. ^{^}

   This name references Murphy's Law and the infra-Bayesian decision rule. 

7. ^{^}

   Whenever relevant (such as below where $S$ is a compact Polish space), we assume that $L$ is continuous.

8. ^{^}

   Alternatively, we could define $E$ to be a set of environments that generates $\Lambda ,$ which exists by definition but is not unique.