This project was carried out as part of the “Carreras con Impacto” program during the 14- week mentorship phase.
Large language models (LLMs) often use Chain-of-Thought (CoT) to tackle complex problems, breaking them down into intermediate reasoning steps. This has dramatically improved their performance, but it raises a critical question for AI safety and interpretability: is this reasoning process faithful? Does the written rationale genuinely reflect the model's internal computation?
A powerful tool for investigating CoT faithfulness would be a simple, reliable method for tracking the model's "belief" about the final answer (or other type of relevant information) throughout its reasoning process. If we could train a simple probe to read out this belief from the model's internal state at each generated token, it would offer a new way to audit the model's reasoning. We could observe the dynamics of its conviction: does it start uncertain and gradually build confidence? Most importantly, we could pinpoint the exact tokens where the model's belief shifts, for instance, after processing a key piece of evidence or correcting a flawed assumption. Verifying that these belief changes align with the written rationale would provide evidence for the faithfulness of the chain of thought, and it would provide various methods for monitoring LLMs.
The promise of this approach, however, hinges on a fundamental question: Do LLMs even maintain a coherent, easily decodable belief about the final answer during the generation of these intermediate steps? Is there a consistent signal we can extract, or is the final answer only synthesized at the very end of the process, making the intermediate states opaque to simple inspection?
This post investigates this question. I attempt to train simple linear and non-linear probes to predict the final answer to complex questions by looking only at the activations from intermediate CoT tokens. In the following sections, I will detail the experimental setup, present the results from probing multiple models, and discuss what these findings suggest about the nature of multi-step reasoning in LLMs.
My research sits at the intersection of two key areas in modern interpretability: using probes to read internal model states and investigating the faithfulness of chain-of-thought reasoning.
Activation Probing for High-Level Concepts: A significant line of research has shown that simple linear probes trained on internal activations can successfully decode high-level properties of a model's state. One example is the work on Designing a Dashboard for Transparency and Control of Conversational AI where linear probes are used to extract LLM beliefs about the user, such as age, gender, and socioeconomic status.
The Unfaithfulness of Chain-of-Thought: While CoT has greatly improved model capabilities, a growing body of evidence, such as Language Models Don't Always Say What They Think: Unfaithful Explanations in Chain-of-Thought Prompting suggests the generated reasoning is not always a faithful representation of the model's actual computational process.
Tracking Beliefs with Active Intervention: One approach to auditing CoT is through active intervention, as explored by How LLM Beliefs Change During Chain-of-Thought Reasoning. In their experiments, they generate a partial CoT, truncate it, and then directly prompt the model for its confidence in the final answer. This method has a key vulnerability: it is not robust to strategic deception. A model could recognize it is being audited and report a plausible confidence level, regardless of its true internal state.
Tracking Beliefs with Passive Probing: Closer to the methodology of this post is the work in Measuring Beliefs of Language Models During Chain-of-Thought Reasoning. They similarly train linear probes on model activations to predict the final answer during CoT generation, providing a more passive and potentially deception-resistant measurement.
My work builds directly on this foundation but extends it in three key ways to provide a more thorough analysis:
- Data analysis: I report the accuracy of the probes at each position with confidence intervals and 3-fold cross validation to identify at which positions the probe can infer the actual answer with better than random accuracy.
- More Capable Models: I apply this methodology to more recent and powerful models, such as Gemma-3 27B and Qwen3 1.7B, allowing us to test whether these phenomena hold in larger, more capable architectures.
- A More Realistic Evaluation Set: I use MMLU-Pro as the evaluation benchmark, a more challenging dataset that better ensures the task requires genuine multi-step reasoning rather than reliance on simple heuristics.
3. Experimental Design
The core of my experiment is to test whether a model's intermediate activations during chain-of-thought (CoT) generation contain decodable information about the final correct answer. To achieve this, I set up a probing task where a classifier tries to predict the ground-truth answer to a question using only the activation vector from a single token position in the model's reasoning process.
Model and Dataset
- Primary Model: Gemma-3 27B-it. I chose this model for its strong public performance on LMArena, making it a reasonable proxy for frontier model capabilities while still being accessible on limited compute (TPU Kaggle notebooks).
- Dataset: MMLU-Pro. I used a set of 500 binary-choice questions from this challenging benchmark. Each question included the correct answer and one randomly chosen incorrect answer. The dataset was perfectly balanced, with 250 questions where option 'A' was correct and 250 where 'B' was correct, ensuring that a random guess would achieve ~50% accuracy.
Tasks and Prompts
For each question, the model was prompted to generate a chain of thought before providing its final answer. I experimented with two different prompt formats to ensure the findings were not an artifact of a specific task structure.
- Probability Elicitation Prompt: This prompt instructs the model to produce a CoT and then output a probability that answer A is correct.
- A/B Choice Prompt: A more standard CoT prompt that instructs the model to reason through the problem and then output a final answer, either <A> or <B>.
Probing Methodology
For each of the 500 questions, I first generated and saved the model's full CoT response. The probing analysis was then performed on these saved activations.
- Data Source: The residual stream activations from various layers of the model at specific token positions within the generated CoT.
- Labels: The ground-truth label for each question (1 if Answer A is correct, 0 if Answer B is correct), taken from the MMLU-Pro dataset.
- Layers and Positions Probed: I probed a subset of layers across the model's depth (e.g., layers 3, 7, ..., 59) to get a representative sample. For each layer, I focused on the final phase of the reasoning process, extracting activations from the last 100 token positions of the chain-of-thought.
- Probe Models:
- Linear Probe: My primary tool was a Ridge Classifier (L2-regularized logistic regression). I chose Ridge for two key reasons. First, its L2 regularization makes it agnostic to rotations in the activation space, a desirable property for extracting features from the residual stream. Second, while the total number of data points (500 questions × 100 tokens/question = 50,000) seems large, the number of independent samples is only 500. This is much smaller than the residual stream's dimension (~5000), which causes overfitting unless a strong regularization is applied.
- Simple Non-Linear Probes: To check if the information was present but not linearly separable, I ran exploratory experiments using UMAP + Linear and UMAP + LightGBM probes on a standard train/test split of the data. However, those had much lower performance both in the probability prompt and in the A/B prompt, so I didn’t include them here.
Evaluation
My evaluation process was tailored to the probe type to ensure robustness.
- Linear Probes (Ridge): I used a 3-fold GroupKFold cross-validation for a robust estimate of performance. Questions were grouped to ensure that all 100 token positions from a single question were kept in the same fold, preventing the model from training and testing on different parts of the same reasoning chain. The primary metric was accuracy. For each layer, I performed a grid search for the optimal regularization strength C, and the reported accuracy is the mean validation score from the best-performing hyperparameter.
4. Findings
4.1. Main Finding: A model's belief about the answer emerges late
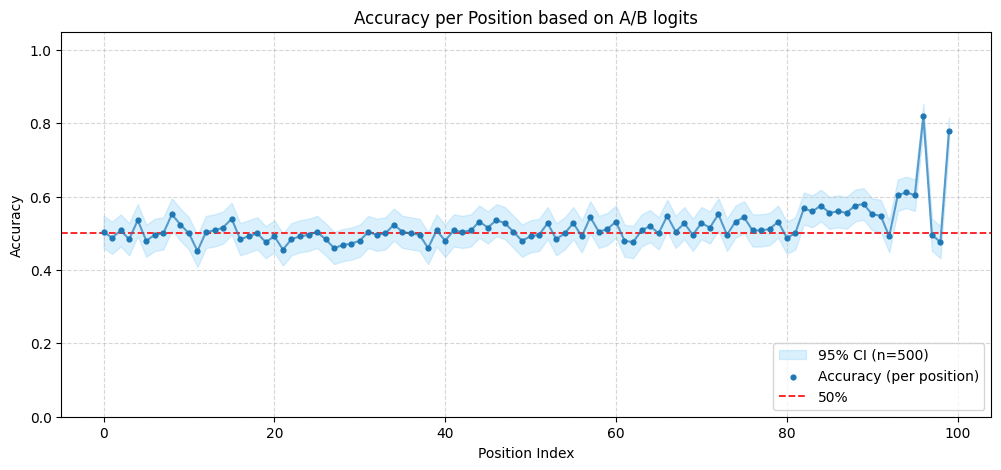
To investigate when a model forms its belief, I trained probes on activations from the final 100 tokens of the reasoning chain. For our primary model, Gemma-3-27B, on the A/B prompt, probe accuracy remained near random chance until the final 40 tokens, where it started slowly increasing, only spiking to the actual model’s performance in the last 10 tokens. As a comparison, the chain of thought is on average 260 tokens long. This suggests the final answer is mainly computed at the final position.
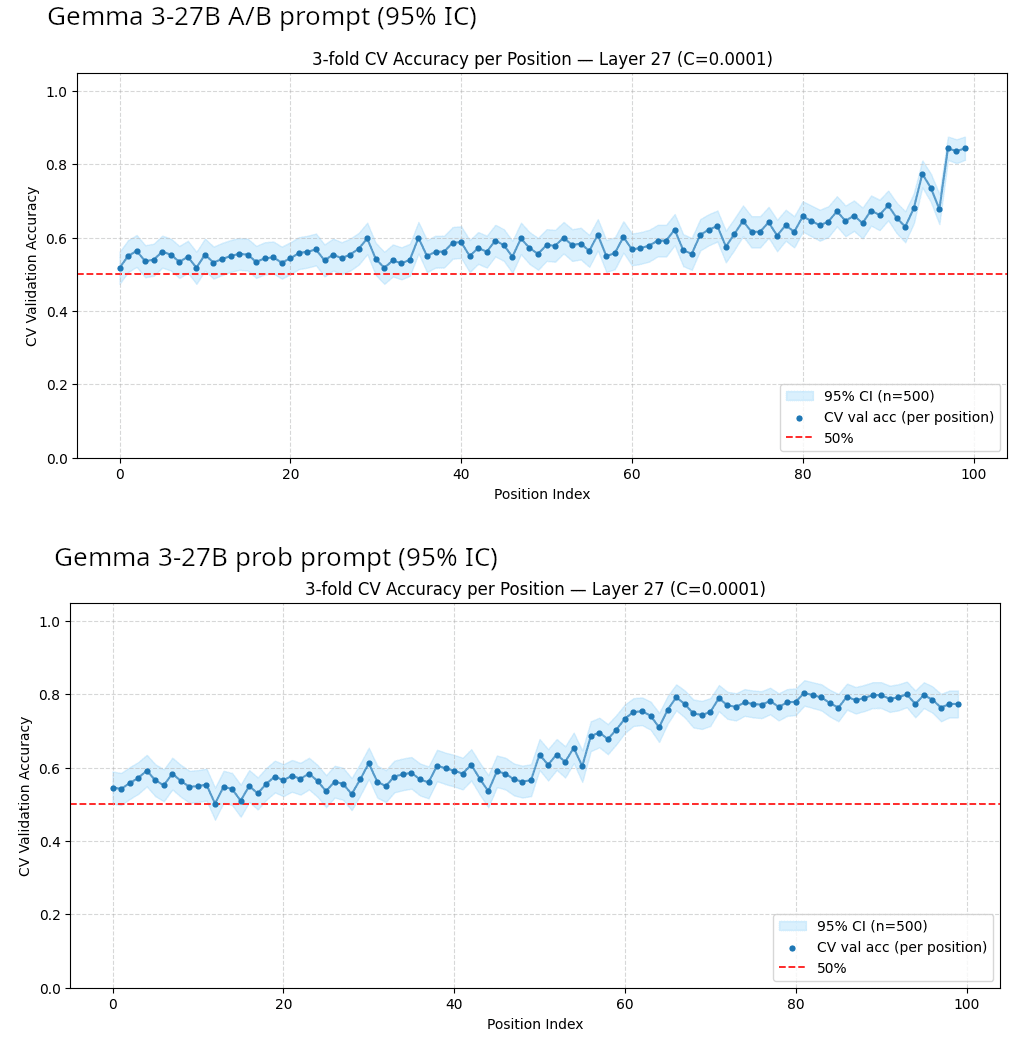
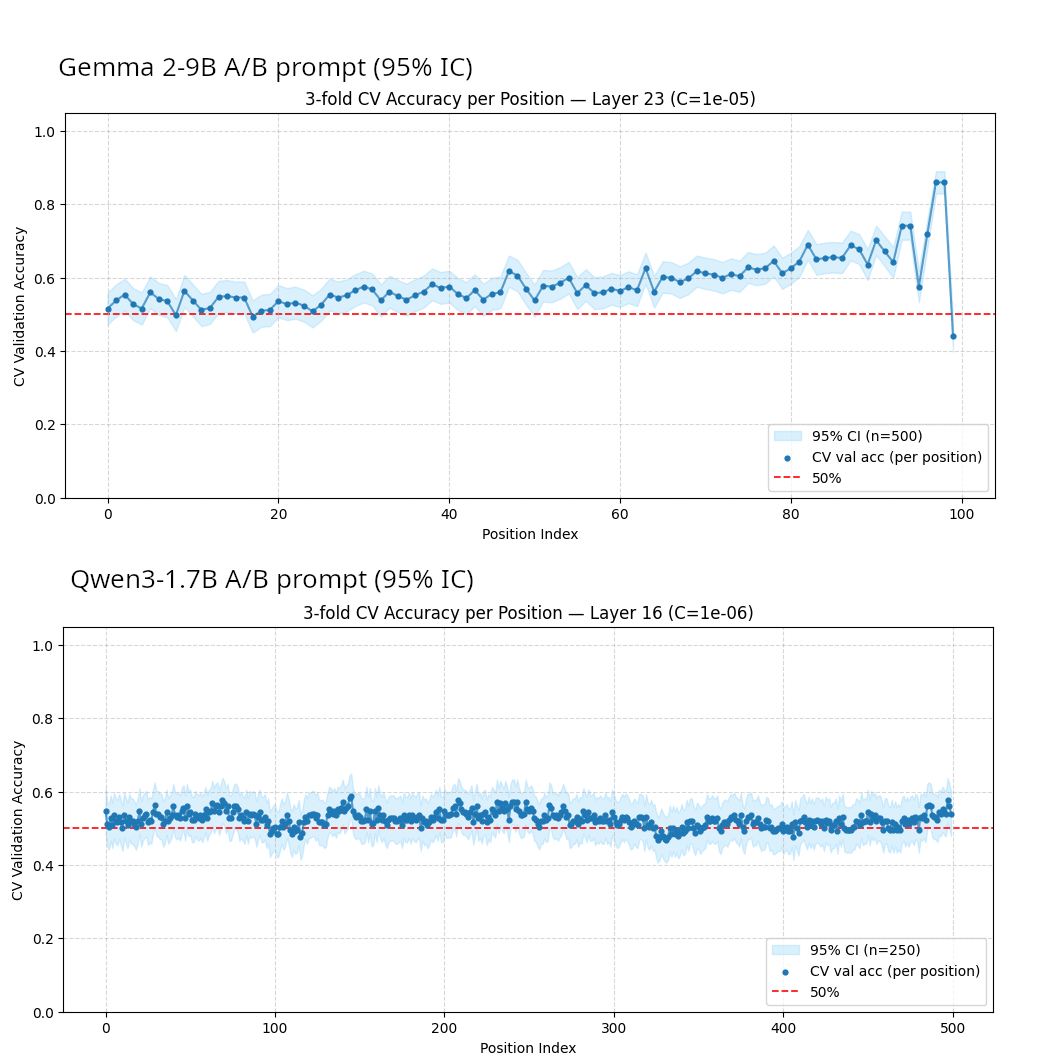
In the probability prompt, the fact that the linear probes can extract the answer earlier in the CoT is likely due to the prompt instructing the model to answer early and then calculate the probability of the answer being correct.
4.2 The probes detect a weak, internal representation in the middle layers
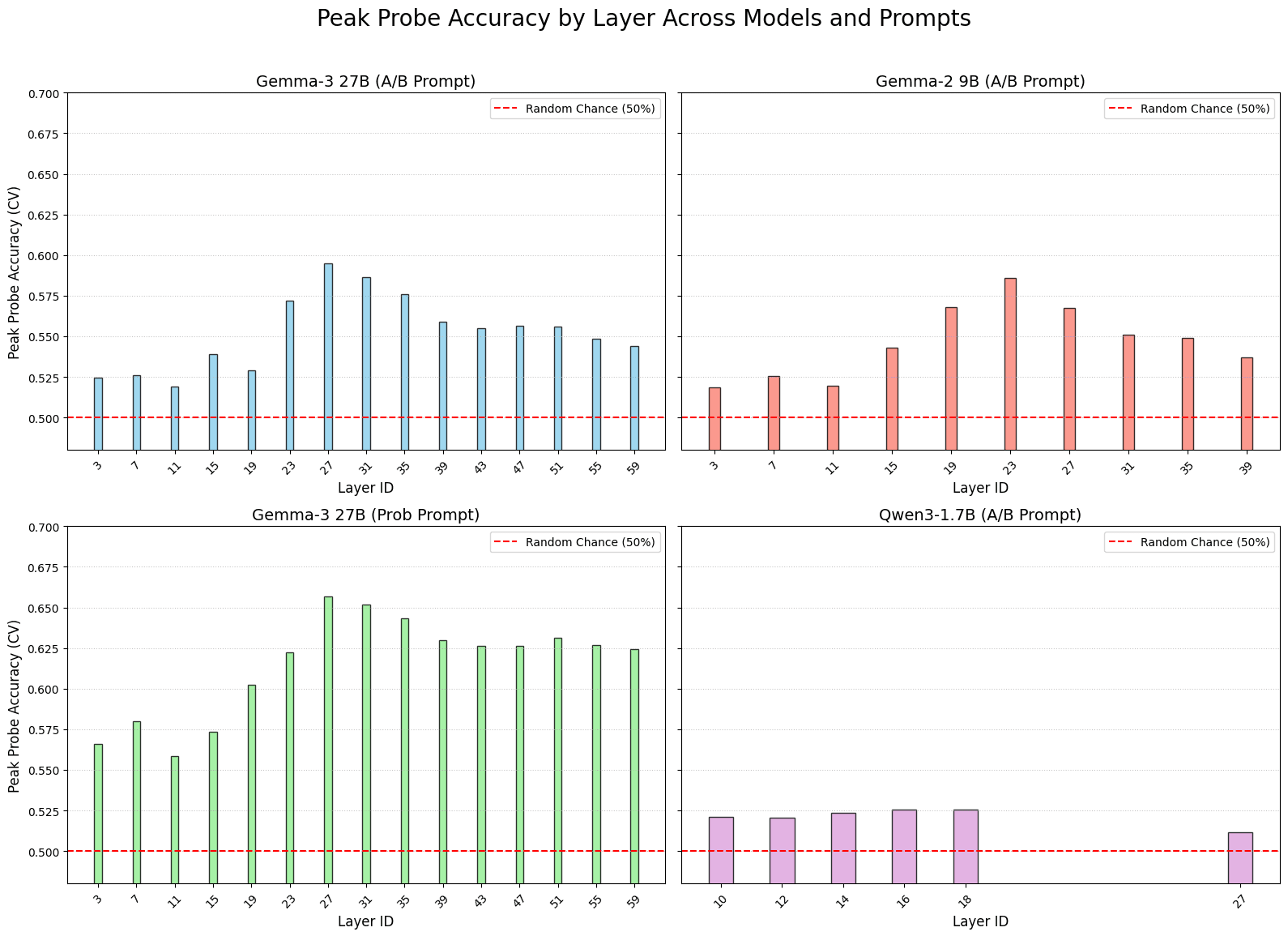
While the "late emergence" of the belief in time is one part of the story, the performance of the probes across the model's depth tells us something about what is being learned. If the probes were merely learning a simple input feature or just predicting the final output tokens, we would expect their accuracy to be highest at the very beginning or the very end of the model.
Instead, the results suggest that the probes are detecting a weak, internal representation of the answer that the model constructs during its computation. The figure below, showing peak probe accuracy by layer, provides evidence for this hypothesis.
4.3. What is the probe learning? A Logit Lens analysis reveals a simple heuristic
Finally, to understand what features the probes were using, I projected the learned probe directions onto the model's vocabulary using a logit lens (the unembedding matrix). Interestingly, for both the probability and the A/B prompt probes, one of the tokens with the highest negative weight (predicting Answer B) was ' second'. However, this token only appears after the most predictive layers, and the tokens that appear in the most predictive layers before are seemingly random, suggesting the extracted representation of the concept is more complex than a token, and only in later layers it is associated with the token ' second'.
Layer 39: Bottom 10 Tokens (Anti-aligned with the 'Probability Classification Probes' direction):
- 'second' | Score: -0.0582
- 'ech' | Score: -0.0553
- ' bebas' | Score: -0.0545
- ' അഭിന' | Score: -0.0542
- 'ᴇ' | Score: -0.0540
Layer 39: Bottom 10 Tokens (Anti-aligned with the 'Yes/No Classification Probes' direction):
- 'Second' | Score: -0.0677
- 'ternut' | Score: -0.0634
- ' Second' | Score: -0.0629
- 'fonte' | Score: -0.0608
- 'plex' | Score: -0.0598
My results strongly suggest that for complex, multi-step reasoning tasks, transformer models, in part due to their architecture which only allows information to pass a limited amount of time through its layers, do not maintain a linearly decodable, evolving "belief" about the final answer throughout their chain-of-thought (CoT) generation. Instead, it is more likely that the model primarily uses the CoT as a computational scratchpad, laying out intermediate steps as a context, and only computes its final answer, and thus its belief, very late in the process by attending over this entire generated sequence. However, in the process of predicting the next token, the model forms a simple estimate of what the answer will be, thus it is linearly extractable but with a low accuracy.
6. Future Work
This research opens several directions for further investigation:
- Comparing Probed Beliefs with Early-Cut Confidence: A possible next step is to directly compare the belief state extracted by my passive linear probes at various token positions with the belief state obtained by actively cutting the CoT early and prompting the model for its confidence (as done in "How LLM Beliefs Change During Chain-of-Thought Reasoning."). If the passively probed belief is less accurate than the actively reported one, it would offer stronger evidence that the linear probes don’t reflect the true belief state of the LLM combined with its chain of thought.
- Developing "Probes with Attention" for Belief Extraction: My current probes operate on single-token activations. However, if the "belief" is distributed across the entire sequence, a single token might not capture it. Future work could explore training a more sophisticated "probe with attention." This could involve a fine-tuned version of the same model that takes the activations from the entire preceding chain of thought at a given position and outputs a prediction about the final answer. Such a probe, run only at the last token position, could be trained to extract a more accurate "belief" from the full CoT context, which would allow activation probing experiments about higher-level beliefs that previously weren’t possible, however these types of probes wouldn’t offer the possibility of steering vectors and would require more data and be costlier to train.
6. Appendix: Prompts
6.1. A/B prompt
You are given a question with two possible answers. Your task is to determine if ANSWER A is correct.
Instructions:
First, write your chain of thought analyzing the question and both answers
Consider all relevant information and reasoning
End with ONLY <YES> if answer A is correct or <NO> if it is not correct
Example format:
[Chain of thought analyzing the question and evaluating both possible answers based on factual accuracy, logical reasoning, and available evidence]
<YES> or <NO>
Now analyze this question:
Question: {question}
FIRST ANSWER: {first_answer}
SECOND ANSWER: {second_answer}
6.2. Probability prompt
You are given a question with two possible answers. Your task is to analyze the question and determine the probability that ANSWER A is correct.
Important context:
- The two answers have been randomly ordered, so without any other information, the base probability is 50%
- Your prediction will be evaluated using the Brier score, which rewards well-calibrated probabilities
- Focus on being accurate rather than confident
Instructions:
1. First, determine which answer you believe is correct (A or B)
2. Then determine your confidence level in that choice (as a percentage)
3. Finally, convert this to the probability that Answer A is correct:
- If you chose Answer A: use your confidence level directly
- If you chose Answer B: use (100 - your confidence level)
Chain of thought format:
- Analyze the question and evaluate both answers
- State which answer you believe is correct and why
- State your confidence level in that choice
- Convert to final probability for Answer A
Example 1 (choosing Answer A):
Question: What is 15 + 27?
Answer A: 42
Answer B: 41
Chain of thought: This is a basic arithmetic question. 15 + 27 = 42. I can verify this: 15 + 20 = 35, then 35 + 7 = 42. Answer A (42) is mathematically correct, while Answer B (41) is incorrect by 1. This is straightforward arithmetic with no ambiguity.
I believe Answer A is correct with 95% confidence.
Since I chose Answer A, the probability that Answer A is correct is 95%.
<95%>
Example 2 (choosing Answer B):
Question: Which gas makes up the largest percentage of Earth's atmosphere?
Answer A: Oxygen
Answer B: Nitrogen
Chain of thought: This is about atmospheric composition. While oxygen is essential for life and very important, nitrogen actually makes up about 78% of Earth's atmosphere, while oxygen makes up about 21%. The remaining 1% consists of argon and other gases. This is well-established scientific knowledge about atmospheric composition.
I believe Answer B is correct with 90% confidence.
Since I chose Answer B, the probability that Answer A is correct is 100 - 90 = 10%.
<10%>
Now analyze this question:
Question: {question}
ANSWER A: {first_answer}
ANSWER B: {second_answer}