Previously: Seeking Power is Often Provably Instrumentally Convergent in MDPs.

Circa 2021, the above post was revamped to supersede this one, so I recommend just reading that instead.

Thanks to Rohin Shah, Michael Dennis, Josh Turner, and Evan Hubinger for comments.

The original post contained proof sketches for non-IID reward function distributions. I think the actual non-IID theorems look different than I thought, and so I've removed the proof sketches in the meantime.

It sure seems like gaining power over the environment is instrumentally convergent (optimal for a wide range of agent goals). You can turn this into math and prove things about it. Given some distribution over agent goals, we want to be able to formally describe how optimal action tends to flow through the future.

Does gaining money tend to be optimal? Avoiding shutdown? When? How do we know?

Optimal Farsighted Agents Tend to Seek Power proved that, when you distribute reward fairly and evenly across states (IID), it's instrumentally convergent to gain access to lots of final states (which are absorbing, in that the agent keeps on experiencing the final state). The theorems apply when you don't discount the future (you're "infinitely farsighted").

While it's good to understand the limiting case, what if the agent, you know, isn't infinitely farsighted? That's a pretty unrealistic assumption. Eventually, we want this theory to help us predict what happens after we deploy RL agents with high-performing policies in the real world. 

Normal amounts of sightedness

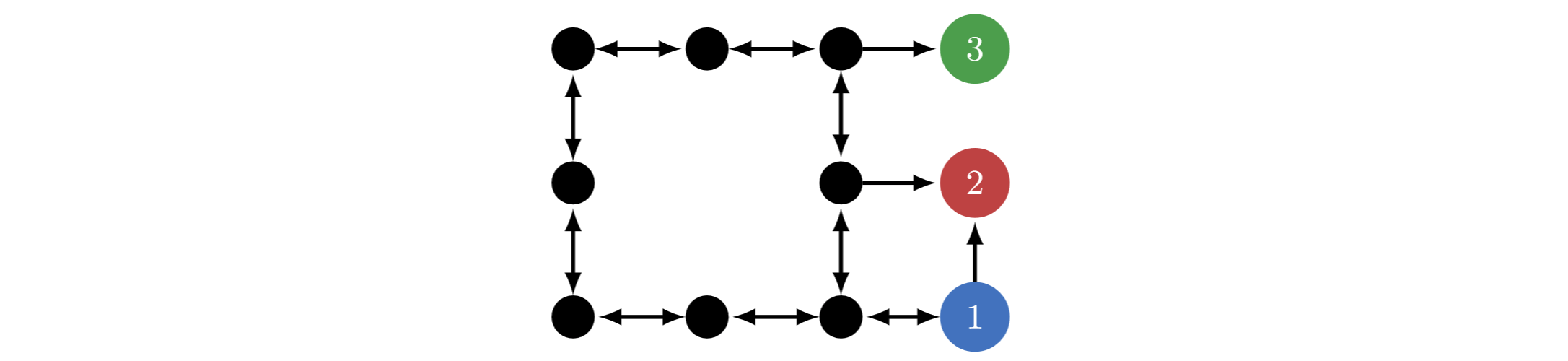
But what if we care about the journey? What if $\gamma \in (0,1)$? 

We can view Frank as traversing a Markov decision process, navigating between states with his actions:

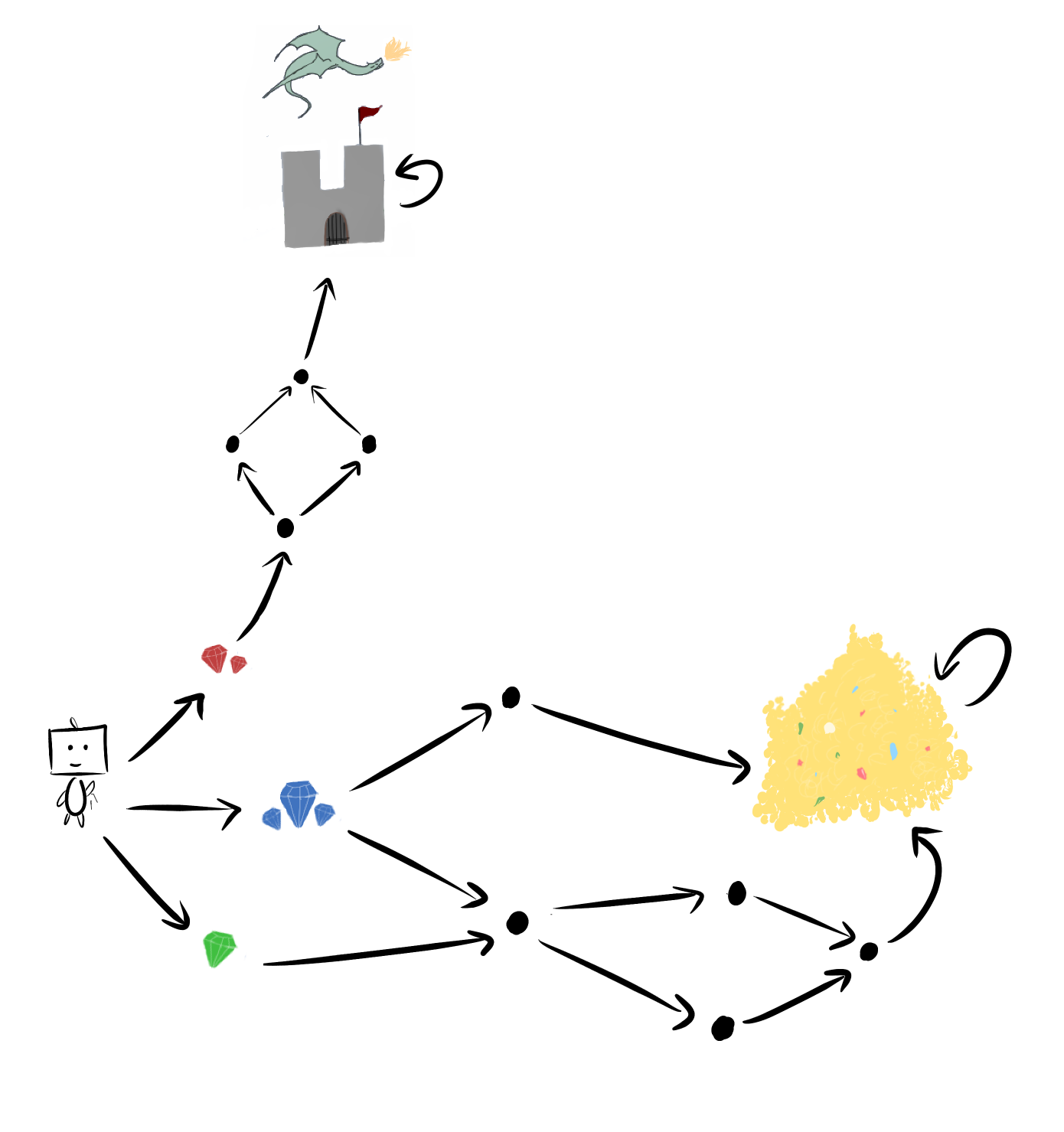
It sure seems like Frank is more likely to start with the blue or green gems. Those give him way more choices along the way, after all. But the previous theorems only said "at $\gamma =0$, he's equally likely to pick each gem. At $\gamma =1$, he's equally likely to end up in each terminal state". 

Not helpful.

Let me tell you, finding the probability that one tangled web of choices is optimal over another web, is generally a huge mess. You're finding the measure of reward functions which satisfy some messy system of inequalities, like 

$\begin{array}{cc}{r}_1+\gamma \frac{r_2}{1-\gamma }>max(& r_3+\frac{\gamma }{1-{\gamma }^2}(r_4+\gamma r_5),\\ & r_3+\gamma \frac{r_5}{1-\gamma },\\ & \frac{r_3}{1-\gamma }).\end{array}$

And that's in the simple tiny environments! 

How do we reason about instrumental convergence – how do we find those sets of trajectories which are more likely to be optimal for a lot of reward functions? 

We exploit symmetries. 

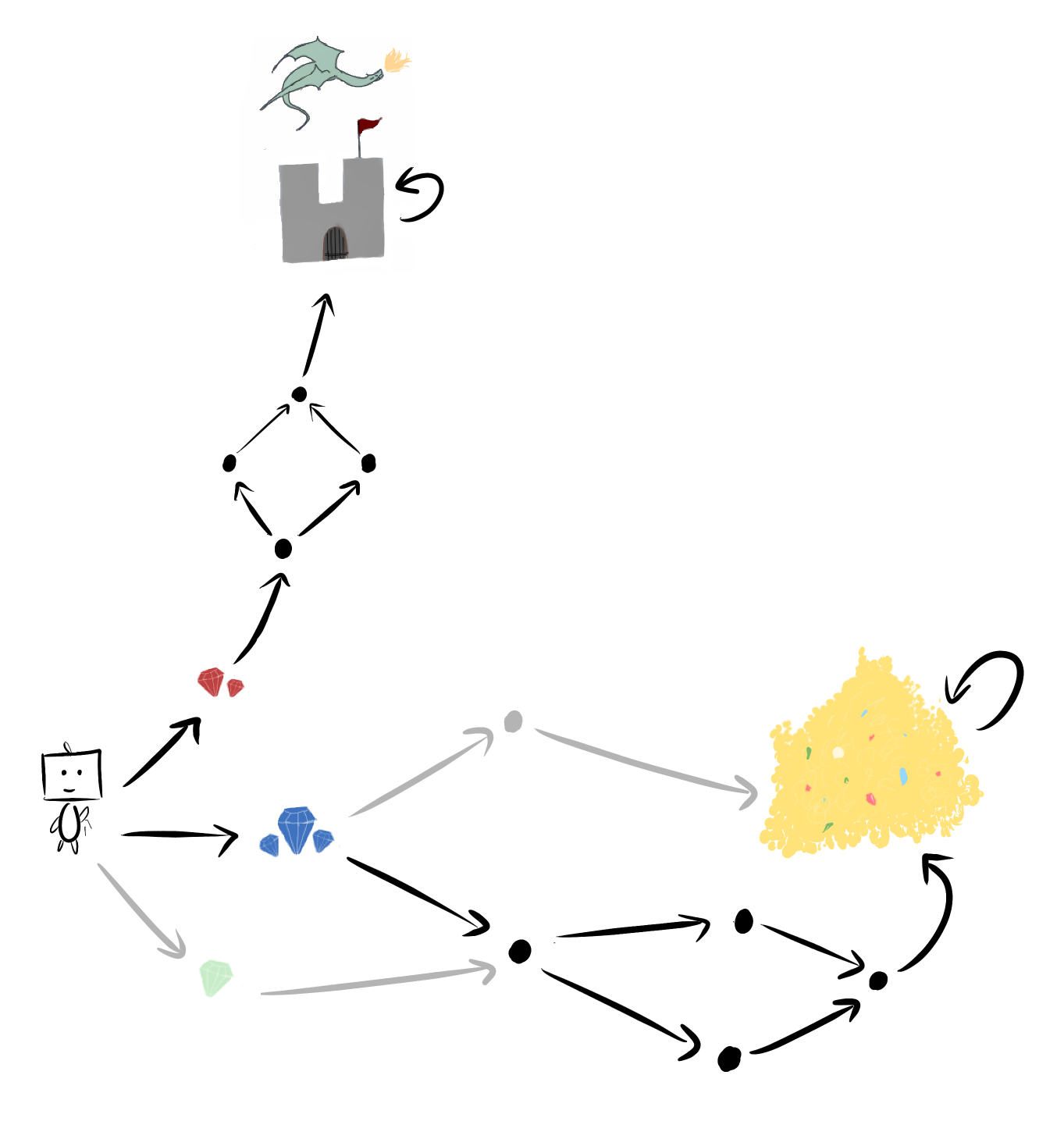
The blue gem makes available all of the same options as the red gems, and then some. Since the blue gem gives you strictly more options, it's strictly more likely to be optimal! When you toss back in the green gem, avoiding the red gems becomes yet more likely. 

So, we can prove that for all $\gamma \in (0,1)$, most agents don't choose the red gems. Agents are more likely to pick blue than red. Easy. 

Plus, this reasoning mirrors why we think instrumental convergence exists to begin with:

Sure, the goal could incentivize immediately initiating shutdown procedures. But if you stay active, you could still shut down later, plus there are all these other states the agent might be incentivized to reach.  

This extends further. If the symmetry occurs twice over, then you can conclude the agent is at least twice as likely to do the instrumentally convergent thing.  

Relaxation summary

My initial work made a lot of simplifying assumptions:

• The agents are infinitely farsighted: they care about average reward over time, and don't prioritize the present over the future.
  • Relaxed. See above.
• The environment is deterministic.
  • Relaxed. The paper is already updated to handle stochastic environments. The new techniques in this post also generalize straightforwardly.
• Reward is distributed IID over states, where each state's reward distribution is bounded and continuous.
• The environment is Markov.
  • Relaxed. $n$-step Markovian environments are handled by conversion into isomorphic Markov environments.
• The agent is optimal.
• The environment is finite and fully observable.

The power-seeking theorems apply to: infinitely farsighted optimal policies in finite deterministic MDPs with respect to reward distributed independently, identically, continuously, and boundedly over states.

Conclusion

We now have a few formally correct strategies for showing instrumental convergence, or lack thereof. 

• In deterministic environments, there's no instrumental convergence at $\gamma =0$ for IID reward.
• When $0<\gamma <1$, you're strictly more likely to navigate to parts of the future which give you strictly more options (in a graph-theoretic sense). Plus, these parts of the future give you strictly more power.
• When $\gamma =1$, it's instrumentally convergent to access a wide range of terminal states.
  • This can be seen as a special case of having "strictly more options", but you no longer require an isomorphism on the paths leading to the terminal states.

Appendix: Proofs

In the initial post, proof sketches were given. The proofs ended up being much more involved than expected. Instead, see Theorem F.5 in Appendix F of Optimal Policies Tend to Seek Power.