Introduction

Imagine if a forecasting platform had estimates for things like:

1. "For every year until 2100, what will be the probability of a global catastrophic biological event, given different levels of biosecurity investment and technological advancement?"
2. "What will be the impact of various AI governance policies on the likelihood of developing safe and beneficial artificial general intelligence, and how will this affect key indicators of global well-being over the next century?"
3. "How valuable is every single project funded by Open Philanthropy, according to a person with any set of demographic information, if they would spend 1000 hours reflecting on it?"

These complex, multidimensional questions are useful for informing decision-making and resource allocation around effective altruism and existential risk mitigation. However, traditional judgemental forecasting methods often struggle to capture the nuance and conditionality required to address such questions effectively.

This is where "scorable functions" come in - a forecasting format that allows forecasters to directly submit entire predictive models rather than just point estimates or simple probability distributions. Scorable functions allow encoding a vast range of relationships and dependencies, from basic linear trends to intricate nonlinear dynamics. Forecasters can precisely specify interactions between variables, the evolution of probabilities over time, and how different scenarios could unfold.

At their core, scorable functions are executable models that output probabilistic predictions and can be directly scored via function calls. They encapsulate the forecasting logic, whether it stems from human judgment, data-driven insights, or a hybrid of the two. Scorable functions can span from concise one-liners to elaborate constructs like neural networks.

Over the past few years, we at QURI have been investigating how to effectively harness these methods. We believe scorable functions could be a key piece of the forecasting puzzle going forward.

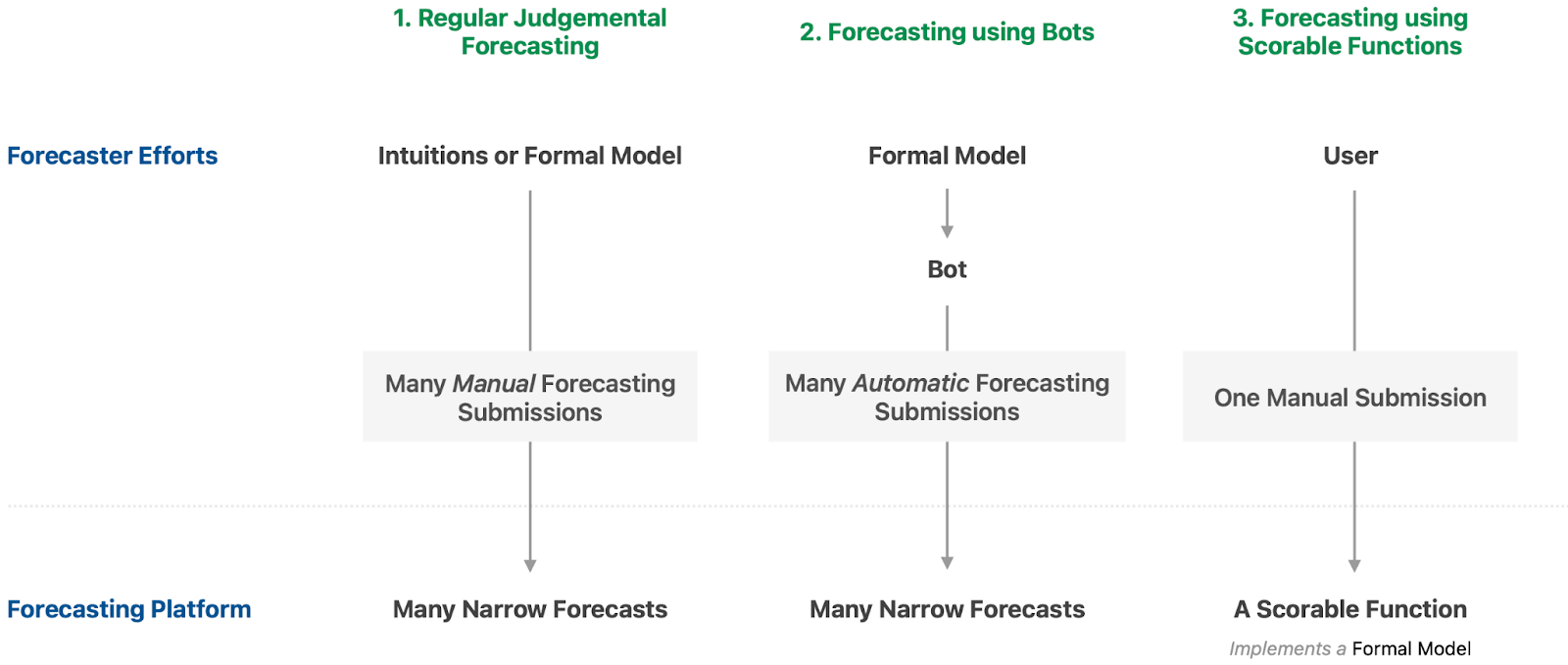
From Forecast Bots to Scorable Functions

Many people are familiar with the idea of using "bots" to automate forecasts on platforms like Metaculus. Let's consider a simple example to see how scorable functions can extend this concept.

Suppose there's a binary question on Metaculus: "Will event X happen in 2024?" Intuitively, the probability should decrease as 2024 progresses, assuming no resolution. A forecaster might start at 90% in January, but want to gradually decrease to 10% by December.

One approach is to manually update the forecast each week - a tedious process. A more efficient solution is to write a bot that submits forecasts based on a simple function:

chanceOfXby2025(current_date) = 0.9 * proportion_of_year_remaining(current_date, 2024)

(Example using Squiggle, but hopefully it's straightforward enough)

This bot can automatically submit daily forecasts via the Metaculus API.

However, while more efficient than manual updates, this approach has several drawbacks:

1. The platform must store and process a separate forecast for each day, even though they all derive from a simple function.
2. Viewers can't see the full forecast trajectory, only the discrete submissions.
3. The forecaster's future projections and scenario contingencies are opaque.

Scorable functions elegantly solve these issues. Instead of a bot submitting individual forecasts, the forecaster simply submits the generating function itself. You can imagine there being a custom input box directly in Metaculus.

The function submitted would be the same, though it might be provided as a lambda function or with a standardized function name.

fn(current_date) = 0.9 * proportion_of_year_remaining(current_date, 2024)

The platform can then evaluate this function on-demand to generate up-to-date forecasts. Viewers see the complete forecast trajectory and can even inspect the function code. The forecaster can update their forecast by simply modifying the function.

Now consider a more complex example:

chanceOfXby2025(current_date, related_forecast) = 0.6 * proportion_of_year_remaining(current_date, 2024) + 0.4 * related_forecast

Here, the forecast depends not only on time, but on the current value of related_forecast, e.g., the probability of a related event. The function encodes the forecaster's view on how these probabilities interact. The forecaster is now submitting a conditional probability directly.

With traditional bots, this kind of complex, conditional forecast would be infeasible. But with scorable functions, it's trivial. Viewers can see how the forecast responds to different scenarios for the related question.

The potential applications are vast. Forecasters could condition on economic indicators, poll results, prediction market prices, and more. Complex, multidimensional forecasts become possible:

recession_probability(country, gdp_history, month_in_question) = ...

This function could output a probability of a recession for each country and month, based on GDP history. Such a forecast would be infeasible with traditional methods, but is straightforward with scorable functions.

Of course, realizing this potential will require careful platform design. But the benefits are substantial. Forecasters can express their knowledge more precisely and efficiently. Viewers gain deeper insight into forecast rationales and contingencies. Platforms can elicit and evaluate more sophisticated forecasts. It can be a win for all parties.

Potential Uses of Scorable Functions

Scorable functions can be applied to a wide range of forecasting questions, making them highly versatile. Here are some examples of questions well-suited for scorable functions:

1. Financial Forecasting:
   • "Create a model that predicts, for any date D (from 2023 to 2033), the closing price of any provided set of financial assets from the stock market on that date."
2. Cryptocurrency Market:
   • "For any future date D (from 2023 to 2033), predict the total market capitalization of any subset of cryptocurrencies on that date, conditioning on the S&P 500 and other global economic indicators."
3. Political Forecasting:
   • "For each year from 2024 to 2100, predict the joint density of the party of the president, the number of House Representatives of each party, the number of Senate Representatives of each party, and the number of Supreme Court justices of each party."
4. Demographic Predictions:
   • "For any future year T (2025 to 2100) and country, predict the life expectancy and other parameters that will be reported by Our World in Data for that year and region."
5. Geopolitical Risk Assessment:
   • "Conditional on US-Russia tensions (as measured by the Geopolitical Threat Index) being X at a time T in the future, what will the Metaculus forecast be for 'Chance of nuclear weapon use before 2030' on time Y?"
6. Medical Forecasting:
   • "Given an individual with demographic information D, predict their probability of developing a medical condition M by point in time T."

These examples highlight the flexibility and potential of scorable functions across various domains. It took significant experimentation to identify suitable questions for current prediction tournaments and markets. With the introduction of scorable functions, the range of possibilities expands dramatically, requiring time and experimentation to fully understand and optimize their use.

How Scorable Function Forecasting Tournaments Could Work

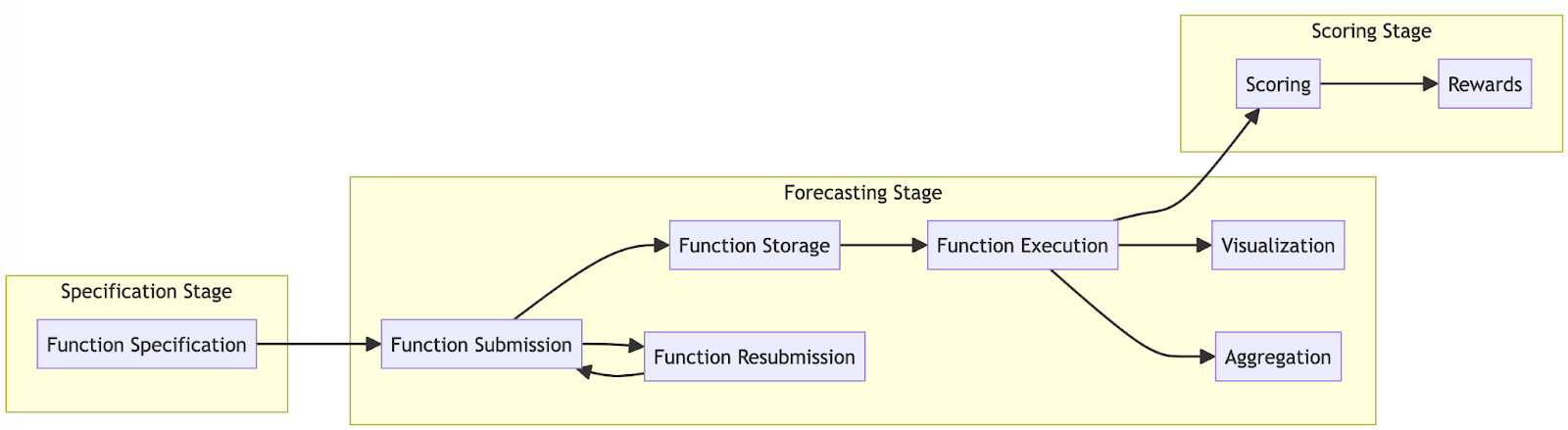
The key idea is to generalize prediction markets to support forecasts in the form of scorable functions. Here's a rough sketch of how a tournament using scorable functions could work.

1. Function Specification: Questions specify a precise function specification for forecasts. For example, "Submit a function that predicts a probability distribution of the US inflation rate (Y), given the Fed funds rate and unemployment rate (X1, X2), for any given month from Jan 2024 to Dec 2026."
2. Submission of Code: Forecasters submit actual code (e.g., Python functions, Squiggle functions) matching that specification. These can range from simple models to sophisticated machine learning models.
3. Storage and Evaluation: Scorable functions are stored and managed by the platform, evaluated programmatically to generate up-to-date forecasts. Forecasters can submit updated versions of their functions as needed.
4. Visualization: The platform provides tools to aggregate scorable functions, visualize their outputs, and analyze their performance over time.
5. Scoring and Payouts: At the end of the forecasting period, all versions of the scorable functions are scored using pre-specified metrics (e.g., Brier score, log loss). Payouts are allocated based on performance.

Scorable Function Forecasting vs. Traditional Statistical Modeling

Scorable function forecasting and traditional statistical modeling both aim to make quantitative predictions but differ in several key aspects.

1. Model Scope and Modularity
   1. Traditional Statistical Models: Often comprehensive, modeling an entire system or process in one model.
   2. Scorable Functions: Modular and focused, with many small functions modeling individual components or relationships.
2. Model Development and Ownership:
   1. Traditional Statistical Models: Developed by individual organizations for specific use cases, often requiring custom infrastructure.
   2. Scorable Functions: Uses common platforms for many models. Open and collaborative, allowing multiple users to define, submit, and update models.
3. Approach and Emphasis:
   1. Traditional Statistical Models: Heavily reliant on historical data to identify patterns and make predictions.
   2. Scorable Functions: Combines data-driven and theory-driven approaches, incorporating both data and subjective judgment.
4. Model Lifecycle and Evaluation:
   1. Traditional Statistical Models: Often developed, trained, and deployed for a specific period. Outputs and scoring methods are highly customized for the model type.
   2. Scorable Functions: Models are continually updated and evaluated over longer time horizons. There’s an emphasis on a few common mode outputs and scoring methods.

The modular nature of scorable functions is a significant advantage. It allows for the creation of many small, focused functions that model specific components or relationships. These functions can be easily combined and reused in different contexts. For example:

average_salary(minAge, maxAge, profession) ... // returns average salary based on age range and profession

remaining_working_life_years(age, gender) = ... // simple model of working years

remaining_lifetime_earnings(age, gender, profession) = {
   remaining_years = remaining_working_life_years(age, gender)
   remaining_years * average_salary(age, age + remaining_years, profession)
}

In this example, remaining_working_life and average_salary are small, modular scorable functions that can be used independently or combined to create a more complex function like remaining_lifetime_earnings. This kind of modularity and reusability is not typically emphasized in traditional statistical models.

The main downside of scorable functions compared to traditional statistical models is the need for custom high-level infrastructure. The increased generality requires standardization, which can incur substantial costs. Whether this approach is worth it depends on the specific needs at hand.

Examples of Specialized Scorable Function Platforms

Several platforms have implemented specialized versions of scorable functions:

• Kaggle Competitions: Participants submit models (often in Python or R) that are run against a hidden test dataset to generate predictions, scored to determine a leaderboard.
• Numerai: A hedge fund that crowdsources its trading models through weekly tournaments, with data scientists submitting prediction models that are scored on live data.
• Quantopian (now defunct): Allowed users to submit algorithmic trading strategies in Python that could be backtested and live-traded.
• Insurance Industry: Actuarial models estimate claim probabilities and severities, developed in languages like APL, SAS, R, or Python.

These demonstrate some of the potential of this approach, but these platforms haven’t yet allowed for generic forecasting on future questions.

Challenges for Forecasters

Writing functions is more complicated than submitting point probability or single distribution forecasts but is within the realm of people with some programming experience. The complexity of function specifications can vary widely, from simple models to advanced ones.

Note that:

1. Right now very few people have experience writing models by hand, using mostly intuition instead of statistics. Once people get over the initial learning curve, the marginal work of the programming element might be pretty low. It should get a lot intimidating with a bit of practice.
2. In a forecasting team, only some people need to be responsible for the algorithms. Most team members can do other things. In a forecasting ecosystem, it can be beneficial if even a small amount is dedicated to these sorts of models.
3. AI is getting better quickly. It’s already helping Squiggle users write code. That should help a lot in writing these algorithms.

Challenges for Forecasting Platforms

Creating general domain forecasting platforms with support for scorable functions presents numerous challenges. However, with clever engineering, these obstacles can be achievable. For instance, Squiggle Hub provides a minimal but promising example of this concept in action, with further developments to be announced.

The level of support for scorable functions can vary widely. Supporting small functions in a single language with limited function definitions can be relatively straightforward. However, implementing comprehensive support for a wide range of features and properties is more complex.

Potential challenges and features include:

• Continuous Model Updating and Scoring: Ensuring that models are continuously updated and accurately scored in real-time.
• Interoperability: Facilitating easy function calls between different scorable functions.
• Integration with Libraries and APIs: Allowing seamless integration with external libraries, data sources, and APIs.
• Leveraging AI: Enabling scorable functions to call large language models (LLMs).
• Multilingual Support: Integrating multiple programming languages to accommodate diverse user preferences.
• Sophisticated Tournament Structures: Designing highly-variable and sophisticated tournament structures and reward functions.
• Cost Management: Handling financial costs, especially when functions are expensive to run.
• Strong DSLs or APIs: Developing strong domain-specific languages (DSLs) or APIs for function specifications, implementations, and forecasts. This could enable an ecosystem of higher-order scorable functions, capable of estimating the calibration or computation costs of other functions.
• Performance Optimization: Ensuring fast startup times and runtimes, even with large sets of scorable functions.
• Versatile Interfaces: Creating interfaces for scorable functions that support not just estimation but also optimization.
• Caching Mechanisms: Implementing sophisticated caching mechanisms to quickly approximate slow functions.
• User-Friendly Tools: Developing solid user interfaces, plots, and diagrams for various scorable function definitions and scoring methods.

In practice, few platforms will likely have many of those features anytime soon. The place to begin is probably with minimal implementations that allow for early experimentation. But later on, there is a very high ceiling for great scorable function platforms.

Conclusion

Scorable functions represent a potential advancement in forecasting tournaments, combining the precision of algorithmic models with the domain generality of judgemental forecasting platforms. The main ideas are fairly simple. Now there’s a lot of work to do to both build up the necessary technical capabilities and begin experimenting with them.

Appendix: Key Terminology

Prediction Market: A speculative market where participants trade contracts based on the outcome of uncertain future events. The prices in a prediction market can indicate what the crowd thinks the probability of the event is.

Prediction Tournament: A competition where participants make forecasts about future events or outcomes. These tournaments evaluate the accuracy and calibration of the forecasts, rewarding the best performers. Similar to prediction markets, they apply specific formats to questions across various topics and feature competition among many participants.

Scorable Function: An executable model that returns probabilistic predictions and can be directly evaluated and scored through function calls. Scorable functions encapsulate forecasting logic, which can be based on human intuition, statistical analysis, or a combination of both. They are a subset of regular programming functions.

Traditional Statistical Model: Conventional models used for forecasting that often involve comprehensive, data-driven approaches to represent entire systems or processes. These models are typically developed by individual organizations for specific use cases, require custom infrastructure, and heavily rely on historical data to identify patterns and make predictions.

Model: In the context of forecasting, a model is any method or algorithm that converts inputs into specific estimates or predictions. Both statistical models and scorable functions are types of models.

Bot: An automated program that performs tasks, such as submitting forecasts or updating predictions based on predefined algorithms. In forecasting platforms, bots can automate the process of making and adjusting predictions. A bot can use a model internally but is not itself a scorable function or a model.

Algorithmic Forecasting: The use of algorithms to analyze data and make predictions about future events. This can involve the use of bots, statistical models, and scorable functions.

Thanks to everyone who has helped on QURI on this topic so far. Also, thanks to Anthropic and Claude 3, which helped a lot with this post.