Further evidence for what you show in this post, is the plot of the kurtosis of the activation vectors with varying dropout. Using kurtosis to measure the presence of a privileged basis is introduced in Privileged Bases in the Transformer Residual Stream. Activations in a non-privileged basis should be from a distribution with kurtosis ~3 (isotropic gaussian).
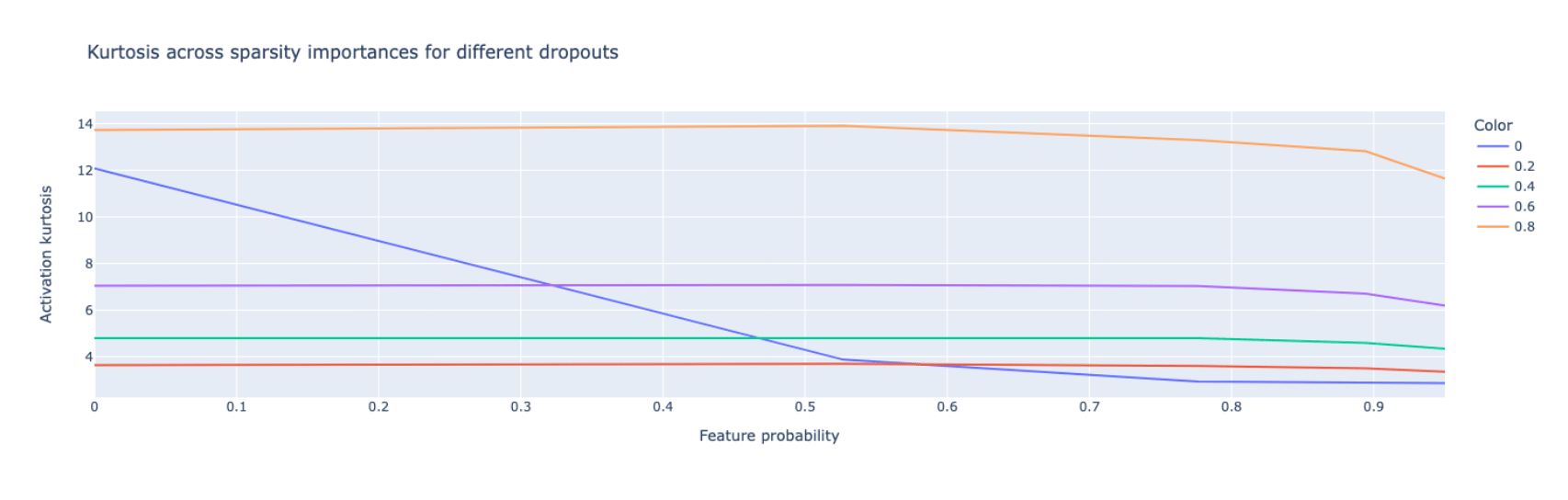
With a higher dropout, you also get a higher kurtosis, which implies a heavier tailed distribution of activations.
Cool post! I have done some similar work, and my hypothesis for why dropout may inhibit superposition is that spreading out feature representations across multiple neurons exposes them to a higher chance of being perturbed. If we have a feature represented across neurons, with dropout , the chance that the feature does not get perturbed at all is .
I think that dropout inhibits superposition is pretty intuitive; there's a sense in which superposition seems like a 'delicate' phenomenon and adding random noise obviously increases the noise floor of what the model can represent. It might be possible to make some more quantitative predictions about this in the ReLU output model which would be cool, though maybe not that important relative to doing more on the effect of dropout/superposition in more realistic models.
Abstract
This post summarises some interesting results on dropout in the ReLU output model. The ReLU output model, introduced here is a minimal toy model of a neural network which can exhibit features being in 'superposition', rather than a single 'neuron' (dimension) being devoted to each feature. This post explores what effects dropout has on the alignment of the basis in an otherwise rotation invariant model.
This particular question was listed on Neel Nanda's 'Concrete problems in mechanistic interpretability' Sequence. I work in machine learning and while I've always thought that mech-interp was an interesting direction, it seems particularly more urgent recently for reasons which I think will be clear to anyone reading LW. I originally started playing with this question because I was considering applying to this ; I no longer think I will do so this year for personal reasons, but I thought that my results were interesting enough to be worth writing up. I have never posted on LW before, but as the concrete problems list was posted here I thought it was a better place to publish a write-up, rather than my personal blog which I don't think gets very much visibility.[1]
Introduction
The ReLU output model is a very simple model of a mapping from neural network 'features' to concrete 'hidden dimensions', which can exhibit superposition. The model is as follows, for a vector of 'features' x∈Rn and a hidden vector h∈Rm, with n>>m.
h=Wxx′=ReLU(WTh+b)
This model is of interest as an extremely simple test case of how a model can represent a large set of (hypothetical) disentangled 'features' in a much lower dimensional vector space by placing those vectors into 'superposition'. This model, and observations of superpositions in it, were first introduced and studied in this article.
This model is rotation invariant in the sense that W can apply an orthonormal matrix O to the weights without changing anything; x′=ReLU(WTOTh+b)=ReLU(WTOTOWx+b)=ReLU(WTWx+b). Problem 4.1 on Nanda's 'Concrete Problems' sequence asks whether dropout breaks this symmetry and introduces a privileged basis in this model.
We can define a ReLU dropout model; h=Wxh′=dropout(h,r)x′=ReLU(WTh′+b) where r is the dropout rate; that is, the elements of the hidden variable h are uniformly set to zero with probability r.
In this post, I present some empirical observations that dropout can create a privileged basis in the ReLU output model. In fact the observed behaviour is fairly complex, with at least 3 regimes depending on the dropout rate. This suggests that dropout may have a nontrivial interaction with methods designed to induce mechanistic interpretability, and this perhaps deserves some more research. I also show some results on the effect of dropout on superposition, which is less conclusive but still kind of interesting.
Results
Using sparse features as in the toy models paper, we can make all the feature importances the same. [2] This means that as all the features are identical, we can choose a single feature arbitrarily to determine the 'orientation' of the hidden layer basis; for instance, we can define the orientation of the co-ordinate basis as the feature vector with the largest norm (this makes sure that we choose a feature which is actually represented).
That is, given the weight matrix W of the ReLU output model, we consider the list of row vectors W0,W1,W2,...Wn of W. We calculate the norms of all of these, and choose the row Wmax with the maximum vector norm to define the 'orientation' of our basis. We then consider the unit vector u=Wmax||Wmax|| as defining the 'orientation' of the basis. As we have features of equal importance, choosing the max norm feature means that we choose more or less randomly among features the model chooses to represent.
We can check that this method is reasonable by first visualising the distribution of u for a large sample of non-dropout ReLU output models. We will start with 2d models, as this let's us visualise u easily in 2d. As we expect, we see that the distribution of u is uniform on the unit circle - there is no preferred orientation of the learned hidden basis.
The simplest thing to try, then, is to increase dropout rates, and see if we observe any changes to the distribution. The following graph figure shows this. To make it easier to tell the different dropout rates apart, as well as colouring the scatter plot, I've multiplied the size of the unit vectors by 1+2∗r where r is the dropout rate so that the circle's the unit vectors are distributed on do not overlap. This shows the behaviour for a fairly low feature probability of 0.2 (i.e sparse features)
As we can see, introducing dropout certainly has an effect on the distribution of the orientation of the basis! In addition, the effect is suprisingly complicated; I think when I started messing around with this, I expected dropout to either have little effect or to bias the model to avoid the co-ordinate basis. Instead, we see a few distinct phases; low levels of dropout bias the model towards avoiding the co-ordinate basis, and at higher levels (>50% ) dropout rate the model seems to become aligned with the co-ordinate basis. This seems to show that dropout can introduce a privileged basis, and not only that, but this privileged basis can align with the co-ordinate basis.
Interestingly, this effect seems either go away or be much less important with dense features:
It's not clear to me why this is.
It's slightly harder to visualise this in high dimensions, but again we can exploit the symmetry of the equal feature importance case to help; in this case, if the features are uniformly distributed, then we would expect u to lie on the surface of a unit hypersphere. By plotting any two feature dimensions, we can take slice through this hypersphere. Again, at high sparsity levels, we see the clear emergence of axis alignment.
We can see the emergence of axis-alignment directly in the weights too (holding sparsity constant, increasing dropout rate, plotting W only:
Again, the axis alignment only seems to happen for high dropout rates of over ~50%.
Nevertheless, this is clear evidence that in certain circumstances, dropout can induce a privileged basis in otherwise rotation invariant models. This is potentially quite important for interpretability work on transformers, which sometimes use dropout in places where there is otherwise no mechanism to induce a privileged basis or align the features with the 'neurons' such as after the self-attention layer.
Dropout and Superposition.
As well as having some effect on the preferred basis of the weights, dropout has a non-trivial effect on the superposition learned by a ReLU output model.
This shows the feature by feature matrix (WTW) for various values of dropout (increasing dropout from top to bottom) and feature sparsity (increasing sparsity across the x axis). Dropout has a clear qualitative effect on the superposition learned by the model, but the exact effect is quite difficult to quantify; generally, I think dropout inhibits superposition.
We can try to get a better idea by visualising the 'dimensions per feature' as a function of sparsity for various dropout levels. This does seem to back up the general trend that dropout inhibits superposition, with models with more dropout having higher dimensions per feature for a given sparsity rate, but this effect is not strict; at low levels of dropout and certain sparsity, the dimensions per feature can be lower for dropout models; it seems to me that dropout makes some of the 'sticky' configurations observed in the anthropic post less attractive to the model? I don't really have a good theory for what might cause this; this might be interesting to explore in further work.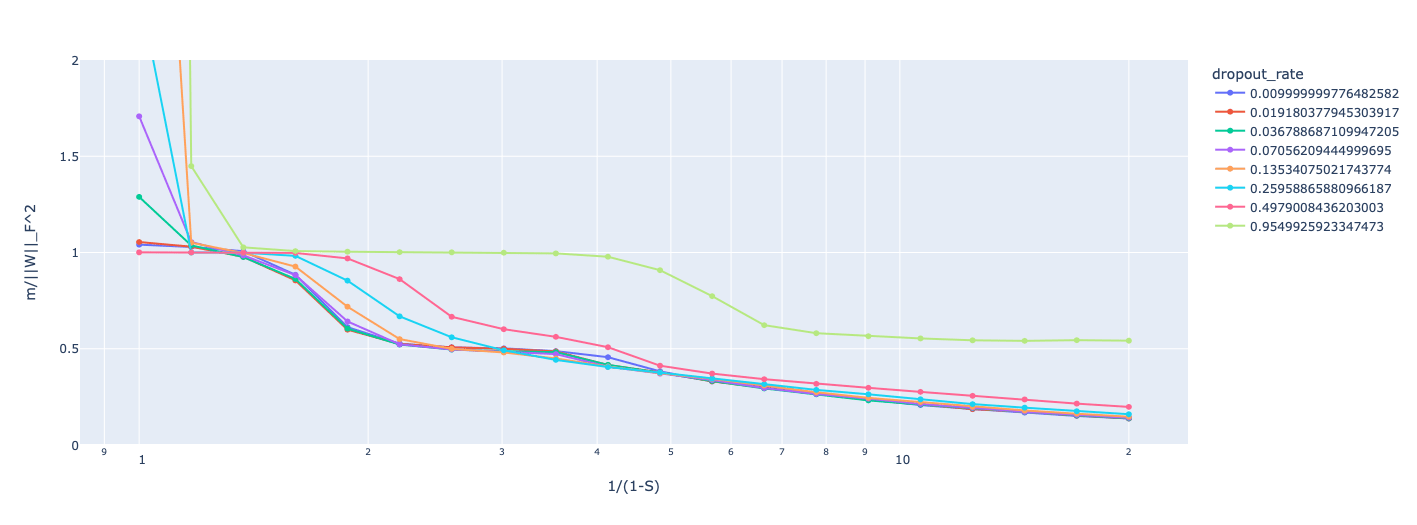
also the markdown editor is actually really good! ↩︎
This is an extremely simple case in a simplified model, but we only need to find a single example of dropout causing a privileged basis to prove that it's worth consideration. ↩︎