Abstract - What this essay does and does not cover

This essay attempts a resolution to Newcomb’s problem in the case of a perfect predictor (aka limit case). The essay does give a solution, but the goal of this essay is more ambitious.

The goal is that a supporter of 1-boxing, a supporter of 2-boxing, and any undecided people would all unanimously come to an agreement with the conclusion of this essay (if they read it through and follow the argument). To that end, separate sections “Focusing on the source of confusion in Newcomb’s Problem with Perfect Predictor” and a section of illustrative examples are given . However, this essay follows a chronological order and skipping any section, besides the introduction and the final section with illustrative examples, is unadvised.

I argue that in the perfect predictor case, the apparent disagreement between 1-boxers and 2-boxers emerges from an incorrect placement of the decision node of the agent. The classical framing of the problem conflates a deterministic execution node with a decision node. Once this is recognized the source of the disagreement between 1-boxers and 2-boxers is dissolved.

After reading this essay, there are still two questions where readers might disagree. They are as follows:

1. Do humans have absolute free will?
2. Can humans voluntarily choose what to believe and what not to believe?

These are relevant questions. However, they are not questions about decision theory. They do not deal with maximization of utility under set circumstances. This essay aims to resolve Newcomb’s problem with a perfect predictor as a decision theory problem. If the reader finds that this essay has reduced the problem from a decision theory problem to a problem entirely about free will and belief formation, then I shall consider the aim of this essay to have been accomplished.

Introduction

While Newcomb’s problem is widely known, it is still helpful to look at the exact statement of the problem to make sure we are on the same page.

Let’s consider the version from Newcomb’s Problem and Regret of Rationality

A superintelligence from another galaxy, whom we shall call Omega, comes to Earth and sets about playing a strange little game.  In this game, Omega selects a human being, sets down two boxes in front of them, and flies away.

Box A is transparent and contains a thousand dollars.

Box B is opaque, and contains either a million dollars, or nothing.

You can take both boxes, or take only box B.

And the twist is that Omega has put a million dollars in box B iff Omega has predicted that you will take only box B.

Omega has been correct on each of 100 observed occasions so far - everyone who took both boxes has found box B empty and received only a thousand dollars; everyone who took only box B has found B containing a million dollars.  (We assume that box A vanishes in a puff of smoke if you take only box B; no one else can take box A afterward.)

Before you make your choice, Omega has flown off and moved on to its next game.  Box B is already empty or already full.

Omega drops two boxes on the ground in front of you and flies off.

Do you take both boxes, or only box B?

I shall focus on a special case (known as the limit case) where the predictor (Omega) is not just very good at predicting but infallible. This is considered an important version because you can set the probability of the predictor being correct arbitrarily high in the original without changing the nature of the problem.

There are several approaches to this problem taken by different decision theories. Notable among them are the following:

1. Causal Decision Theory (basically what most people think of when the hear decision theory) supports 2-boxing
2. Updateless Decision Theory and Evidential Decision Theory supports 1-boxing.

This essay doesn’t present a new decision theory, but tries to isolate and resolve the source of disagreement between the 1-boxing and 2-boxing decision theorists.

Simplified Variants as Intuition Pumps

Consider Newcomb’s Problem, but with a difference. You are asked to write a computer program that chooses whether to 1-box or 2-box. Since this is a computer program, we don’t need an omniscient predictor (or alien Omega) to predict what the code would do. A human computer programmer would read your code after you submit it and decide whether your program chooses 1-boxing or 2-boxing. Then the code reader would assign money in two boxes based on the predicted output of your code, just like Omega does in the original problem. The computer programmer is really good and doesn’t make a mistake in reading the code. Whichever option your code picks, you will receive the money corresponding to that outcome.

Let’s call this situation Newcomb v2.0

Decision theorists that support 1-boxing in the original Newcomb problem and those that support 2-boxing, would both agree on a single solution for Newcomb v2.0. Submit a program that 1-boxes.

There is no conflict between the 1-boxers and 2-boxers in Newcomb v2.0. They agree.

Now, let’s consider another modification to the problem. The code you submit would not face a single problem. It would face a series of problems with 2 options, choosing one box or two boxes. But some of these problems would have monetary amounts assigned between the two boxes according to the prediction by the human reading the code and some other cases would have amounts assigned to the two boxes at random.

But the code would be allowed to take an input in each case before giving a solution. If the boxes have amounts assigned by the human code reader, like Newcomb 2.0, then a binary variable RetroCausality is assigned the value True. If the amounts are assigned at random then the variable RetroCausality would be assigned value False.

Let’s call this problem Newcomb v3.0

Again the people who in the original version of the problem were divided between 1-boxing and 2-boxing, can come to an agreement here. Submit the code according to the following algorithm:

If RetroCausality == True:

print(“I will 1-box”)

Else:                                        # if RetroCausality == False

print(“I will 2 box”)

There is no disagreement between 1-boxers and 2-boxers in Newcomb v3.0. They agree.

Now, let’s consider just one more variation. You are in the Newcomb v3.0 situation with your code ready, waiting for someone to come and collect it and run the simulation. But then the human checker walks in and says, “We are very sorry but our computer systems have a virus, we can’t compile any code you give. But we have a solution. We need you to give me the code and then sit in a chair facing a screen and a key pad with two keys named 1-box and 2-box. The screen would show one line of text at any time saying either “RetroCausality = True” or “RetroCausality = False”. Since you wrote your code, you can predict what your code would have done for each scenario. We would need you to push the button 1-box or the button 2-box accordingly. After you press either button the line on the screen would refresh and you would need to press another button. This would continue till we have run N number of simulations. I would be reading your code and verifying that you pressed the same buttons that your code would have chosen. If there is any discrepancy between what you choose and what your code would have chosen, then we would need you to repeat the process again from the beginning.”

Let’s call this situation Newcomb v4.0

Again, the 1-boxers and 2-boxers of the original problem agree on the solution of Newcomb v4.0. Submit the code similar to the solution of Newcomb v3.0 and press the buttons accordingly.

There is no disagreement between 1-boxers and 2-boxers in Newcomb v4.0. They agree.

Decision Node Placement in Newcomb's Problem with Perfect Predictor

The disagreement between 1-boxers and 2-boxers in the original version of Newcomb’s problem emerges due to an incorrect placement of the decision node.

A decision node is when a decision is made, not when a previously made decision is physically carried out.

If the person is making a physical movement, but the movement has been uniquely determined at a prior time, then the current point is not a decision node, it is a deterministic execution node. The prior point when the decision was determined was the decision node. The fact that the person might think they are making a fresh decision does not change this situation (more on this later).

Along these lines, I suggest a new rule to be applied to all decision theory problems. It may be stated informally as follows:

In a decision theory (or game theory) problem, if an agent ever crosses a point (let’s call it determinism point) such that all their later actions are perfectly determined, then that agent should not have any decision node downstream from that point. The agent can have decision nodes in the decision tree but they should be exclusively limited to the region upstream of the determinism point. After the determinism point, the entity that was an agent would be treated as a part of the environment and no longer as an agent.

The determinism point might be limiting the agent’s actions by unbreakable pre-commitment or by the laws of physics themselves. The method is not important.

Using the above rule to limit decision node placement removes all retrocausality from decision theory problems, allowing us to study the same problem with the methods used in classical decision theory.

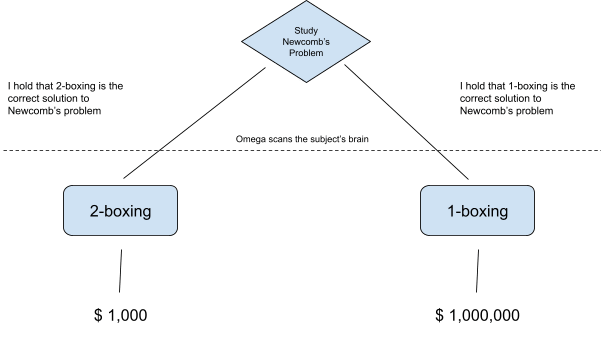
In Newcomb’s original problem, the decision node is not when the person has two boxes in front of them. The decision node is at a point before their brain is scanned by Omega. More specifically, it is the last time they thought about retrocausality before their brain was scanned and decided whether or not they strictly follow causal decision theory.

Consider the following decision tree:

The action of 1-boxing or 2-boxing after the boxes are presented to you is a deterministic execution node, it is not a decision node. There was a decision node, but it was the last time you thought about Newcomb’s problem before your brain was scanned (or whatever other technique was used by Omega to predict your actions).

Of course, it doesn’t need to be exactly Newcomb’s problem that you studied. It might be any other problem of decision theory that has a similar feature. What matters is that choosing a particular strategy in any problem involving retrocausality uniquely determines whether you strictly follow causal decision theory or not. If you think one option (either or them) makes more sense in any such problem, that is equivalent to making a decision in all of them.

It might not even have been about decision theory explicitly. If you decided that being rational meant winning more resources, then that means you also decided to 1-box in Newcomb’s problem even if you haven’t even heard of it.

You might not see how saying “rationality is about winning, and I follow rationality” is sufficient to imply “I will 1-box in Newcomb’s problem”. But the conceptual chain linking them exists and it is strong.

The decision node was before your brain was scanned; the last time you thought about Newcomb’s problem (or some other similar problem involving retrocausality) and decided whether you would 1-box or 2-box.

Now for the big paradox. What if you say to yourself, “I hold that 1-boxing is the correct solution to Newcomb’s problem, I don’t strictly follow causal decision theory!”. But when Omega presents the two boxes then you choose 2-boxing! Would you then get $ 1,001,000?

No. Here we need to understand the difference between believing in something versus believing in belief.

Consider the following pseudo-code:

If facing(question(“What would you do in Newcomb’s problem?”)):

print(“I will 1-box”)

If facing(Newcomb’s problem):

print(“I will 2-box”)

If a human code reader has to read the above pseudo-code and decide whether or not to put money in the second box based on whether the algorithm is a 1-boxer or 2-boxer, then they would easily realize that the algorithm is a 2-boxer. Thus, they would leave the second box empty.

Remember, Omega doesn’t just ask you what you believe in, he scans your entire brain. You can’t hide any if-statements from Omega.

To believe that 1-boxing is the objectively correct solution to the problem, you have to believe in it as a law of nature, like relativity. Yes, if a huge mass of fresh counter evidence is presented to me, I can even give up my belief in relativity. But only after fresh hard evidence is presented. I can’t just stop believing in relativity because I think doing so will give me another $ 1,000.

If you do not strictly follow causal decision theory, if you believe 1-boxing is the correct solution, then you will 1-box. You can change your mind if you find a logical flaw in the argument or some new counter evidence. But in the absence of either a logical flaw or counter evidence, you can’t just stop believing it because that would give you an additional $ 1,000.

If you profess your belief in a decision theoretic solution but then act in a way that violates it, even though you haven’t encountered any new evidence in the meantime to challenge your belief, then you didn’t ever believe in it in the first place. In this case you reach for both the boxes but get only $ 1,000.

Similarly, you can be someone who has studied causal decision theory and find yourself saying, “I would 2-box in Newcomb’s problem”. But somewhere in your mind you aren’t convinced. So when you find yourself really facing the problem, you choose to 1-box.

Again, you believed that you believe 2-boxing is the right solution. But actually you believed 1-boxing was the solution all along.

So for the human reader planning to get $ 1,001,000, the question you should really be asking is, “Can I deliberately and consciously choose to believe or disbelieve particular ideas?”

This is a valid question, but it is a question of doxastic agency; not a question of decision theory.

My Solution to the Problem

The solution I am giving is as follows:

1. If you are on the decision node before the scan, and have the ability to perfectly control the source code of the agent (might be yourself), then adjust the agent's source code to 1-box.
2. If you are downstream from the scan, then the question "what decision should you make?" is meaningless because you do not have a decision node. You will just do whatever your source code says. At this point you are a part of the environment of the game and not an agent (even though you might mistakenly feel like you are an agent).
3. If you are on the decision node before the scan, but you can't perfectly control the source code of the agent, then try your best to get the agent to 1-box.

Try to convince yourself (and others) to 1-box as well as you can, but don't be surprised if they 2-box because we can't just edit the source code of humans (not with the current knowledge of neuroscience). Not even if we ourselves are that human and we really want to make ourselves commit to 1-boxing.

Focusing on the Source of Confusion in Newcomb's Problem with Perfect Predictor

When a person tries to think of Newcomb’s problem, they try to simulate the situation in their imagination. Most of the confusion surrounding Newcomb’s problem does not come from a confusion about decision theory. It comes from trying to hold two contradictory statements as simultaneously true in your imagination.

Let’s consider a trivial version of the problem that doesn’t have any omniscient being predicting your behavior. What if someone comes to you and offers the two boxes but without any attempt to predict your behavior. Traditional 1-boxers and 2-boxers would both agree that the correct response in this situation is to 2-box. Let’s call this Newcomb’s problem vTrivial.

Similarly in Newcomb’s problem v2.0 and v3.0 when the human was replaced by a computer program, again traditional 1-boxers and 2-boxers would both agree that the question “What should the code do?” is a meaningless question. It is a computer code, it will do what it has been designed to do. That is to say it is not an agent with a decision node, it is a part of the environment at a deterministic execution node.

Similarly, if we allow for the possibility of a person writing the code before it is read by the human who sets up the two boxes, then again traditional 1-boxers and 2-boxers would agree that the correct action for the code-writer is to submit a code that 1-boxes in Newcomb’s problem.

There is agreement between 1-boxers and 2-boxers in all these three cases because they agree on the following aspects of these problems:

1. In Newcomb’s problem vTrivial the human is allowed to choose whatever they want. They are not a deterministic entity (there is a decision node at that point).
2. In Newcomb’s problem v2.0 and v3.0, it makes no sense to ask “What should the code do?”. It is a code, i.e. a deterministic agent (there is no decision node at that point).
3. In Newcomb’s problem v2.0 and v3.0, the human should write a 1-boxing code before submitting it to the reader. The code-writer is not deterministic, but their decision node is before the code is submitted, afterwards they don’t have a decision node in the game.

The apparent confusion in the original Newcomb’s problem comes from trying to simultaneously hold the following two statements as true:

1. At the point when the boxes are presented, the agent has a decision node, i.e. the ability to make a decision (similar to Newcomb’s problem vTrivial) not just physically carry out a previously made decision.
2. At the point when the boxes are presented, the agent doesn’t have a decision node. They are just carrying out a decision previously determined. They are a deterministic element of the problem instead of an agent (similar to Newcomb’s v2.0 and v3.0).

These two statements are mutually exclusive. Both of them can not be true at the same time. Hence the confusion in trying to simulate Newcomb’s problem in your imagination.

One can imagine a red chair or a black chair, or a chair that has both red and black patches, or a chair whose color is the average between red and black, or one whose color fluctuates between red and black. But one can not imagine a chair that is entirely red and entirely black at the same time. Any attempt to do so would only lead to mental confusion.

The traditional supporters of the 1-boxing and 2-boxing strategies would all agree on the solutions of Newcomb’s problem v2.0, v3.0, v4.0, and vTrivial; because these versions clearly specify whether the agent does or does not have a decision node after the boxes are presented.

How is this Formulation Different from Existing Theories?

What has been attempted here is a resolution instead of a solution advising 1-boxing or 2-boxing. No new Decision Theory has been created. However, it may be important to note how this formulation is different from any of the existing decision theories.

There are existing decision theories that recommend 1-boxing. Most notably Updateless Decision Theory and Evidential Decision Theory. In versions where they deal with AI the solutions are similar to my recommendations. In human agent versions, they advice to pre-commit to 1-boxing. This might seem similar to the solution being presented here but there is a significant difference.

I am not advising pre-commitment. I am stating that if a perfect predictor exists (like Omega) then the decision maker physically does not have free will to make a decision after passing through a determinism point. It is not a voluntary commitment maintained by will power. It is an unbreakable commitment held by the laws of physics. This doesn't mean there is no free will in general, just that the agent doesn't have free will after the scan.

I am not just recommending pre-commitment, I am postulating the collapse of downstream agency under perfect prediction.

And if humans have absolute free will all the time, then a perfect predictor of humans can not exist. In that case, the perfect predictor version of the problem doesn't make sense.

However, we know that perfect predictors of some types of agents do exist. If the agent is a computer code then any human who knows coding, and given enough time, can perfectly predict the future outputs of the code, especially if it is a simple code (not including pseudo-random number generators, which also can be predicted with a bit of extra knowledge). Note, we are talking about a piece of computer code, not an AI architecture.

Decision theory is about what option should an agent choose at a decision node to maximize utility. The recommendations should not change based on whether the agent is a human, any other animal, a robot, an alien, or a sentient shade of the color blue.

If we consider a computer code to be the agent and a human code reader to be the perfect predictor in Newcomb’s problem, then the problem resolves itself. The code will do whatever it has been designed to do. What decision the code should make is a meaningless question.

This can be better understood if we return to the example of Newcomb’s problem v2.0, v3.0, and v4.0. You might find it difficult to visualize a human without free will, but by replacing the person with a code (written by the person), we make it easier to visualize the fact that the decision made is the decision before you write the code (before your brain is scanned). You can’t interfere in the running of the code, you just get to write the code before submitting it.

If you still feel confused about Newcomb’s problem as a decision theory problem, then try to phrase the same confusion but with the human agent replaced by a piece of code and Omega replaced by a human code reader (like Newcomb’s v3.0). Does the confusion still hold?

Illustrative Examples

I know there will still be some doubt in your mind. That is because there is a difference between answering a question and explaining away a confusion. To do the latter, you can’t just give the correct answer, you have to explain why the other answers are incorrect.

The different versions of Newcomb’s problem I mentioned before were an attempt to explain away the confusion, but now I would make a stronger attempt using a few different hypothetical situations.

First Scenario.

You are walking somewhere in your neighborhood, when suddenly a spaceship lands in front of you and Omega walks out. He explains to you the entire rules of Newcomb’s problem. When you expect him to present the two boxes, instead of doing that he says, “Today, I came to your planet and was about to scan your brain but guess what? The brain scanning machine isn’t working! Now, I really want to get this done and move on to the next solar system, so can you just tell me whether you are a 1-boxer or 2-boxer? And I am tired of putting money in the boxes. If you say 1-boxer, then I would just give you the $ 1,000,000 and if you say 2-boxer then I will give you $ 1,000. I would be moving on and never returning to your solar system, so technically you can lie and I would never know. But still let’s get this done.”

You remember that you are friends with two decision theorists, one of them a 1-boxer and the other a 2-boxer. You ask Omega, “I am sorry, but I was just about to call two of my friends when you landed. Do you mind if I do that first?”

Omega says, “Sure. Go ahead, but don’t take the entire day.”

You call one of your decision theorist friends, or both of them, or take them both on a simultaneous conference call, that part doesn’t matter. You explain the entire situation to them including the dysfunctional brain scanning machine.

In this case both of your friends will give you the same advice. Tell Omega you are a 1-boxer and take the $ 1,000,000.

They both agree.

Second scenario.

Omega is done explaining the rules of Newcomb’s problem to you. But then instead of pulling out two boxes he says, “My brain scanning machine isn’t working right now. So can you just tell me whether you are a 1-boxer or 2-boxer? I would drop the boxes here and leave. I would be moving on and never returning to your solar system, so technically you can lie and I would never know. But let’s get this done.”

You remember that you are friends with two decision theorists, one of them a 1-boxer and the other a 2-boxer. You ask Omega, “I am sorry, but I was just about to call two of my friends when you landed. Do you mind if I do that first?”

Omega says, “Sure. Go ahead.”

You call one of your decision theorist friends. You explain the entire situation to them including the dysfunctional brain scanning machine.

In this case also both of your friends will give you the same advice. Tell Omega you are a 1-boxer, but then 2-box after Omega leaves. That will give you $ 1,001,000.

They both agree.

Third scenario

Omega lands before you and explains everything. Then he says, “So I scanned your brain and then I found that my Surrounding Influence Scanner machine wasn’t working. So I know exactly what decision you would make on your own, but I don’t know what decision you would make if you were to come in contact with some new source of influence between the moment when I scanned your brain and the moment when you made a choice. If any external influence changes your decision that would not change the amounts of money I have assigned to the two boxes. The amount of money in the boxes is based only on your individual brain scan. Anyways here they are. I am off to the next solar system. Bye!”

You call your two decision theorist friends and explain the entire situation to them. They think for a moment but then they both come to an agreement.

“Do you trust us completely with the decision?” they ask.

“What do you mean?” you answer a question with another question.

“We mean are you going to listen to our advice and then do the opposite because you just wanted to hear what we had to say, or do you completely abdicate your decision making to us and promise to do what we say, regardless of what your intuition says?”

You think for a while. Then you reply, “I promise to do whatever you guys tell me to do if you can come to an agreement among yourselves.”

“And you are sure Omega said that his Surrounding Influence Scanner machine wasn’t working? He hadn’t scanned our brains, just yours?”

“Yes, he clarified that explicitly.”

Maybe the two of them ask you a few more things to ensure you are actually abdicating your decision making power to them. Eventually they are satisfied.

“2-box the problem” they say in unison.

You pick up the two boxes and open them. Either you become $ 1,000 richer or $ 1,001,000 richer. But in both cases you are sure your friends gave you the best answer. Nevertheless, curious as you are, you need to know how two people who disagree on the actual solution to Newcomb’s problem came to a unanimous decision now.

“How did you guys come to an agreement?” you ask your friends.

“By abdicating your decision making to us, you shifted the decision node to current time. In that case either both boxes had money or only one of them had money. In either case the correct solution is to 2-box. What you would have done if you had thought on your own is no longer relevant after you abdicate your decision making power to us; because there is no retrocausality in that case. Thus, 2-boxing was the only correct solution.”

They both agree.

Fourth Scenario.

You had never actually thought Newcomb’s problem would actually happen in reality, and that too to you!

You remember reading about it and thinking 1-boxing makes more sense. Yes, I believe 1-boxing is the only valid response to Newcomb’s problem.

Now the boxes sit in front of you. Omega is already thousands of miles away. What a weird guy!? But he is gone… he is gone. He can’t do anything now! You have always been a 1-boxer so he must have put money in both boxes. But what if now you pick both boxes?

You pick both the boxes, and then yell at the sky. $ 1,000?!? But why? Why? You have always believed in 1-boxing, this couldn’t be right.

You call your 1-boxer decision theorist friend and explain what happened.

“Yes” they say, “If you are a 2-boxer then you only get $ 1,000. That’s part of the problem.”

“But I am not a 2-boxer, I have always believed 1-boxing is the correct solution”

“That’s not how epistemic rationality works! It has to be empirical. You say that you are a 1-boxer. But whether you are a 1-boxer or 2-boxer isn’t determined by what you say. It is determined empirically! If you actually were a 1-boxer you would have picked 1 box. The fact that you 2-boxed, empirically proves you were a 2-boxer who only believed that they were a 1-boxer. Omega must have been able to see this in your brain scan. You didn’t believe it, you just believed that you believed in it.”

You want to tell your friend that they are wrong. That you were always a 1-boxer, as true as any! But then you realize something about this desire to counter your friend.

This internal voice sounds a lot like the voice that said “I believe 1-boxing is the solution to Newcomb’s problem”. You dig deeper into your volition and find something new. Empirical evidence does prove you were a 2-boxer. You want to counter your friend, but secretly you know they are right! You believe in believing that your friend is wrong, but you don’t actually believe it.

You take a deep breath and re-assess your beliefs. You make a commitment to yourself. If Omega gives you a second shot at the problem, you are going to 1-box no matter what other thoughts come into your mind.

Now, for the first time in your life, you are a true 1-boxer.

Final Scenario. Actual Newcomb’s Problem but you have read this article.

Omega has explained the rules to you. He places the two boxes in front of you.

Then he says, “I have scanned your brain. I have scanned everyone’s brain on your planet. I have scanned every piece of writing on your planet. In fact not just your planet, I have scanned the entire observable universe and every particle of it. I know whom you would talk to, I know what you would read, I know what the people and books will say, I know whether you will agree or not. I know what books will be written in the future. I know everything that will happen in your observable universe. There are no surprises for me. Anyways, got to go do the same thing in the next solar system. Bye!”

You see the spaceship vanish in the sky. For a few moments you think what a stupid thing to do for an omniscient being. You have omniscience and this is what you do with it?

Then you pull yourself back. There is a more immediate and personal decision to be made. The two boxes sit in front of you. Your two decision theorist friends’ number sits in your smartphone. Countless texts on decision theory sit on the internet and in libraries around the world.

You consider what to do now.

Perhaps you should call your friends. They will start arguing again, each certain how their answer is the correct answer. Perhaps more people will be called to weigh in. References will be pulled. Maybe even new books written to address the problem. You go through all the scenarios in your imagination, but none of them seems like it will give a convincing resolution.

And then you realize none of this matters.

What matters has already happened. A day several years ago when you read your last article about Newcomb’s problem. Or perhaps it wasn’t even about Newcomb’s problem but about some other problem involving retrocausality.

“That’s pretty clear” you had said to yourself. “I would ___”

And then you had said “1-box” or “2-box” or whatever were the equivalent options in that particular problem.

You remember that moment now, and suddenly you know exactly what’s inside the second box.